
- •Минобрнауки россии
- •1.Цель работы
- •2.Основные положения
- •2.1.Точность методов и результатов измерений
- •2.2. Погрешность и неопределенность результата измерений
- •2.3. Рекомендации по применению Руководства в метрологии
- •Процедура вычисления неопределенности
- •2.4.Сравнительный анализ двух подходов к выражению точности измерений
- •3. Пример. Измерение силы электрического тока с помощью
- •Уравнение измерений
- •5.А. По типу а вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер.
- •5.Б. По типу в вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющим систематический характер. Закон распределения величин внутри границ считают равномерным.
- •5.В. Суммарную стандартную неопределенность вычисляют по формуле
- •5. Тесты – задания для самоконтроля
- •6. Глоссарий (словарь терминов)
2.3. Рекомендации по применению Руководства в метрологии
Неопределенность измерения отражает тот факт, что для данного измерения имеется не единственное, а бесконечное число значений, рассеянных вокруг результата, который может быть обоснованно приписан измеряемой величине.
Числовые оценки неопределенности:
стандартная неопределенность uс
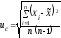 ,
(1)
,
(1)
характеризует дисперсию значений, которые можно обосновано приписать измеряемой величине;
расширенная неопределенность UР
UP = k uc, (2)
(k – коэффициент охвата)
определяет интервал значений, которые с достаточным основанием можно приписать измеряемой величине.
Категории неопределенности:
А – составляющие неопределенности, которые оцениваются статистическими методами;
В – составляющие, которые оцениваются другими способами.
Процедура вычисления неопределенности
Основа – «Руководство по выражению неопределенности измерений»
(Международный комитет мер и весов,
Международная организация по законодательной метрологии, Международная организация по стандартизации,
Международная электротехническая комиссия и др.)
введение поправок на известные систематические эффекты;
вычисление среднего арифметического каждой входной величины
(3)
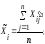
(
вычисление значения измеряемой величины:
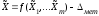 (4)
(4)
вычисление неопределенности по типу А:
стандартные неопределенности входных величин
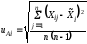 ; (5)
; (5)
суммарная стандартная неопределенность по типу А:
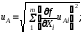 (6)
(6)
вычисление неопределенности по типу В:
стандартная неопределенность каждой входной величины
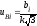 , (7)
, (7)
b – границы отклонения измеряемой величины;
k = 1,1 при доверительной вероятности Рд = 0,95;
суммарная стандартная неопределенность по типу В:
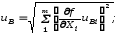 (8)
(8)
вычисление суммарной стандартной неопределенности
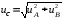 ; (9)
; (9)
вычисление расширенной неопределенности
UP = k uc , (10)
k =
tP(vе)
;
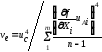 (11)
(11)
форма представления результата измерения:
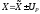 , uc
, k
, vе
. (12)
, uc
, k
, vе
. (12)
интерпретация полученных результатов:
интервал (
 )
содержит долю, равнуюРд,
распределения значений, которые могли
бы быть обоснованно приписаны измеряемой
величине.
)
содержит долю, равнуюРд,
распределения значений, которые могли
бы быть обоснованно приписаны измеряемой
величине.
2.4.Сравнительный анализ двух подходов к выражению точности измерений
1. Целью измерения является получение оценки истинного значения измеряемой величины, Понятие погрешности измерений, как разности между результатом измерений и истинным (действительным) значением измеряемой величины, используется для описания точности измерений в отечественных НД. Говоря об оценивании погрешности, в отечественной метрологической практике подразумевают оценивание ее характеристик [11]:
|
Погрешность |
|
Характеристика |
|
Алгоритм |
|
Оценка характеристики |
|
|
|
погрешности |
|
оценивания |
|
погрешности |
2. В Руководстве для выражения точности измерений вводят понятие неопределенности измерений. Неопределенность измерений понимают как неполное знание значения измеряемой величины и для количественного выражения этой неполноты вводят распределение вероятностей возможных (обоснованно приписанных) значений измеряемой величины. Таким образом, параметр этого распределения (также называемый - неопределенность) количественно характеризует точность результата измерений.
З. Сходными для обоих подходов являются последовательности действий при оценивании характеристик погрешности и вычислении неопределенности измерений:
- анализ уравнения измерений;
- выявление всех источников погрешности (неопределенности) измерений и их количественное оценивание;
- введение поправок на систематические погрешности (эффекты), которые можно исключить.
4. Методы вычисления неопределенности, также как и методы оценивания характеристик погрешности, заимствованы из математической статистики, однако при этом используются различные интерпретации закона распределения вероятностей случайной величины. Кроме изложенных в Руководстве и отечественных НД на практике используют и другие методы вычисления неопределенности и оценивания характеристик погрешности.
Возможны различия между оценками характеристик погрешности (в соответствии с отечественными НД) и неопределенностями (в соответствии с Руководством).
Различие
двух подходов проявляется также в
практике неопределенности и характеристик
погрешности, основанной на разных
интерпретациях вероятности: частотной
и субъективной. В частности, доверительные
границы погрешности (отложенные от
результата измерений) накрывают истинное
значение измеряемой величины с заданной
доверительной вероятностью (частотная
интерпретация вероятности), В то же
время аналогичный интервал (у- ,у
+U
р)
трактуется в
Руководстве
как интервал, содержащий заданную долю
распределения значений, которые могли
бы быть обоснованно приписаны измеряемой
величине (субъективная интерпретация
вероятности).
,у
+U
р)
трактуется в
Руководстве
как интервал, содержащий заданную долю
распределения значений, которые могли
бы быть обоснованно приписаны измеряемой
величине (субъективная интерпретация
вероятности).
5. В общем случае не существует однозначного соответствия между случайными погрешностями и неопределенностями, вычисленными по типу А (а также неисключенными систематическими погрешностями и неопределенностями, вычисленными по типу В). Деление на систематические и случайные погрешности обусловлено природой их возникновения и проявления в ходе измерительного эксперимента, а деление на неопределенности, вычисляемые по типу А и по типу В - методами их расчета.
Вместе с тем можно (с осторожностью) отметить, что ряд используемых в действующей нормативно-технической документации характеристик погрешности по существу не отличаются от показателей неопределенности — это те же средние квадратические (стандартные) отклонения и доверительные границы (интервалы), но описанные другими словами. Имеющиеся различия связаны с терминологией, некоторыми особенностями расчета и т. д.
6. Некоторое методологическое различие имеется в подходе к определению коэффициента охвата, соответствующего коэффициенту k (k - коэффициент зависимости отдельных НСП от выбранной доверительной вероятности РД при их равномерном распределении), который традиционно используют в отечественной нормативной документации для определения общей границы неисключенной систематической погрешности, незначительно сказывается на результатах оценивания характеристик погрешности (неопределенности) измерения в практических задачах.
Переход к неопределенности вносит единообразие и четкий порядок в проблему описания и представления качества измерений.
Результаты сравнительного анализа процедур оценивания характеристик погрешности и вычисления неопределенности измерений приведены в табл.1 и 2.
Не предполагается, что Руководство однозначно и быстро заменит действующие национальные стандарты. Однако нормативные документы практически не используют понятия «неопределенность измерения» и ориентированы на устоявшийся подход, основанный на понятиях «погрешность» и «характеристики погрешности». Отметим стандарты на общие требования к средствам измерений, на методы поверки, методики выполнения измерений,
В последнее время усилился процесс интеграции Российской Федерации в международное сообщество, который требует гармонизации отечественных стандартов, в том числе в области метрологии и сертификации продукции, для устранения барьеров в торговом, промышленном и научном обмене и сотрудничестве. Поэтому при разработке новых редакций нормативных документов Российской Федерации рекомендации Руководства должны быть учтены. Изменения будут вводиться постепенно и в течение продолжительного времени. Возможно параллельное существование и использование действующих нормативных документов Российской Федерации и Руководства.
Областями, в которых использование Руководства обязательно, в настоящий момент являются измерения, проводимые в процессе международных сличений исходных национальных эталонов, и оказание калибровочных услуг зарубежным организациям. При этом ряд рекомендаций по выражению неопределенности в измерении уже вошли в некоторые нормативные документы метрологических органов Российской Федерации (например, ГОСТ 8.563-96 и ГОСТ Р 8.000-2000 [1]). Кстати, пока концепция оценки неопределенности результата измерений не распространяется на вопросы, связанные с нормированием метрологических характеристик средств измерений.
Табл.1 Процедура оценивания характеристик погрешности результата измерений
|
Погрешность |
| |||
|
Модель погрешности |
P(x;E, | |||
|
Характеристики погрешностей |
S –СКО |
Систематической погрешности |
| |
|
Исходные данные для оценивания характеристик погрешности |
| |||
|
Методы оценивания характеристик: 1.случайных погрешностей
2.Неисключенных систематических погрешностей
3.Суммарной погрешности
|
где
k= 1, при р = 0,99; | |||
|
Форма представления характеристик погрешности |
|
| ||
|
Интерпретация полученных результатов |
Интервал ( | |||
Табл.2. Процедура вычисления неопределенности измерений
|
Модель неопределенности (представление знания о значении измеряемой величины |
| ||
|
Неопределенность (количественная мера) |
Стандартная U |
Cуммарная
|
Расширенная
|
|
Исходные данные для вычисления неопределенности |
| ||
|
Методы вычисления неопределенности: |
| ||
|
| ||
|
| ||
|
| ||
|
Представление неопределенности |
| ||
|
Интерпретация полученных результатов |
Интервал (y- | ||
И в заключение попытаемся сформулировать основной вывод из данного материала[12]: специалист, владеющий приемами оценки погрешностей, достаточно легко может научиться характеризовать качество полученных результатов в терминах и показателях неопределенности, поскольку исходные положения, методы расчетов и правила оценки погрешности и неопределенности сравнительно близки. Существенно отличаются только правила сложения составляющих (в сторону упрощения — закон распространения неопределенностей) и (частично) форма представления результатов.
Дискуссия по поводу концепции неопределенности и ее применения продолжается до сих пор как внутри страны, так и за рубежом. Однако следует напомнить известный в метрологии комментарий [12 ]: «Так же, как система единиц СИ, будучи системой практически универсального использования, привнесла согласованность во все научные и технические измерения, всемирное единство в оценке и выражении неопределенности измерения обеспечило бы должное понимание и правильное использование широкого спектра результатов измерений в науке, технике, промышленности и регулирующих актах».




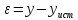 ,
y =
,
y =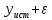
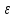 -
случайная величина с плотностью
распределения вероятностей
-
случайная величина с плотностью
распределения вероятностей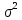 ,…),E– математическое
ожидание,
,…),E– математическое
ожидание,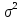 -
дисперсия
-
дисперсия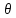 -
граница неисключенной
-
граница неисключенной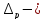 доверительные
границы
доверительные
границы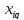 ;q= 1,…,
;q= 1,…, ;I= 1,…,m.
;I= 1,…,m.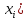 ,
,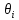 ,
структурная модель погрешности.
,
структурная модель погрешности.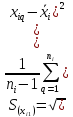 ;
;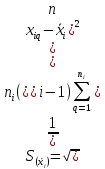 ;
;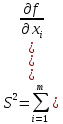
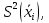
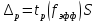 .
.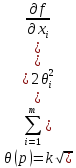 .
.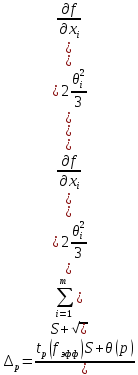
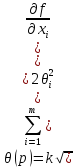 ,
k= 1,1 при р = 0,95;
,
k= 1,1 при р = 0,95; S =
S =
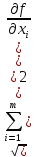
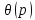 ,
S,
n
,
S,
n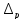
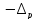 ,
,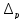 )
с вероятностьюр содержит погрешность
измерений, что равносильно тому, что
интервал (y
)
с вероятностьюр содержит погрешность
измерений, что равносильно тому, что
интервал (y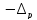 ,y
,y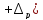 ,
с вероятностьюр содержит истинное
значение измеряемой величины.
,
с вероятностьюр содержит истинное
значение измеряемой величины.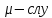 чайная
величина с плотностью распределения
вероятностей р(x;y,
чайная
величина с плотностью распределения
вероятностей р(x;y,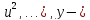 математическое
ожидание,
математическое
ожидание,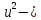 дисперсия.
дисперсия.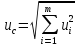
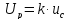
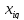 ;q= 1,…,
;q= 1,…,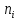 ;I= 1,…,m.
;I= 1,…,m.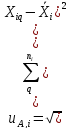 ,
,
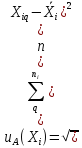 ,
, (
(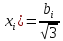
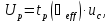
 ,
,
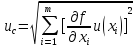 .
.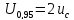 ,
,
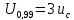 –для нормального закона;
–для нормального закона;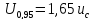 ,
,
 равномерного
зкона.
равномерного
зкона.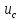 ,
,
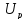 ,k,
,k,
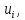
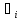
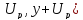 содержит большую долю (р) распределения
значений, которые могли бы быть
обосновано приписаны измеряемой
величине.
содержит большую долю (р) распределения
значений, которые могли бы быть
обосновано приписаны измеряемой
величине.