Основные понятия

В теории принятия решений используются процедуры выбора наилучшей из нескольких возможных альтернатив. Процесс принятия решения может принадлежать к одному из трех возможных условий:

1. принятие решений в условиях определенности, когда данные известны точно;

2. принятие решений в условиях риска, когда данные можно описать с помощью вероятностных распределений;

3. принятие решений в условиях неопределенности, когда данным нельзя приписать относительные веса (весовые коэффициенты), которые представляли бы степень их значимости в процессе принятия решений.

По существу, в условиях определенности, данные надежно определены, в условиях неопределенности они не определены. Принятие решений в условиях риска, следовательно, представляет “промежуточный” случай.

Часть 1. Принятие решения в условиях определенности Метод анализа иерархий

1.1 Постановка задачи

1. Сформулировать задачу принятия решения в условиях определенности с 2 иерархическими уровнями.

2. На основе искомых данных задачи выбрать оптимальную альтернативу.

1.2 Описание алгоритма решения задачи

Модели линейного, динамического, сепарабельного и т.д. программирования являются примером принятия решений в условиях определенности. Эти модели применимы лишь в тех случаях, когда альтернативные решения можно связать между собой точными линейными функциями. Но существует и иной подход к принятию решений в условиях определенности, когда определяются некоторые количественные показатели, обеспечивающие числовую шкалу предпочтений для возможных альтернативных решений. Этот подход известен как метод анализа иерархий.

Этапы решения задачи:

1. Получить матрицы парных сравнений критериев и матрицы парных сравнений альтернатив в рамках каждого критерия от всех экспертов.

Если имеется n критериев на заданном уровне иерархии, то создается матрица А размерности , именуемую матрицей парных сравнений, которая отражает суждение лица, принимающего решение, относительно важности разных критериев. Парное сравнение выполняется таким образом, что критерий в строкеi (i=1, 2, …, n) оценивается относительно каждого из критериев, представленных n столбцами. Обозначим через a_ij элемент матрицы А, находящийся на пересечении i –строки и j – столбца. В соответствии с методом анализа иерархий для описания упомянутых оценок используются целые числа от 1 до 9. При этом a_ij=1 означает, что i –й и j – й критерий одинаково важны, a_ij=5 отражает мнение, что i –й критерий значительно важнее, чем j – й, а a_ij=9 указывает, что i –й критерий чрезвычайно важнее и j – го Другие промежуточные значения между 1 и 9 интерпретируются аналогично. На матрицу парных сравнений накладываются следующие ограничения:

1. если a_ij=k, то a_ji=1/k.

2. все диагональные элементы a_ij матрицы А должны быть равны 1, так как они выражают оценки критериев относительно самих себя.

1. Определить относительные веса w критериев и альтернатив путем нормализации матрицы А ( деление элементов каждого столбца на сумму элементов этого же столбца). Искомые относительные веса w вычисляются теперь в виде средних значений элементов соответствующих строк нормализованной матрицы А.

2. Определить согласованность матрицы A. Согласованность означает, что решение будет согласовано с определениями парных сравнений критериев или альтернатив. С математической точки зрения согласованность матрицы A означает, что 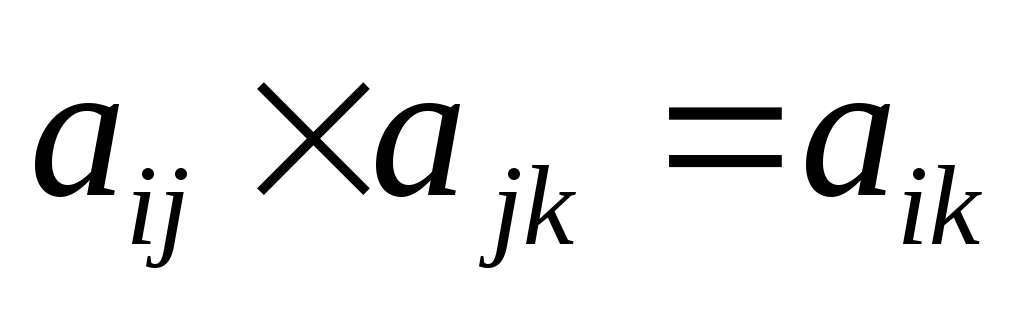для всех i, j и k. Свойство согласованности требует линейной зависимости столбцов (и строк) матрицы А. В частности, столбцы матрицы сравнения размером являются зависимыми, и, следовательно, такая матрица всегда является согласованной. Не все матрицы сравнений являются согласованными, так как строятся на основе человеческих суждений. При этом необходимо определить: является ли уровень несогласованности приемлемым. Чтобы выяснить, является ли уровень согласованности допустимым, необходимо определить соответствующую количественную меру для матрицы сравненийА. Идеально согласованная матрица А порождает нормализованную матрицу N, в которой все столбцы одинаковы.

.

Матрица сравнений А может быть получена из матрицы N путем деления элементов i-го столбца на w_i ( это процесс, обратный нахождению матрицы N из А).

.

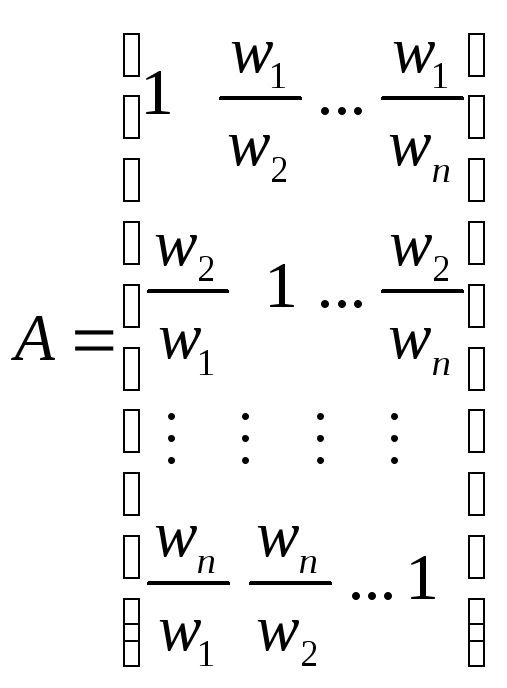Используя приведенное определение матрицы А, имеем

.

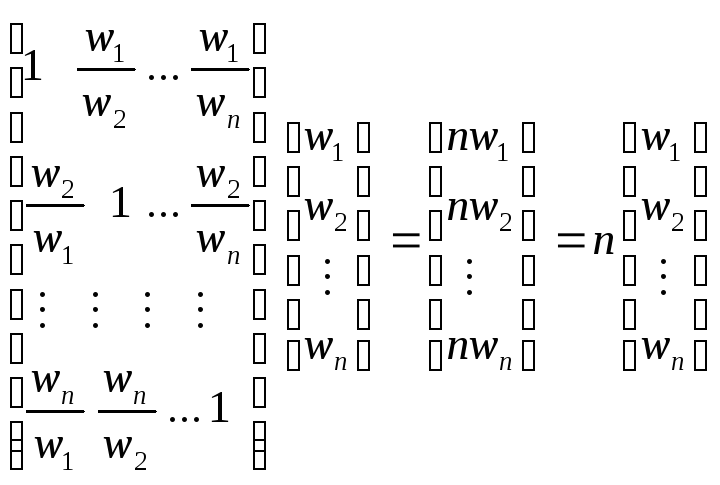В компактной форме условие согласованности матрицы А формулируется следующим образом. Матрица А будет согласованной тогда и только тогда, когда

Aw = nw,

где w – вектор столбец относительных весов w_i, i = 1, 2, …, n.

Когда матрица А не является согласованной, относительный вес w_i аппроксимируется средним значением n элементов i-й строки нормализованной матрицы N. Обозначив через вычисленную оценку (среднее значение в строке), условие согласованности матрицы можно записать

A = n_max ,

где . В случаеn_maх= n матрица сравнения А является идеально согласованной.

Уровень несогласованности матрицы A вычисляется из выражения

,

где

- коэффициент согласованности матрицы А,

- стохастический коэффициент согласованности матрицы А.

Стохастический коэффициент согласованности RI определяется эмпирическим путем как среднее значение коэффициента CI для большой выборки генерированных случайным образом матриц сравнения А.

Если , уровень несогласованности является приемлемым. В противном случае уровень несогласованности матрицы сравненияА является высоким и лицу, принимающему решение, рекомендуется проверить элементы парного сравнения a_ij матрицы A в целях получения более согласованной матрицы.

Значение n_max вычисляется на основе матричного уравнения , при этом нетрудно заметить, чтоi-е уравнение этой системы имеет вид:

, i = 1, 2, …, n.

Поскольку , сумма элементов в столбце расчетной матрицы может быть записана в следующем виде

.

Таким образом величину n_max можно определить путем вычисления вектор-столбца с последующим суммированием его элементов.

4. На основе полученных весовых коэффициентов находится комбинированный вес для каждой альтернативы.

5. Альтернатива, комбинированный весовой коэффициент которой является наибольшим, представляет собой оптимальное решение.