Статистика (1 сем

Относительная величина интенсивности – это отношение абсолютной величины изучаемого явления к абсолютной величине характеризующей объем среды в которой происходит развитие или распространение явления.

К этим величинам относятся: показатели потребления продуктов питания на душу населения, различные соц. показатели, экономические показатели, фондоотдача, фондоемкость и т.д.

IV.3Средняя величина – это обобщающий показатель характеризующий типичный размер определенного признака у единиц качественно-однородной совокупности.

Статистические средние рассчитываются на основе массовых данных правильно организованного массового наблюдения; считается что стат. средняя будет объективна, если она рассчитывается по данным качественно-однородной совокупности. Если совокупность не однородна, то необходимо ее расчленить на группы из которых затем исчислить средние – в этом заключается связь метода средних и группировок.

Средняя величина – величина абстрактная, потому что характеризует значения абстрактной единицы, которой может и не быть в совокупности; величина именованная, имеющая размерность признака.

IV.4Все средние величины выходят из одной степенной средней: , где

х – варианты осредняемого признака,

n – число вариантов,

m – показатель степени средней.

При: 1) m=1 - средняя арифметическая

2) m=0 - средняя геометрическая

3) m= -1 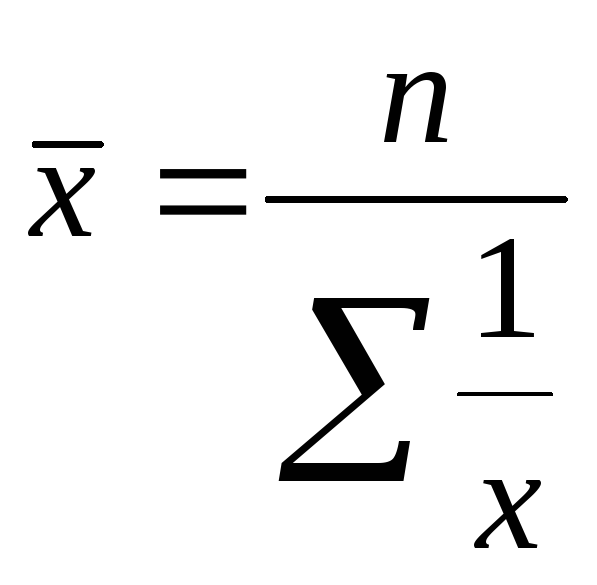- средняя гармоническая

4) m=2 - средняя квадратическая

5) m=3 - средняя кубическая

Все виды средних могут быть исчислены по индивидуальным значениям осредняемого признака – называется простая или не взвешенная; по сгруппированным с указанием весов – взвешенная средняя. Разные виды средних при одних и тех же исходных данных имеют различные значения: чем выше показатель m, тем больше величина соответствующей средней. _гарм <_геом < _ариф < _{квадрат}

Правило Мажорантности – это свойство средних возрастать с повышением показателей степени определяющей функции.

Наиболее часто применяются средняя арифметическая (простая) (взвешенная), и средняя гармоническая 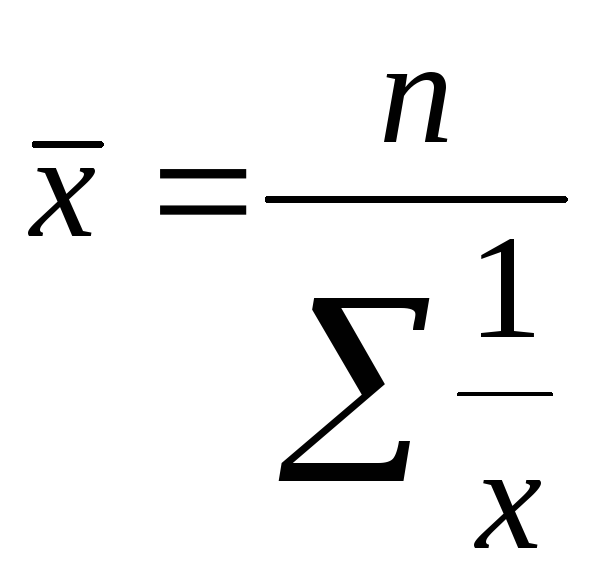(простая) 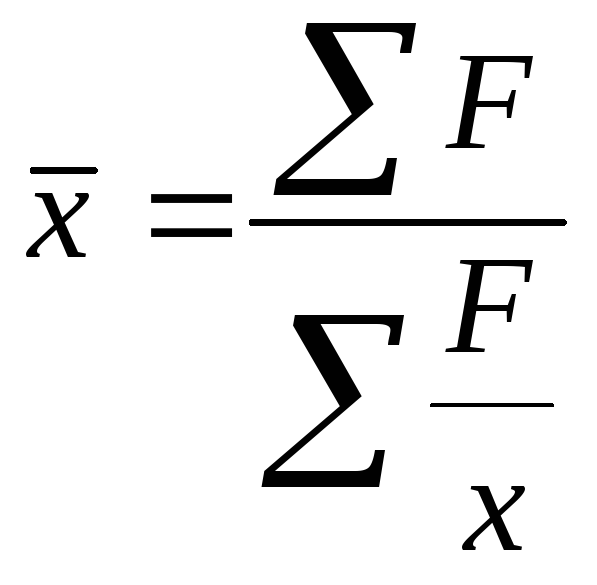(взвешенная).

IV.5Средняя арифметическая обладает рядом математических свойств, которые имеют важное значение для упрощения расчетов средней ()

- если все значения признака уменьшить (увеличить) на одно и тоже произвольное число, то новая средняя арифметическая будет меньше (больше) на то самое число ()

- если все значения признака разделить (умножить), то новая средняя уменьшится (увеличится) во столько же раз ( )

- средняя арифметическая постоянной величины равна этой постоянной (если х=с то )

- если все частоты разделить или умножить на какое-либо произвольное число, то средняя от этого не измениться ()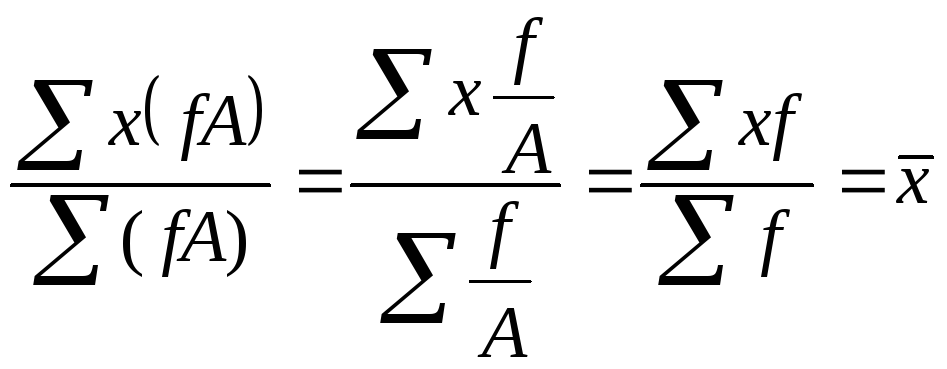

- произведение средней на сумму частот всегда равно сумме произведений вариант на частоты ()

- сумма положительных и отрицательных отклонений индивидуальных значений признака от средней равна нулю ().

IV.6Свойства средней арифметической применяем для упрощения расчетов.

СПОСОБ ОТСЧЕТА ОТ УСЛОВНОГО НУЛЯ или СПОСОБ МОМЕНТОВ:

1. из всех значений признака вычесть произвольную постоянную величину – лучше значение серединной варианты или варианты имеющей наибольшую частоту.

2. разность разделить на постоянное число – лучше величину интервала

3. исчисленную среднюю в обратной последовательности умножить на постоянное число и прибавить произвольную постоянную величину

, где m₁ – момент первого порядка,

IV.7.Мода и медиана для характеристики структуры совокупности.

Мода (Мо) - это наиболее часто встречающаяся величина признака в совокупности; она величина конкретная, имеющая свое определенное место; находится в дискретном и интервальном ряду. В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, который имеет наибольшую частоту, в пределах этого интервала надо найти то значение признака, которое является модой, конкретное значение моды определяется формулой:

Мо = , где Х_Мо – нижняя граница модального интервала,

h – величина интервала, f_Mo – частота модального интервала, f_-1 – частота предмодального интервала, f₊₁ –частота послемодального интервала.

Медиана (Ме) – это величина которая делит численность упорядоченного вариационного ряда на 2 равные части: одна часть имеет значения варьирующего признака меньше, чем средний вариант, а другая – большая. Она рассчитывается для дискретного и интервального ряда. ДЛЯ ДИСКРЕТНОГО:1)для ранжированного ряда с нечетным числом членов медианой является вариант расположенный в центре ряда. 2) для ранжированного ряда с четным числом членов медианой будет среднеарифметическая из 2-х смежных вариант ближе к середине. В ИНТЕРВАЛЬНОМ РЯДУ порядок нахождения медианы следующий:

1) расположить индивидуальные значения признака по ранжиру;

2) определить для данного ряда накопленные частоты;

3) по данным о накопленных частотах найти медианный интервал, т.к. медиана делит ряд пополам, то она там где накопленная частота составляет половину (это ее порядковый номер). Ме = 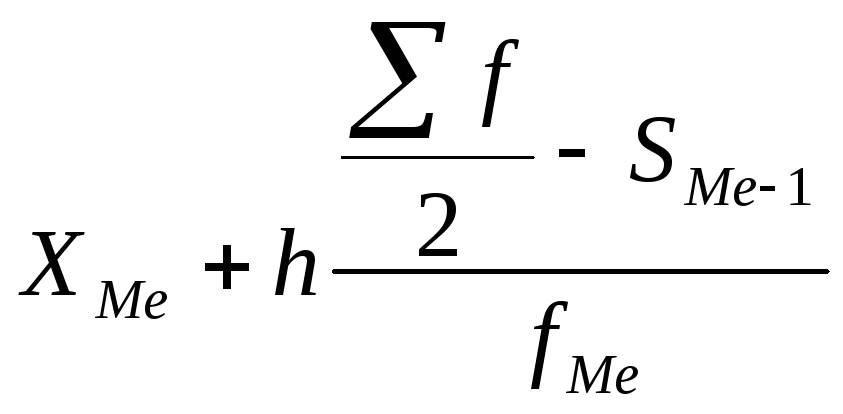, где Х_Ме – нижняя граница медианного интервала, - порядковый номер медианы, S_Ме-1 – сумму накопленных частот предшествующих медианному интервалу (кумулятивные частоты), f_Me – частота медианного интервала.

IV.8 Показатели вариации.

Вариация признака – это различие индивидуальных значений признака внутри изучаемой совокупности. Два ряда распределения могут иметь одинаковую среднюю величину, но в первом ряду отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются, а в другом отдельные значения далеко отстают от средней – значит она плохо представляет всю совокупность и является ненадежной характеристикой. Показатели вариации служат характеристикой типичности надежности самой средней. Чем меньше вариация, тем средняя более показательна, типична и наоборот – чем больше индивидуальные значения признака колеблются вокруг средней тем она менее типична. Показатели вариации служат для характеристики равномерности работы предприятия. Степень близости данных отдельных единиц к средней измеряется рядом абсолютных средних и относительных показателей:

I) абсолютные и средние показатели вариации:

1. размах вариации,

2. средние линейные отклонения,

3. дисперсии,

4. средние квадратичные отклонения.

II) относительные показатели вариации – коэффициент вариации.

Размах вариации представляет собой разность между наибольшим и наименьшим значением признака. R= X_max-X_min размах вариации зависит только от 2-х крайних значений признака, поэтому он недостаточно правильно отражает колеблемость.

Среднее линейное отклонение представляет собой среднюю из абсолютных величин отклонений всех значений от их среднеарифметической без учета знака отклонений: (простое), (взвешенное).

Дисперсия – это средний квадрат отклонений каждой величины от средней арифметической: (простая), (взвешенная).

Среднеквадратичное отклонение – это корень квадратный из дисперсии: (простое), (взвешенное).

Дисперсия и среднеквадратичное отклонение является общепринятыми мерами вариации признака; среднеквадратичное отклонение является мерилом надежности средней, чем меньше среднеквадратичное отклонение, тем лучше средняя арифметическая отражает собой всю совокупность.

Коэффициент вариации – это отношение среднеквадратичного отклонения к средней величине:. По его значению можно охарактеризовать однородность совокупности: если он не более 33,3%, то совокупность однородна и средняя типична.

Математические свойства дисперсии:

1. если из всех значений вариант вычесть постоянное число, то дисперсия от этого не изменится

2. если все значения вариант разделить на какое-то постоянное число а то дисперсия уменьшится от этого в а² раз

3. дисперсия от средней всегда меньше дисперсии исчисленных от любых других величин и в этом случае при А=0 формула дисперсии имеет вид:, где 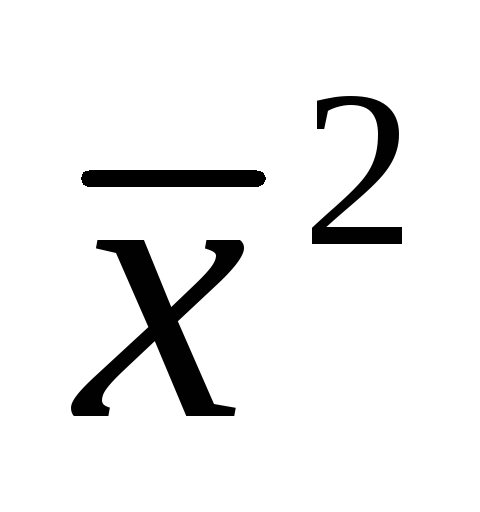= 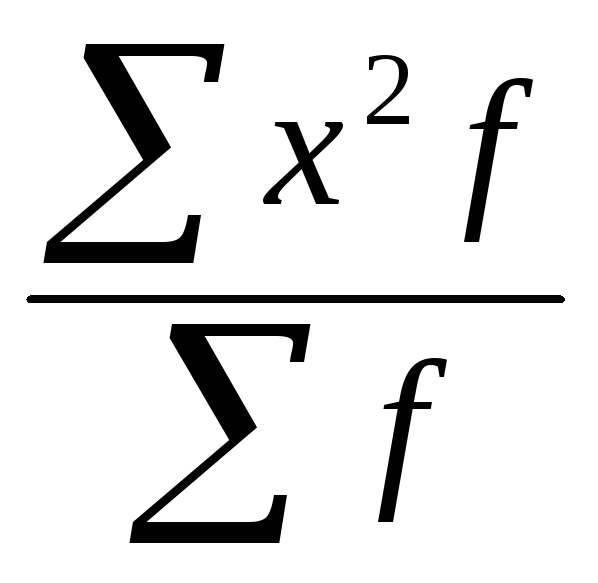- средний квадрат значений признака;

= - среняя арифметическая взвешенная.

Способ отсчета от условного нуля или способ моментов применим при условии равных интервалов, используя 2-е свойство дисперсии, разделив все варианты на величину интервала получим формулу , где m₁ - первый начальный момент; 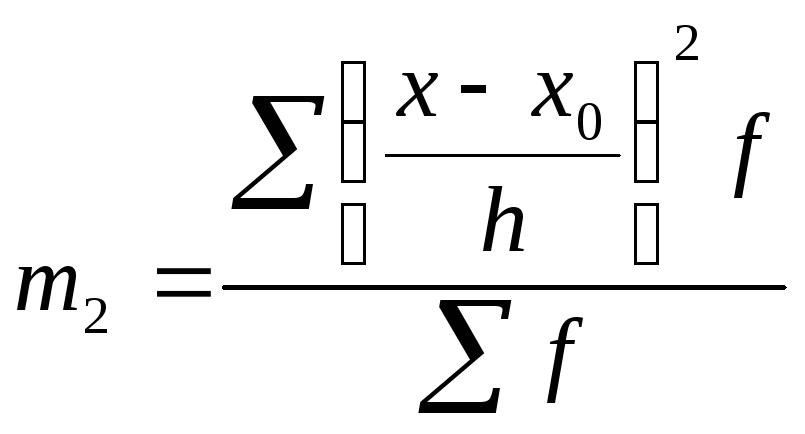- второй начальный момент. Формула дисперсии методом отсчета от условного нуля: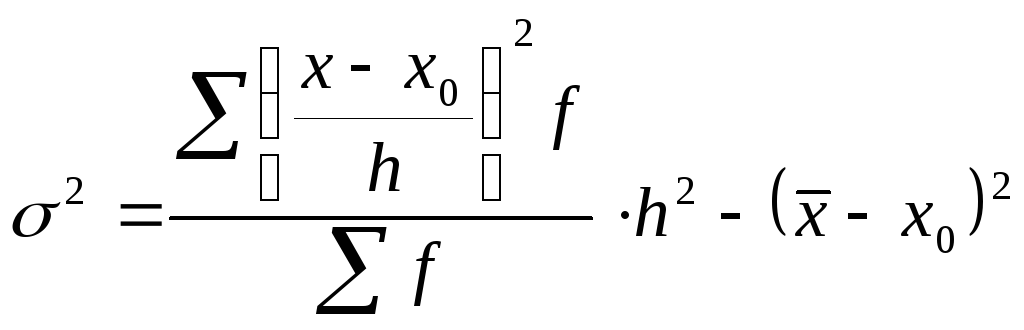

V .1

Индекс в статистике – обобщающий относительный показатель, характеризующий изменения в пространстве и во времени сложной совокупности, состоящей из отдельных элементов, непосредственно не поддающихся суммированию.

Индексы классифицируются по ряду признаков:

1. в зависимости от степени обхвата единиц изучаемой совокупности:

-индивидуальные (элементарные) – индексы, характеризующие изменение отдельных элементов сложной совокупности

-групповые индексы – те, которые охватывают не все элементы сложной совокупности, а только какую-то ее часть

-общие – индексы, характеризующие изменение сложной совокупности в целом

2. в зависимость от объектов исследования индексы делятся на:

-индексы объемных (кол-ных) показателей; к ним относятся индексы физического объема продукции, товарооборота, национального дохода и т.д., во всех этих индексах кол-во оценивается в одинаковых неизменных ценах

-индексы кач-ных показателей; к ним относятся индексы цен, себестоимости, производительности труда, трудоемкости и т.д., все эти индексы рассчитываются, исходя из неизменных количеств продукции

3. в зависимости от методологии расчета общие, групповые индексы могут быть:

-агрегатные – основная форма индекса

-средние из индивидуальных индексов – это производные, которые получаются в результате преобразования агрегатного индекса

Свойства общих, групповых индексов.

1. Синтетические – то, что посредством индексного метода производится соединение (агрегирование) в целое разнородных единиц стат. совокупности.

2. Аналитические свойства – это то, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.

Основным элементом индексного отношения является индексируемая величина – значение признака стат. совокупности, изменение которого является объектом изучения.

Стат. символика:

q - физический объем продукции

p – цена единицы продукции

z – себестоимость единицы продукции

t – трудоемкость, или затраты времени на единицу продукции

w – выработка

T – трудозатраты на производство всей продукции

рq – выручка, или стоимость всей продукции

zq – затраты на производство всей продукции

i – индивидуальный индекс

, А – один вид продукции, 1 – текущий период, 0 – базисный период

I – групповой (общий) индекс

V.2

Основной формой общих индексов являются агрегатные индексы; агрегатным индекс называется потому, что его числитель и знаменатель представляют собой агрегат, т.е. набор разнородных элементов. Агрегатный индекс рассчитывается как отношение суммы индексируемых величин сравниваемых периодов на соизмерители (веса); при этом в числителе и знаменателе общего индекса изменяется только индексируемая величина, а соизмерители являются постоянными величинами и фиксируются на одном уровне, это необходимо для того, чтобы на величине индекса сказывалось лишь влияние фактора, который определяет изменение индексируемой величины.

В статистике принято индексы кол-ных или объемных показателей строить с весами базисного периода, а индексы кач-ных показателей – с весами отчетного периода.

Для определения общего изменения цен и кол-ва реализованных товаров вычисляют соответствующие общие индексы:

1. общий индекс цен в агрегатной форме

При сравнении числителя и знаменателя формулы в разности определяется показатель абсолютного прироста товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным.

2. индекс физического объема в агрегатной форме

Прирост суммы товарооборота за счет изменения физического объема в текущем периоде по сравнению с базисным:

3. индекс товарооборота в агрегатной форме

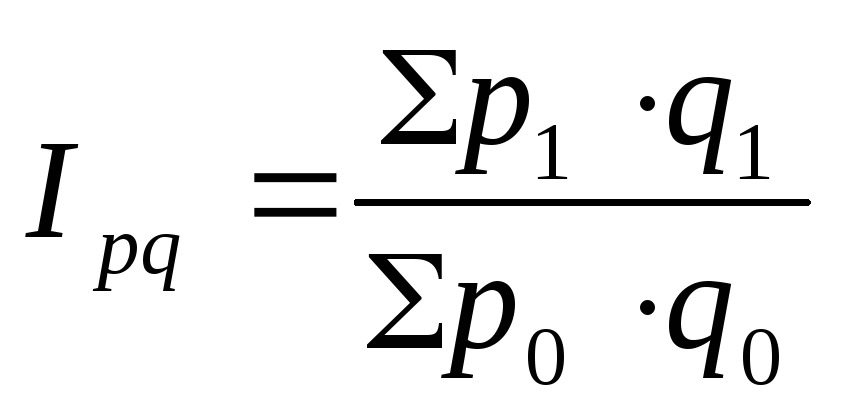
Общий индекс одновременно является и индексом средней из индивидуальных индексов, он является средней взвешенной величиной, необходимо правильно выбрать форму средней и систему весов для индивидуальных индексов.

V.3

Основное правило построения средних индексов: средний из индивидуальных должен быть тождественен исходному агрегатному индексу – это преобразованная форма агрегатного индекса. Средние могут быть 2-х видов: ср. арифметические и ср. гармонические. Чтобы ср. арифметический индекс был тождественен агрегатному, весами индивидуальных индексов в нем должны быть взяты слагаемые знаменателя исходного агрегатного индекса; чтобы ср. гармонический индекс был тождественен агрегатному, весами должны быть взяты слагаемые числителя агрегатного индекса.

Значимость преобразованных индексов состоит в том, что в кач-ве весов осредняемых индексов выступают реальные экономические категории:

1) и - фактический товарооборот текущего и базисного периодов;

2) и - фактические затраты денежных средств на производство продукции в текущем и базисном периодах

3) и - фактические затраты рабочего времени на производство продукции в текущем и базисном периодах

Наименование индекса	Индивидуальный индекс	Агрегатная форма индекса	Ср. арифметический индекс	Ср. гармонический индекс
Индекс физического объема
Индекс цены

V.4

В ряде случаев требуется сравнить данные не за 2 периода, а за 3 и более периодов. В таких случаях необходимо выбрать базу сравнения, и в зависимости от базы сравнения различают индексы:

1. базисные – имеют один и тот же период времени, взятый за базу сравнения;

2. цепной – за базу сравнения беру период, предшествующий вычислению индекса.

Цепные и базисные индексы могут быть с переменными или постоянными весами. Индексы с постоянными весами вычисляются по весам одного какого-то периода, а индексы с переменными весами вычисляются по весам индексируемых периодов.

Цепные и базисные индексы с постоянными весами находятся в след. зависимости:

1. произведение цепных индексов дает базисный индекс последнего периода

2. деление последующего базисного индекса на предыдущий базисный индекс дает цепной индекс последующего периода

Построим 4 ряда индексов по 3-м периодам.

1. базисные индексы цен с постоянными весами

;

2. цепные индексы цен с постоянными весами

;

3. базисные индексы цен с переменными весами

;

4. цепные индексы цен с переменными весами

;

V.5

Индексный метод широко применяется для анализа роли отдельных факторов в динамике какого-либо сложного явления, изменение которого обусловлено действием нескольких факторов, выступающих как множители совокупного результата. Так динамика товарооборота обусловлена совместным изменением кол-ва проданных товаров и цен на них.

Чтобы образовать систему индексов, необходимо веса в индексах брать на разных уровнях. Индексной системой часто пользуются для расчета третьего показателя, если известны 2 других, входящих в систему.

V.6

Характеризуя динамику какого-либо явления, мы пользуемся, наряду с объемными показателями, также и средними кач-ными показателями; для их характеристики применяются индексы переменного, фиксированного (постоянного) состава и структурных сдвигов. Изменение средней величины любого показателя зависит от изменения значения каждой отдельной единицы изучаемого явления и изменения структуры явления.

1. Индекс переменного состава – характеризует совместное влияние 2-х факторов, в нем меняются обе величины

, где х – осредняемый признак (средняя величина), d – доля изучаемого явления

2. Индекс постоянного (фиксированного) состава характеризует влияние только индексируемой величины, именно она и меняется в индексе

3. Индекс структурных сдвигов характеризует изменение влияния структуры на среднюю величину

VI.1. Изменение общественного процесса или явлений во времени называется динамикой.

Ряды динамики- ряды, последовательно расположенных в хронологическом порядке показателей, характеризующих динамику общественного явления, они характеризуются 2-мя показателями;

1) показатель времени- t

2) уровень ряда-y

В зависимости от вида приводимых обобщающих показателей ряды динамики бывают: абсолютных, относительных и средних величин. Исходные – это ряды абсолютных величин. Производные- ряды относительных и средних величин.

Ряды динамики абсолютных величин бывают:

1) моментные ряды- они характеризуют уровни развития общественного явления на определенные моменты времени;

2) интервальные ряды- они характеризуют уровни развития общественного явления за определенные периоды времени.

моментные ряды- период между датами, на которые приводятся данные, называются интервалом; величина интервала зависит от характера явлений; в этом ряду в каждом последующем уровне содержится полностью или частично предыдущий уровень, поэтому суммировать уровни моментного ряда нельзя, т.к. это приведет к повторному счету; важное значение имеет определение разности уровней ряда динамики, которые характеризуют увеличение или уменьшение изучаемого явления во времени.

Интервальный ряд- ряд, характеризующий размер явления за определенный период (год, месяц, сутки.,) – ряды ежесуточные, ежемесячные, ежеквартальные, годовые; интервалом ряда считается промежуток времени, за который обобщены приводимые сведения, т.е. величина интервала- это накопленный итог учета результатов деятельности; важное значение для этого ряда является его суммирование его уровней, т.к. сумма уровней характеризует уровень данного явления за более длительный период.

VI.2. Для того, чтобы правильно построить ряд динамики, необходимо прежде всего обеспечить сопоставимость его показателей.

Основные причины несопоставимости показателей ряда динамики:

1) изменение административно-территориальных границ;

2) изменение единиц измерения или единиц счета;

3) изменение методологии подсчета статистических данных

4) различия в степени охвата явления наблюдением;

5) различия в периодах времени в экономическом отношении или по продолжительности.

При построении динамики рядов необходимо ликвидировать несопоставимость данных для чего:

1) пересчитываются старые данные в новых террит.- админ. границах;

2) выбираются равные одноименные интервалы;

3) смыкаются показатели рядов динамики путем замены абсолютных уровней относительными;

4) данные пересчитываются в одних единицах измерения и по одной методике расчета

VI.3. Для анализа динамики общественных явлений рассчитываются следующие показатели:

1) абсолютные приросты

2) темпы роста

3) темпы прироста

4) абсолютный размер 1 % прироста

5) средние показатели

Исходные уровни ряда:

• начальный уровень ряда -у - показывает величину 1-ого члена ряда

• конечный уровень - у- показывает величину конечного уровня ряда

• промежуточный уровень - у- показывает величину любого уровня ряда

Абсолютный прирост (у) показывает насколько данный уровень ряда больше или меньше уровня, принятого за базу сравнения он выражается в единицах измерения уровней ряда; они рассчитываются за отдельные периоды времени: