Питання для перевірки:

1. Яка функція називається зростаючою ( спадною ) ?

2. Сформулюйте необхідну і достатню умови зростання ( спадання ) функції.

3. Що називають максимумом ( мінімумом ) функції?

4. Як називають мінімум і максимум функції в точці?

5. В чому полягає необхідна умова існування екстремуму?

6. Сформулюйте достатню умову існування екстремуму.

7. Як називаються точки, в яких похідна дорівнює нулю?

8. Як називаються точки, в яких похідна дорівнює нулю або не існує?

9. Пригадайте правило, за яким знаходяться інтервали монотонності і екстремуми функції.

10. Як досліджується функція на екстремум за допомогою другої похідної?

11. Як знайти найбільше і найменше значення функції на відрізку?

Вправи

1. Показати, що функція 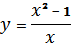зростає в будь-якому інтервалі, який не містить точкух=0.

2. Знайти інтервали монотонності функції .

Відповідь: в інтервалах (0;1) i (1;e) функція спадає, а в інтервалі (e;+∞)зростає.

3. Знайти інтервали зростання і спадання функції

Відповідь: функція монотонно зростає.

Вказівка. Скористались тим, що -1≤ sinx ≤ 1

4. Знайти екстремуми функції y = 2x³ – 3x²

Відповідь: y_max= 0 при х = 0, y_min = -1при х = 1.

5. Знайти екстремуми функції y = x – ln(1-x)

Відповідь: y_min = 0 при x = 0.

6. Знайти найбільше і найменше значення функції y = x⁵ – 5x⁴ + 5x³ + 1 на відрізку [-1;2].

Відповідь: 2 і -10.

7. Знайти найбільше і найменше значення функції на відрізку[0;4].

8. Показати, що функція зростає в інтервалі (0;1) і спадає в інтервалі ( 1;2).

9. Знайти екстремуми функції =x³ – 2ax² + a²x (a > 0) за допомогою другої похідної.

Відповідь: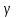_max = приx = ,y_min = 0 при x = a.

10. За допомогою другої похідної знайти екстремуми функції = x²e^-x.

Відповідь: 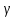_max = при х = 2, y_min = 0 при х = 0.

7. Опуклість і вoгнутість кривої. Точки перетину

Графік функції =f(x) називається опуклим (крива обернена опуклістю вгору) в інтервалі ( a;b ), якщо він розміщений нижче дотичної, проведеної в будь-якій точці цього інтервалу (рис. 14).

Графік функції називається вoгнутим (крива обернена опуклістю вниз) в інтервалі (а;b), якщо він розміщений вище дотичної, проведеної в будь-якій точці цього інтервалу ( рис. 15).

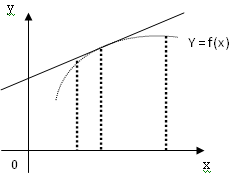
Рис.15

Рис.14

Якщо f ´(x) < 0 (f ´(x) > 0) в інтервалі (a;b), то графік функції опуклий

(вогнутий) в цьому інтервалі (достатня умова опуклості ( вoгнутості) графіка функції).

Точка ( x₀; f(x₀)) графіка функції, яка відділяє опуклу частину від вoгнутої, або навпаки, вoгнуту його частину від опуклої, називається точкою перегину ( рис.16).

Y = f(x)

y

0 x₀ x

Y = f(x)

y

0 x₀ x

Рис.16

Якщо (x₀;y₀) - точка перетину графіка функції y = ʄ(x), то друга похідна

ʄ ʹ(x₀)= 0 або ʄ ʹ(x₀) не існує (необхідна умова існування точки перегину).

Точки, в яких ʄ ʹ(x)=0 або ʄʹ(x) не існує, називають критичними точками другого роду.

Якщо при переході через критичну точку х₀ друга похідна змінює знак, то точка M(x₀;y₀) є точкою перегину кривої (достатня умова існування точки перегину).

Виходячи із цих умов, одержуємо правило знаходження інтервалів опуклості і вогнутості та точок перегину графіка функції ,яке пропонуємо застосовувати на практиці.

1. Знаходимо область визначення функції.

2. Знаходимо ʄ (х)

3. Знаходимо ʄ ʹ(х)

4. Знаходимо корені рівняння ʄ ʹ(х)=0 і точки, де ʄ ʹ(х) не існує( критичні точки другого роду.

5. Визначаємо знак другої похідної ʄ ʹ в кожному інтервалі , на які знайдені критичні точки, розбивають область визначення данної функції і тим самим знаходимо інтервали опуклості і вогнутості кривої.

Визначаємо, які із критичних точок є абсцисами точок перегину

Зауважимо, що в точці з абсцисою х₃ графік функції ʄ (x) має перегин, якщо в цій точці функція ʄ (x) визначена, або не має перегину, якщо функція

ʄ (x) в цій точці не визначена.

Обчислюємо значення функції ʄ(x) з знайдених точках, тобто знаходимо точки перегину графіка цієї функції.