
m0096 / ГИА-2013. Математика. Диагностическая работа 1. (вар. 1-8) 02.10.2012г. (с крит. оцен. С)
.pdf
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 1 |
1 |
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɡɚɞɚɧɢɣ ɫ ɪɚɡɜɺɪɧɭɬɵɦ ɨɬɜɟɬɨɦ |
|
Ɇɨɞɭɥɶ "Ⱥɥɝɟɛɪɚ"
21 |
|
ɍɩɪɨɫɬɢɬɟ ɜɵɪɚɠɟɧɢɟ |
|
|
10 |
2 |
10 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
10 |
2 |
10 |
2 |
|
|
( |
10 |
2)( |
10 |
2) |
|
|
|
10 |
4 |
|
6 |
|
1 |
|
|
|
1 |
. |
|
|||||||||
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
24 |
|
|
24 |
4 |
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ɉɬɜɟɬ |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
|
|
Ȼɚɥɥɵ |
||||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ ɜɟɪɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
1 |
|
||||||||||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
2 |
|
|||||||||||
Ʉɨɦɦɟɧɬ |
ɢɣ. Ɉɲɢɛɤɢ ɜ ɩɪɢɦɟɧɟɧɢɢ ɮɨɪɦɭɥ ɫɱɢɬɚɸɬɫɹ ɫɭɳɟɫɬɜɟɧɧɵɦɢ; |
ɩɪɢ ɢɯ |
||||||||||||||||||||||||||||||||||
ɧɚɥɢɱɢɢ ɪɟɲɟɧɢɟ ɧɟ ɡɚɫɱɢɬɵɜɚɟɬɫɹ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
22 |
|
Ɉɞɢɧ ɢɡ ɤɨɪɧɟɣ ɭɪɚɜɧɟɧɢɹ 3X2 |
5X |
2M |
|
0 ɪɚɜɟɧ 1. ɇɚɣɞɢɬɟ ɜɬɨɪɨɣ ɤɨɪɟɧɶ. |
|
|||||||||||||||||||||||||||||
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ɉɨɞɫɬɚɜɢɦ |
ɢɡɜɟɫɬɧɵɣ |
ɤɨɪɟɧɶ: |
ɜ ɭɪɚɜɧɟɧɢɟ |
3 |
|
5 |
|
2M |
0. |
ɉɨɥɭɱɢɦ |
ɭɪɚɜɧɟɧɢɟ |
|||||||||||||||||||||||||
ɨɬɧɨɫɢɬɟɥɶɧɨ M.Ɋɟɲɢɦ: |
ɟɝɨ 2M |
|
2; |
M 1. ɉɨɞɫɬɚɜɢɦ: |
M ɜ ɭɪɚɜɧɟɧɢɟ 3X2 |
5X |
2 0, |
|||||||||||||||||||||||||||||
ɨɬɤɭɞɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
5 r 25 4 3 2 |
|
5 r 1 |
, |
X |
1, X |
|
2 |
. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
1 |
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ɉɬɜɟɬ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
|
|
Ȼɚɥɥɵ |
||||||||||||||||||||||
ɵ ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ |
|
|
, |
|
|
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
2 |
|
||||||||||||||||||||||||||||||||||
ɨɩɢɫɤɚ ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
|
|
3 |
|
|||||||||
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 1 |
2 |
23ɇɚɣɞɢɬɟ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ ɜɵɪɚɠɟɧɢɹ ɢ ɡɧɚɱɟɧɢɹ X ɢ Y, ɩɪɢ ɤɨɬɨɪɵɯ ɨɧɨ ɞɨɫɬɢɝɚɟɬɫɹ 6X 5Y 7
 2X 3Y 1.
2X 3Y 1.
Ɋɟɲɟɧɢɟ
ɋɭɦɦɚ |
|
6X 5Y |
7 |
|
|
|
2X 3Y |
1 |
|
ɩɪɢɧɢɦɚɟɬ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ0, |
, ɪɚɜɧɨɟ |
ɬɨɥɶɤɨ ɜ |
|||||||||
|
|
|
|
||||||||||||||||||
ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɨɛɚ ɫɥɚɝɚɟɦɵɯ ɨɞɧɨɜɪɟɦɟɧɧɨ0. |
ɪɚɜɧɵ |
ɉɨɥɭɱɚɟɦ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
®X6 |
Y5 |
7 |
0, |
|
|
|
|
|
Ɋɟɲɢɦ: |
ɟɺ |
|
|
|
|
|
|
|
|
|
¯X2 |
Y3 |
1 |
0. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
X6 |
5Y 7 0, |
Y4 |
4 0, |
|
|
Y 1, |
Y 1, |
|
||||||||||
|
® |
|
|
|
|
|
® |
|
|
|
|
|
|
® |
|
|
® |
|
|
||
Ɉɬɜɟɬ |
|
|
¯X6 |
9Y 3 0; |
¯X6 |
9Y |
3 0; |
¯ |
6X |
12 0; |
¯ X |
2. |
|
||||||||
|
0; (–2;1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
Ȼɚɥɥɵ |
||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
4 |
|||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
3 |
||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺɞɨɜɟɞɟɧɨɭɱɺɬɨɦ ɪɟɲɟɧɢɟ |
|
|
|
|
ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
4 |
||
Ɇɨɞɭɥɶ "Ƚɟɨɦɟɬɪɢɹ"
24 ɇɚɣɞɢɬɟ ɜɟɥɢɱɢɧɭ ɭɝɥɚ AOE, ɟɫɥɢ– OE ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ AOC, OD – ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ COB.
Ɋɟɲɟɧɢɟ
COBAOE=2·25°=50°; =180°–50°=130°; =130°:2=65°.
Ɉɬɜɟɬ 65°.
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 1 |
|
|
|
|
|
3 |
|
||||
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
Ȼɚɥɥɵ |
|||||
Ɋɟɲɟɧɢɟ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
|
2 |
|
|||
Ⱦɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɟɬɨɦ |
1 |
|
|||||||||
ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
0 |
|
|||||||
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
2 |
|
|||
25 ȼ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɟ ABCD ɬɨɱɤɚ M — ɫɟɪɟɞɢɧɚ. |
ɫɬɨɪɨɧɵ, |
AB |
ɂɡɜɟɫɬɧɨ ɱɬɨ |
||||||||
|
MC |
MD. Ⱦɨɤɚɠɢɬɟ, ɱɬɨ ɞɚɧɧɵɣ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦ — ɩɪɹɦɨɭɝɨɥɶɧɢɤ. |
|
|
|||||||
ɉɭɫɬɶ |
ɬɨɱɤɚ Mɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ– ɫɟɪɟɞɢɧɚ ɫɬɨɪɨɧɵ AB |
|
|
ABCD – ɪɚɜɧɨɭɞɚɥɟɧɚ ɨɬ ɟɝɨ |
|
||||||
ɜɟɪɲɢɧ C ɢ D. Ɍɨɝɞɚ, ɬɪɟɭɝɨɥɶɧɢɤ CMD – ɪɚɜɧɨɛɟɞɪɟɧɧɵɣ, ɩɨɷɬɨɦɭ MCD |
MDC. |
||||||||||
ɉɨɫɤɨɥɶɤɭ |
ɩɪɹɦɚɹ |
CD ɩɚɪɚɥɥɟɥɶɧɚ |
, |
ɫɬɨɪɨɧɟ AB ɬɨ |
BMC |
MCD ɢ |
|||||
AMD |
MDC ɤɚɤ |
ɧɚɤɪɟɫɬ ɥɟɠɚɳɢɟ. |
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, +BMC |
+AMD ɩɨ |
ɩɟɪɜɨɦɭ |
||||||
ɩɪɢɡɧɚɤɭ( |
ɪɚɜɟɧɫɬɜɚ ɬɪɟɭɝɨɥɶɧɢɤɨɜ BMC |
AMD, AM |
BM, MC |
MD). |
|
|
|||||
Ɂɧɚɱɢɬ, CBM |
DAM. ɂɯ ɫɭɦɦɚ ,ɪɚɜɧɚ 180q |
ɬ ɤ. ɷɬɨ ɞɜɚ ɭɝɥɚ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ, |
|
ɩɪɢɥɟɠɚɳɢɟ ɤ |
ɨɞɧɨɣ ɫɬɨɪɨɧɟ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, |
CBM DAM |
90 . ɉɨ ɫɜɨɣɫɬɜɭ |
ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ ɭɝɥɵ BCD ɢ CDA ɬɚɤɠɟ ɩɪɹɦɵɟ. Ɂɧɚɱɢɬ, ABCD – ɩɪɹɦɨɭɝɨɥɶɧɢɤ. |
|||
Ʉɨɦɦɟɧɬ ɢɣ: |
Ɋɚɜɟɧɫɬɜɨ ɬɪɟɭɝɨɥɶɧɢɤɨɜ BMC ɢ AMD ɦɨɠɟɬ ɛɵɬɶ |
ɞɨɤɚɡɚɧɨ ɢɧɚɱɟ, |
|
ɧɚɩɪɢɦɟɪ, ɩɨ ɬɪɟɬɶɟɦɭ ɩɪɢɡɧɚɤɭ ɪɚɜɟɧɫɬɜɚ ɬɪɟɭɝɨɥɶɧɢɤɨɜ. |
|
||
Ⱦ ɭɝɨɟ ɜɨɡɦɨɠɧɨɟ ɞɨɤ ɡ ɬɟɥɶɫɬɜɨ:
ɉɭɫɬɶ– ɬɨɱɤɚ O |
ɫɟɪɟɞɢɧɚ CD. ɑɟɬɵɪɟɯɭɝɨɥɶɧɢɤ OMBC ɹɜɥɹɟɬɫɹ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɨɦ, |
||||
ɩɨɫɤɨɥɶɤɭ ɟɝɨ |
ɫɬɨɪɨɧɵ |
OC ɢ |
MB ɩɚɪɚɥɥɟɥɶɧɵ ɢ ɪɚɜɧɵ. Ɍɪɟɭɝɨɥɶɧɢɤ |
MCD – |
|
ɪɚɜɧɨɛɟɞɪɟɧɧɵɣ,– ɩɨɷɬɨɦɭ |
OM |
ɟɝɨ ɜɵɫɨɬɚ. Ɂɧɚɱɢɬ, OMBC– ɩɪɹɦɨɭɝɨɥɶɧɢɤ, |
|||
ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɭɝɨɥ– .CBM ɩɪɹɦɨɣ |
|
||||
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
||||
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ, |
ɜɟɪɧɨɟ ɜɫɟ ɲɚɝɢ ɨɛɨɫɧɨɜɚɧɵ |
3 |
|||
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ ɫɨɞɟɪɠɢɬ ɧɟɬɨɱɧɨɫɬɢ ɢɥɢ ɩɪɨɛɟɥɵ, ɧɚɩɪɢɦɟɪ, ɨɬɫɭɬɫɬɜɭɸɬ |
2 |
||||
ɫɫɵɥɤɢ ɧɚ ɫɜɨɣɫɬɜɚ ɩɚɪɚɥɥɟɥɶɧɵɯ ɩɪɹɦɵɯ ɢɥɢ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ |
|||||
|
|||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
0 |
||||
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
3 |
|
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 1 |
|
4 |
ɛɟɞɪɟɧɧɨɝɨ26 Ɉɫɧɨɜɚɧɢɟ AC |
ɬɪɟɭɝɨɥɶɧɢɤɚ ABC10. ɪɚɜɧɨ |
Ɉɤɪɭɠɧɨɫɬɶ |
ɪɚɞɢɭɫɚ 7, 5 ɫ ɰɟɧɬɪɨɦ ɜɧɟ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɤɚɫɚɟɬɫɹ ɩɪɨɞɨɥɠɟɧɢɹ ɛɨɤɨɜɵɯ ɫɬɨɪɨɧ ɬɪɟɭɝɨɥɶɧɢɤɚ ɢ ɤɚɫɚɟɬɫɹ ɨɫɧɨɜɚɧɢɹ AC ɜ ɟɝɨ ɫɟɪɟɞɢɧɟ. ɇɚɣɞɢɬɟ ɪɚɞɢɭɫ ɨɤɪɭɠɧɨɫɬɢ, ɜɩɢɫɚɧɧɨɣ ɜ ɬɪɟɭɝɨɥɶɧɢɤ ABC.
Ɋɟɲɟɧɢɟ
Ⱦɚɧɧɚɹ ɨɤɪɭɠɧɨɫɬɶ ɤɚɫɚɟɬɫɹ ɫɬɨɪɨɧɵ AC ɜ ɟɺ ɫɟɪɟɞɢɧɟ M ɢ ɩɪɨɞɨɥɠɟɧɢɣ ɫɬɨɪɨɧ BA BC ɬɪɟɭɝɨɥɶɧɢɤɚ ABC.
—ɉɭɫɬɶ O |
ɰɟɧɬɪ, |
ɷɬɨɣ ɨɤɪɭɠɧɨɫɬɢ ɚ Q—, |
ɰɟɧɬɪ ɨɤɪɭɠɧɨɫɬɢ ɜɩɢɫɚɧɧɨɣ ɜ |
ɬɪɟɭɝɨɥɶɧɢɤ ABC. ɍɝɨɥ OAQ – ɩɪɹɦɨɣ ɤɚɤ ɭɝɨɥ ɦɟɠɞɭ ɛɢɫɫɟɤɬɪɢɫɚɦɢ ɫɦɟɠɧɵɯ ɭɝɥɨɜ. Ɍɪɟɭɝɨɥɶɧɢɤ OAQ – ɩɪɹɦɨɭɝɨɥɶɧɵɣ, AM – ɟɝɨ ɜɵɫɨɬɚ. ɂɡ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ, ɧɚɯɨɞɢɦ
ɱɬɨ AM, |
2 MQ MO. ɋɥɟɞɨɜɚɬɟɥɶɧɨ QM |
|
AM2 |
|
10 |
. |
|
|||
|
OM |
3 |
|
|||||||
|
|
|
|
|
|
|
||||
Ɉɬɜɟɬ |
10 |
. |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
||||||
ɏɨɞ ɪɟɲɟɧɢɹ ɜɟɪɧɵɣ, ɜɫɟ ɟɝɨ ɲɚɝɢ ɜɵɩɨɥɧɟɧɵ ɩɪɚɜɢɥɶɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ |
4 |
|||||||||
ɨɬɜɟɬ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
ɏɨɞ ɪɟɲɟɧɢɹ, |
ɜɟɪɧɵɣ ɜɫɟ ɟɝɨ ɲɚɝɢ |
ɜɵɩɨɥɧɟɧɵ ɩɪɚɜɢɥɶɧɨ, ɧɨ ɞɚɧɵ |
3 |
|||||||
ɧɟɩɨɥɧɵɟ ɨɛɴɹɫɧɟɧɢɹ ɢɥɢ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɜɵɱɢɫɥɢɬɟɥɶɧɚɹ ɨɲɢɛɤɚ |
||||||||||
|
||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɜɵɲɟ ɤɪɢɬɟɪɢɹɦ |
0 |
|||||||||
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
4 |
|
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
1 |
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɡɚɞɚɧɢɣ ɫ ɪɚɡɜɺɪɧɭɬɵɦ ɨɬɜɟɬɨɦ |
|
Ɇɨɞɭɥɶ "Ⱥɥɝɟɛɪɚ"
21 |
|
ɍɩɪɨɫɬɢɬɟ ɜɵɪɚɠɟɧɢɟ |
|
|
|
|
54 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
15 |
3 |
|
15 |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
54 |
|
|
|
|
|
|
|
54 |
|
|
|
|
|
|
54 |
|
|
54 |
|
9 |
3. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
15 |
3 |
15 |
3 |
|
|
|
( 15 |
3)( |
15 |
|
3) |
|
|
15 |
9 |
|
6 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ɉɬɜɟɬ 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
Ȼɚɥɥɵ |
|||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ ɜɟɪɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
2 |
|
|||||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
1 |
|
|||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||
Ʉɨɦɦɟɧɬ |
ɢɣ. Ɉɲɢɛɤɢ ɜ ɩɪɢɦɟɧɟɧɢɢ ɮɨɪɦɭɥ; |
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
2 |
|
|||||||||||||||||||
ɫɱɢɬɚɸɬɫɹ ɫɭɳɟɫɬɜɟɧɧɵɦɢ ɩɪɢ ɢɯ |
|||||||||||||||||||||||||||||
ɧɚɥɢɱɢɢ ɪɟɲɟɧɢɟ ɧɟ ɡɚɫɱɢɬɵɜɚɟɬɫɹ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
22 |
|
Ɉɞɢɧ ɢɡ ɤɨɪɧɟɣ ɭɪɚɜɧɟɧɢɹ 5X2 |
2X ɇɚɣɞɢɬɟ3P1. 0 ɪɚɜɟɧ |
|
|
|
ɜɬɨɪɨɣ ɤɨɪɟɧɶ. |
|
|||||||||||||||||||||
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ɉɨɞɫɬɚɜɢɦ |
ɢɡɜɟɫɬɧɵɣ |
ɤɨɪɟɧɶ |
ɜ |
ɭɪɚɜɧɟɧɢɟ: |
5 |
|
|
2 3P 0. |
ɉɨɥɭɱɢɦ |
ɭɪɚɜɧɟɧɢɟ |
|||||||||||||||||||
ɨɬɧɨɫɢɬɟɥɶɧɨ P |
Ɋɟɲɢɦ: |
ɟɝɨ |
3P |
3; |
P |
1. |
ɉɨɞɫɬɚɜɢɦ |
|
P ɜ |
ɭɪɚɜɧɟɧɢɟ: |
|||||||||||||||||||
5X2 2X 3 |
0, ɨɬɤɭɞɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
X |
2 r |
4 |
|
4 5 3 |
|
|
2 r 8 |
, |
X |
1, X |
0,6. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
10 |
|
10 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ɉɬɜɟɬ |
0, 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
Ȼɚɥɥɵ |
|||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
|
|
3 |
|
||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
2 |
|
|||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ⱦɪɭɝɢɟɭɤɚɡɚɧɧɵɦɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ |
|
|
|
|
|
|
ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
3 |
|
||||||
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
2 |
23ɇɚɣɞɢɬɟ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ ɜɵɪɚɠɟɧɢɹ ɢ ɡɧɚɱɟɧɢɹ X ɢ, Y ɩɪɢ ɤɨɬɨɪɵɯ ɨɧɨ ɞɨɫɬɢɝɚɟɬɫɹ: 3X 4Y 2
 X 5Y 3.
X 5Y 3.
Ɋɟɲɟɧɢɟ
ɋɭɦɦɚ |
|
3X 4Y 2 |
|
|
|
X 5Y |
3 |
|
ɩɪɢɧɢɦɚɟɬ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ0, , ɪɚɜɧɨɟ |
ɬɨɥɶɤɨ ɜ |
||||||
|
|
|
|
|||||||||||||
ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɨɛɚ ɫɥɚɝɚɟɦɵɯ ɨɞɧɨɜɪɟɦɟɧɧɨ0. |
ɪɚɜɧɵ |
ɉɨɥɭɱɚɟɦ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
®X3 |
Y4 |
2 |
0, |
|
|
|
Ɋɟɲɢɦ: |
ɟɺ |
|
|
|
¯ X |
Y5 |
3 |
0. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
X3 |
4Y |
2 0, |
Y 11 |
11 0, |
Y |
1, |
|
|||||
|
® |
|
|
|
|
® |
|
|
® |
|
|
|||||
Ɉɬɜɟɬ |
|
|
|
¯X3 Y |
15 |
|
|
9 0, |
¯ |
X Y5 |
3 0, |
¯ X |
2. |
|
||
0; (2;1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
Ȼɚɥɥɵ |
||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
4 |
|||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
3 |
|||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
4 |
|
Ɇɨɞɭɥɶ "Ƚɟɨɦɟɬɪɢɹ"
24ɇɚɣɞɢɬɟ ɜɟɥɢɱɢɧɭ ɭɝɥɚ, COE ɟɫɥɢ OE – ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ AOC, OD – ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ COB.
Ɋɟɲɟɧɢɟ
COB=2·35°=70°;AOC =180°–70°=110°; ɋOE=110°:2=55°.
Ɉɬɜɟɬ 55°.
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
|
|
|
|
|
3 |
|
|||
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
Ȼɚɥɥɵ |
|||||
Ɋɟɲɟɧɢɟ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
2 |
|
||||
Ⱦɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ, ɢɥɢ ɨɩɢɫɤɚ ɫ ɟɺ ɭɱɟɬɨɦ |
1 |
|
||||||||
ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
0 |
|
||||||
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
2 |
|
||
25 |
ȼ |
ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɟ ABCD ɬɨɱɤɚ K — |
ɫɟɪɟɞɢɧɚ. ɫɬɨɪɨɧɵ |
AB ɂɡɜɟɫɬɧɨ, ɱɬɨ |
||||||
|
KC KD. Ⱦɨɤɚɠɢɬɟ, ɱɬɨ ɞɚɧɧɵɣ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦ — ɩɪɹɦɨɭɝɨɥɶɧɢɤ. |
|
|
|||||||
ɉɭɫɬɶ– |
ɬɨɱɤɚ K |
ɫɟɪɟɞɢɧɚ ɫɬɨɪɨɧɵ– |
AB ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ ABCD |
ɪɚɜɧɨɭɞɚɥɟɧɚ ɨɬ ɟɝɨ |
|
|||||
ɜɟɪɲɢɧ C ,ɢ D. |
Ɍɨɝɞɚ ɬɪɟɭɝɨɥɶɧɢɤ, |
CKD – ɪɚɜɧɨɛɟɞɪɟɧɧɵɣ |
ɩɨɷɬɨɦɭ KCD |
KDC. |
||||||
ɉɨɫɤɨɥɶɤɭ ɩɪɹɦɚɹ CD ɩɚɪɚɥɥɟɥɶɧɚ, |
ɫɬɨɪɨɧɟ AB ɬɨ BKC |
KCD ɢ AKD |
KDC |
|||||||
ɤɚɤ .ɧɚɤɪɟɫɬ ɥɟɠɚɳɢɟ |
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, +BKC |
+AKD ɩɨ ɩɟɪɜɨɦɭ ɩɪɢɡɧɚɤɭ ɪɚɜɟɧɫɬɜɚ |
||||||||
ɬɪɟɭɝɨɥɶɧɢɤɨɜ ( BKC |
AKD, AK BK, KC |
KD). |
|
|
|
|
||||
Ɂɧɚɱɢɬ, CBK |
DAK. ɂɯ ɫɭɦɦɚ ɪɚɜɧɚ, |
180q |
ɬ.,ɤ. ɷɬɨ ɞɜɚ ɭɝɥɚ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ |
|||
ɩɪɢɥɟɠɚɳɢɟ ɤ ɨɞɧɨɣ, |
ɫɬɨɪɨɧɟ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ |
CBK DAK |
90 . ɉɨ ɫɜɨɣɫɬɜɭ |
|||
ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ ɭɝɥɵ BCD ɢ CDA ɬɚɤɠɟ ɩɪɹɦɵɟ. |
Ɂɧɚɱɢɬ, ABCD – ɩɪɹɦɨɭɝɨɥɶɧɢɤ. |
|||||
Ʉɨɦɦɟɧɬ ɢɣ: |
Ɋɚɜɟɧɫɬɜɨ ɬɪɟɭɝɨɥɶɧɢɤɨɜ |
BKC ɢ |
AKD ɦɨɠɟɬ ɛɵɬɶ |
ɞɨɤɚɡɚɧɨ, |
ɢɧɚɱɟ |
|
ɧɚɩɪɢɦɟɪ, ɩɨ ɬɪɟɬɶɟɦɭ ɩɪɢɡɧɚɤɭ ɪɚɜɟɧɫɬɜɚ ɬɪɟɭɝɨɥɶɧɢɤɨɜ. |
|
|
||||
Ⱦ ɭɝɨɟ ɜɨɡɦɨɠɧɨɟ ɞɨɤ ɡ ɬɟɥɶɫɬɜɨ:
ɉɭɫɬɶ ɬɨɱɤɚ O – ɫɟɪɟɞɢɧɚ CD. ɑɟɬɵɪɟɯɭɝɨɥɶɧɢɤ OKBC ɹɜɥɹɟɬɫɹ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɨɦ,
ɩɨɫɤɨɥɶɤɭ ɟɝɨ |
ɫɬɨɪɨɧɵ |
OC ɢ |
KB ɩɚɪɚɥɥɟɥɶɧɵ |
ɢ ɪɚɜɧɵ. Ɍɪɟɭɝɨɥɶɧɢɤ KCD – |
||
ɪɚɜɧɨɛɟɞɪɟɧɧɵɣ, ɩɨɷɬɨɦɭ |
OK – |
ɟɝɨ ɜɵɫɨɬɚ. |
Ɂɧɚɱɢɬ, OKBC – ɩɪɹɦɨɭɝɨɥɶɧɢɤ, |
|||
ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɭɝɨɥ CBK – ɩɪɹɦɨɣ. |
|
|
||||
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
|||||
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ, |
ɜɟɪɧɨɟ ɜɫɟ ɲɚɝɢ ɨɛɨɫɧɨɜɚɧɵ |
|
3 |
|||
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ ɫɨɞɟɪɠɢɬ ɧɟɬɨɱɧɨɫɬɢ ɢɥɢ ɩɪɨɛɟɥɵ, ɧɚɩɪɢɦɟɪ, ɨɬɫɭɬɫɬɜɭɸɬ |
2 |
|||||
ɫɫɵɥɤɢ ɧɚ ɫɜɨɣɫɬɜɚ ɩɚɪɚɥɥɟɥɶɧɵɯ ɩɪɹɦɵɯ ɢɥɢ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ |
||||||
|
||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
0 |
|||||
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
3 |
|
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
4 |
26 Ɉɫɧɨɜɚɧɢɟ AC ɪɚɜɧɨɛɟɞɪɟɧɧɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ABC12. ɪɚɜɧɨ |
Ɉɤɪɭɠɧɨɫɬɶ |
ɪɚɞɢɭɫɚ 8 ɫ ɰɟɧɬɪɨɦ ɜɧɟ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɤɚɫɚɟɬɫɹ ɩɪɨɞɨɥɠɟɧɢɹ ɛɨɤɨɜɵɯ ɫɬɨɪɨɧ ɬɪɟɭɝɨɥɶɧɢɤɚ ɢ ɤɚɫɚɟɬɫɹ ɨɫɧɨɜɚɧɢɹ AC ɜ ɟɝɨ ɫɟɪɟɞɢɧɟ. ɇɚɣɞɢɬɟ ɪɚɞɢɭɫ
ɨɤɪɭɠɧɨɫɬɢ, ɜɩɢɫɚɧɧɨɣ ɜ ɬɪɟɭɝɨɥɶɧɢɤ ABC.
Ɋɟɲɟɧɢɟ
Ⱦɚɧɧɚɹ ɨɤɪɭɠɧɨɫɬɶ ɤɚɫɚɟɬɫɹ ɫɬɨɪɨɧɵ AC ɜ ɟɺ ɫɟɪɟɞɢɧɟ M ɢ ɩɪɨɞɨɥɠɟɧɢɣ ɫɬɨɪɨɧ BA ɢ BC ɬɪɟɭɝɨɥɶɧɢɤɚ ABC
—ɉɭɫɬɶ O |
ɰɟɧɬɪ, |
ɷɬɨɣ ɨɤɪɭɠɧɨɫɬɢ ɚ Q—, |
ɰɟɧɬɪ ɨɤɪɭɠɧɨɫɬɢ ɜɩɢɫɚɧɧɨɣ ɜ |
ɬɪɟɭɝɨɥɶɧɢɤ ABC ɍɝɨɥ OAQ – ɩɪɹɦɨɣ ɤɚɤ ɭɝɨɥ ɦɟɠɞɭ ɛɢɫɫɟɤɬɪɢɫɚɦɢ ɫɦɟɠɧɵɯ ɭɝɥɨɜ. Ɍɪɟɭɝɨɥɶɧɢɤ OAQ – ɩɪɹɦɨɭɝɨɥɶɧɵɣ, AM – ɟɝɨ ɜɵɫɨɬɚ. ɂɡ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɧɚɯɨɞɢɦ,
ɱɬɨ AM, 2 MQ MO. ɋɥɟɞɨɜɚɬɟɥɶɧɨ QM |
|
AM2 |
|
9 |
|
4,5. |
|
||
|
OM |
2 |
|
|
|||||
Ɉɬɜɟɬ 4, 5. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
|||||||
ɏɨɞ ɪɟɲɟɧɢɹ ɜɟɪɧɵɣ, ɜɫɟ ɟɝɨ ɲɚɝɢ ɜɵɩɨɥɧɟɧɵ ɩɪɚɜɢɥɶɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ |
4 |
||||||||
ɨɬɜɟɬ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
ɏɨɞ ɪɟɲɟɧɢɹ, |
ɜɟɪɧɵɣ ɜɫɟ ɟɝɨ ɲɚɝɢ |
ɜɵɩɨɥɧɟɧɵ |
ɩɪɚɜɢɥɶɧɨ, ɧɨ ɞɚɧɵ |
3 |
|||||
ɧɟɩɨɥɧɵɟ ɨɛɴɹɫɧɟɧɢɹ ɢɥɢ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɜɵɱɢɫɥɢɬɟɥɶɧɚɹ ɨɲɢɛɤɚ |
|||||||||
|
|||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɜɵɲɟ ɤɪɢɬɟɪɢɹɦ |
0 |
||||||||
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
4 |
|
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 3 |
1 |
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɡɚɞɚɧɢɣ ɫ ɪɚɡɜɺɪɧɭɬɵɦ ɨɬɜɟɬɨɦ |
|
Ɇɨɞɭɥɶ "Ⱥɥɝɟɛɪɚ"
21 |
|
ɍɩɪɨɫɬɢɬɟ ɜɵɪɚɠɟɧɢɟ |
|
|
|
15 |
3 |
15 |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
15 |
3 |
15 |
3 |
|
|
( |
|
15 |
3)( |
15 |
|
3) |
|
|
|
15 9 |
|
|
6 |
|
|
1 |
|
|
1 |
. |
|
|||||||||
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
24 |
|
24 |
|
|
|
4 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ɉɬɜɟɬ |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
|
|
|
|
Ȼɚɥɥɵ |
|||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ ɜɟɪɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
1 |
|
||||||||||||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||||||||||
Ʉɨɦɦɟɧɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ |
ɛ ɥɥ |
2 |
|
||||||||||||||||
. Ɉɲɢɛɤɢ ɜ ɩɪɢɦɟɧɟɧɢɢ ɮɨɪɦɭɥ; |
ɫɱɢɬɚɸɬɫɹ ɫɭɳɟɫɬɜɟɧɧɵɦɢ ɩɪɢ ɢɯ |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ɧɚɥɢɱɢɢ ɪɟɲɟɧɢɟ ɧɟ ɡɚɫɱɢɬɵɜɚɟɬɫɹ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
22 |
|
Ɉɞɢɧ ɢɡ ɤɨɪɧɟɣ ɭɪɚɜɧɟɧɢɹ 4X2 |
X |
3M |
|
0 ɪɚɜɟɧɇɚɣɞɢɬɟ1. |
|
|
ɜɬɨɪɨɣ ɤɨɪɟɧɶ. |
|
||||||||||||||||||||||||||||
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ɉɨɞɫɬɚɜɢɦ |
ɢɡɜɟɫɬɧɵɣ |
ɤɨɪɟɧɶ |
|
ɜ ɭɪɚɜɧɟɧɢɟ: |
4 |
|
|
1 3M 0. |
|
ɉɨɥɭɱɢɦ |
ɭɪɚɜɧɟɧɢɟ |
|||||||||||||||||||||||||||
ɨɬɧɨɫɢɬɟɥɶɧɨ M |
Ɋɟɲɢɦ |
ɟɝɨ: |
3M |
|
3; M |
1. |
|
ɉɨɞɫɬɚɜɢɦ: M |
ɜ |
ɭɪɚɜɧɟɧɢɟ |
||||||||||||||||||||||||||||
4X2 X |
3 |
|
0, ɨɬɤɭɞɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
X |
1 r 1 4 3 4 |
|
1 r 7 |
, X |
|
1, X |
3 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
8 |
|
1 |
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ɉɬɜɟɬ |
|
. |
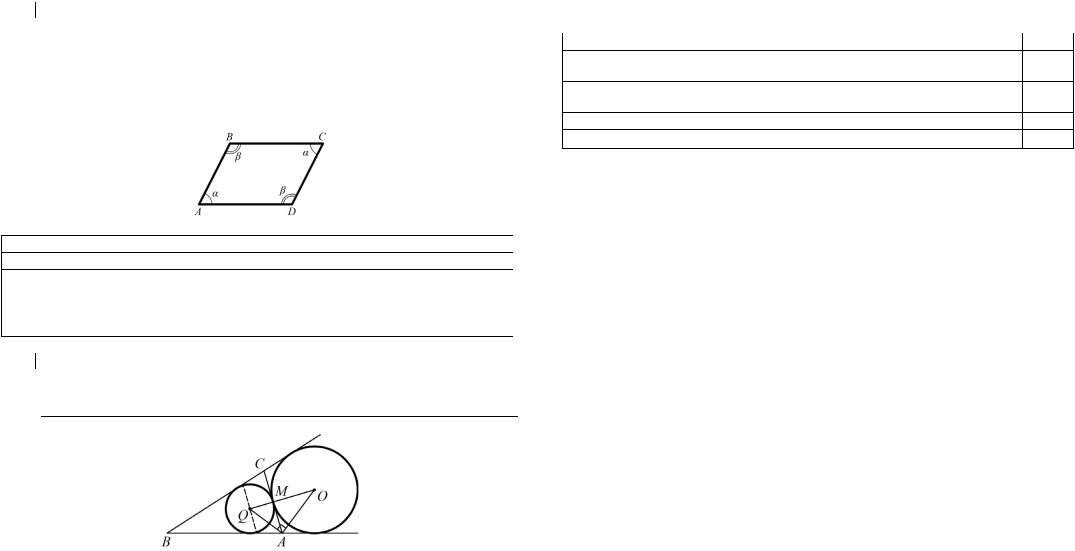
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
|
|
|
|
Ȼɚɥɥɵ |
|||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
2 |
|
||||||||||||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ |
ɛ ɥɥ |
3 |
|
||||||||||
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 3 |
2 |
23ɇɚɣɞɢɬɟ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ ɜɵɪɚɠɟɧɢɹ ɢ ɡɧɚɱɟɧɢɹ X ɢ Y, ɩɪɢ ɤɨɬɨɪɵɯ ɨɧɨ ɞɨɫɬɢɝɚɟɬɫɹ 6X Y 5
 3X 2Y 1.
3X 2Y 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ɋɭɦɦɚ |
|
6X Y 5 |
|
|
|
3X |
2Y 1 |
|
ɩɪɢɧɢɦɚɟɬ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ0, , |
ɪɚɜɧɨɟ |
ɬɨɥɶɤɨ ɜ |
|||||||||
|
|
|
|
|||||||||||||||||
ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɨɛɚ ɫɥɚɝɚɟɦɵɯ ɨɞɧɨɜɪɟɦɟɧɧɨ0. |
ɪɚɜɧɵ |
ɉɨɥɭɱɚɟɦ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
®X6 |
Y |
5 |
0, |
|
|
|
|
|
|
Ɋɟɲɢɦ ɟɺ |
|
|
|
|
|
¯X3 |
2Y |
1 |
0. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
X6 |
|
Y 5 0, |
Y3 |
3 0, |
|
|
Y 1, |
Y 1, |
|
|
|||||||
® |
|
|
|
|
|
|
|
® |
|
|
® |
|
|
® |
|
|
|
|||
|
|
|
¯X6 Y4 |
2 0, |
¯X6 |
Y 5 0, ¯ |
6X |
6 0, |
¯ X |
1. |
|
|
||||||||
Ɉɬɜɟɬ 0; (–1;1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
Ȼɚɥɥɵ |
||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
4 |
|
|||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
3 |
|
||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺɞɨɜɟɞɟɧɨɭɱɺɬɨɦ ɪɟɲɟɧɢɟ |
|
ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ ɛ ɥɥ |
4 |
|
||
Ɇɨɞɭɥɶ "Ƚɟɨɦɟɬɪɢɹ"
24ɇɚɣɞɢɬɟ ɜɟɥɢɱɢɧɭ ɭɝɥɚ COE, ɟɫɥɢ OE – ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ AOC, OD – ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ COB.
Ɋɟɲɟɧɢɟ |
|
|
|
=2·32°=64°;COB |
=180°–64°=116°; =116°:2=58°ɋOE |
. |
|
Ɉɬɜɟɬ 58°. |
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
|
Ɋɟɲɟɧɢɟ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
2 |
Ⱦɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɟɬɨɦ |
1 |
||
ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
||
|
|
||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
0 |
||
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ ɛ ɥɥ |
2 |
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 3 |
3 |
25ɉɪɨɬɢɜɨɩɨɥɨɠɧɵɟ ɭɝɥɵ ɱɟɬɵɪɟɯɭɝɨɥɶɧɢɤɚ ɩɨɩɚɪɧɨ. ɪɚɜɧɵ Ⱦɨɤɚɠɢɬɟ, ɱɬɨ ɷɬɨɬ ɱɟɬɵɪɟɯɭɝɨɥɶɧɢɤ – ɩɚɪɚɥɥɟɥɨɝɪɚɦɦ.
ɉɭɫɬɶ |
ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɟ |
ɭɝɥɵ |
A ɢ |
C ɱɟɬɵɪɟɯɭɝɨɥɶɧɢɤɚ |
ABCD, |
ɪɚɜɧɵ |
Į |
ɚ |
|
|
ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɟ ɭɝɥɵ |
B ɢ |
.D ɪɚɜɧɵ |
ȕ ɉɨɫɤɨɥɶɤɭ |
ɫɭɦɦɚ |
ɭɝɥɨɜ |
ɥɸɛɨɝɨ |
||||
ɱɟɬɵɪɟɯɭɝɨɥɶɧɢɤɚ ,ɪɚɜɧɚ 360q ɬɨ 2Į |
2ȕ |
360q. Ɂɧɚɱɢɬ, Į |
ȕ 180q. |
Ɍɚɤ ɤɚɤ ɫɭɦɦɚ |
||||||
ɜɧɭɬɪɟɧɧɢɯ ɨɞɧɨɫɬɨɪɨɧɧɢɯ ɭɝɥɨɜ ɩɪɢ ɫɟɤɭɳɟɣ ɪɚɜɧɚ180 ,ɬɨ ɩɨ ɩɪɢɡɧɚɤɭ ɩɚɪɚɥɥɟɥɶɧɵɯ ɩɪɹɦɵɯ AB ɩɚɪɚɥɥɟɥɶɧɚ CD, BC ɩɚɪɚɥɥɟɥɶɧɚ AD. Ɂɧɚɱɢɬ, ɱɟɬɵɪɺɯɭɝɨɥɶɧɢɤ ABCD ɹɜɥɹɟɬɫɹ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɨɦ ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ.
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 3 |
|
4 |
||
Ɉɬɜɟɬ |
8 |
. |
|
|
|
|
|
||
3 |
|
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
Ȼɚɥɥɵ |
ɏɨɞ ɪɟɲɟɧɢɹ ɜɟɪɧɵɣ, ɜɫɟ ɟɝɨ ɲɚɝɢ ɜɵɩɨɥɧɟɧɵ ɩɪɚɜɢɥɶɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ |
4 |
|||
ɨɬɜɟɬ |
|
|||
|
|
|||
ɏɨɞ ɪɟɲɟɧɢɹ ɜɟɪɧɵɣ, ɜɫɟ ɟɝɨ ɲɚɝɢ ɜɵɩɨɥɧɟɧɵ ɩɪɚɜɢɥɶɧɨ, ɧɨ |
ɞɚɧɵ |
3 |
||
ɧɟɩɨɥɧɵɟ ɨɛɴɹɫɧɟɧɢɹ ɢɥɢ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɜɵɱɢɫɥɢɬɟɥɶɧɚɹ ɨɲɢɛɤɚ |
|
|||
|
|
|||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɜɵɲɟ ɤɪɢɬɟɪɢɹɦ |
|
0 |
||
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ |
ɛ ɥɥ |
4 |
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
||
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ, |
ɜɟɪɧɨɟ ɜɫɟ ɲɚɝɢ ɨɛɨɫɧɨɜɚɧɵ |
3 |
|
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ ɫɨɞɟɪɠɢɬ ɧɟɬɨɱɧɨɫɬɢ ɢɥɢ ɩɪɨɛɟɥɵ, ɧɚɩɪɢɦɟɪ, ɨɬɫɭɬɫɬɜɭɸɬ |
2 |
||
ɫɫɵɥɤɢ ɧɚ ɫɜɨɣɫɬɜɚ ɩɚɪɚɥɥɟɥɶɧɵɯ ɩɪɹɦɵɯ ɢɥɢ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ |
|||
|
|||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
0 |
||
|
Ɇ ɤɫ ɦ ɥɶɧɵ ɛ ɥɥ |
3 |
|
26 |
Ɉɫɧɨɜɚɧɢɟ AC ɪɚɜɧɨɛɟɞɪɟɧɧɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ABC8. ɪɚɜɧɨ |
Ɉɤɪɭɠɧɨɫɬɶ |
|
ɪɚɞɢɭɫɚ 6 ɫ ɰɟɧɬɪɨɦ ɜɧɟ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɤɚɫɚɟɬɫɹ ɩɪɨɞɨɥɠɟɧɢɹ ɛɨɤɨɜɵɯ |
|
|
ɫɬɨɪɨɧ ɬɪɟɭɝɨɥɶɧɢɤɚ ɢ ɤɚɫɚɟɬɫɹ ɨɫɧɨɜɚɧɢɹ AC ɜ ɟɝɨ ɫɟɪɟɞɢɧɟ. ɇɚɣɞɢɬɟ ɪɚɞɢɭɫ |
|
, |
ɨɤɪɭɠɧɨɫɬɢ ɜɩɢɫɚɧɧɨɣ ɜ ɬɪɟ. ɭɝɨɥɶɧɢɤ ABC |
|
Ɋɟɲɟɧɢɟ
Ⱦɚɧɧɚɹ ɨɤɪɭɠɧɨɫɬɶ ɤɚɫɚɟɬɫɹ ɫɬɨɪɨɧɵ AC ɜ ɟɺ ɫɟɪɟɞɢɧɟ M ɢ ɩɪɨɞɨɥɠɟɧɢɣ ɫɬɨɪɨɧ BA BC ɬɪɟɭɝɨɥɶɧɢɤɚ ABC.
– ɉɭɫɬɶ O ,ɰɟɧɬɪ ɷɬɨɣ ɨɤɪɭɠɧɨɫɬɢ ɚ, Q– |
ɰɟɧɬɪ ɨɤɪɭɠɧɨɫɬɢ ɜɩɢɫɚɧɧɨɣ ɜ ɬɪɟɭɝɨɥɶɧɢɤ |
||||||
ABC. ɍɝɨɥ OAQ – ɩɪɹɦɨɣ ɤɚɤ ɭɝɨɥ ɦɟɠɞɭ ɛɢɫɫɟɤɬɪɢɫɚɦɢ ɫɦɟɠɧɵɯ. |
ɭɝɥɨɜ Ɍɪɟɭɝɨɥɶɧɢɤ |
||||||
OAQ – |
ɩɪɹɦɨɭɝɨɥɶɧɵɣ, AM –. ɟɝɨ ɜɵɫɨɬɚ |
ɂɡ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɧɚɯɨɞɢɦ, ɱɬɨ |
|||||
AM2 |
MQ MO. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, QM |
AM2 |
|
|
8 |
. |
|
OM |
3 |
|
|||||
|
|
|
|
||||
© ɆɂɈɈ 2012 |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 4 |
1 |
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɡɚɞɚɧɢɣ ɫ ɪɚɡɜɺɪɧɭɬɵɦ ɨɬɜɟɬɨɦ |
|
Ɇɨɞɭɥɶ "Ⱥɥɝɟɛɪɚ"
21 |
|
ɍɩɪɨɫɬɢɬɟ ɜɵɪɚɠɟɧɢɟ |
|
|
|
|
|
54 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
31 |
5 |
|
31 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
54 |
|
|
|
|
|
|
|
|
|
54 |
|
|
|
|
|
54 |
|
|
54 |
|
9 |
3. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
31 |
5 |
31 |
5 |
|
|
|
( 31 |
5)( |
31 |
|
5) |
|
|
31 |
25 |
|
6 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ɉɬɜɟɬ 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
Ȼɚɥɥɵ |
|||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ ɜɟɪɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
2 |
|
|||||||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
1 |
|
|||||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||
Ʉɨɦɦɟɧɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ |
ɛ ɥɥ |
2 |
|
||||||||
. Ɉɲɢɛɤɢ ɜ ɩɪɢɦɟɧɟɧɢɢ ɮɨɪɦɭɥ ɫɱɢɬɚɸɬɫɹ ɫɭɳɟɫɬɜɟɧɧɵɦɢ; ɩɪɢ ɢɯ |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ɧɚɥɢɱɢɢ ɪɟɲɟɧɢɟ ɧɟ ɡɚɫɱɢɬɵɜɚɟɬɫɹ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
22 |
|
Ɉɞɢɧ ɢɡ ɤɨɪɧɟɣ ɭɪɚɜɧɟɧɢɹ 5X2 |
7X |
2M 0 ɪɚɜɟɧ –1. ɇɚɣɞɢɬɟ ɜɬɨɪɨɣ ɤɨɪɟɧɶ. |
|
||||||||||||||||||||||||||
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ɉɨɞɫɬɚɜɢɦ ɢɡɜɟɫɬɧɵɣ |
ɤɨɪɟɧɶ: |
|
ɜ |
ɭɪɚɜɧɟɧɢɟ |
5 |
|
|
7 2M 0. |
ɉɨɥɭɱɢɦ |
ɭɪɚɜɧɟɧɢɟ |
|||||||||||||||||||||
ɨɬɧɨɫɢɬɟɥɶɧɨ |
|
M |
Ɋɟɲɢɦ ɟɝɨ: |
2M |
2; |
M |
1. |
|
|
ɉɨɞɫɬɚɜɢɦ |
|
M |
ɜ |
ɭɪɚɜɧɟɧɢɟ: |
|||||||||||||||||
5X2 |
7X |
2 |
0, ɨɬɤɭɞɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
X |
|
7 r |
49 |
|
|
4 5 2 |
|
|
7 r 3 |
, |
X |
1, |
X |
0,4. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
10 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|||||
Ɉɬɜɟɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0, 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
Ȼɚɥɥɵ |
|||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
3 |
|
||||||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
2 |
|
|||||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Ⱦɪɭɝɢɟɭɤɚɡɚɧɧɵɦɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ |
|
|
ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
0 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ |
ɛ ɥɥ |
3 |
|
|||||
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 4 |
2 |
23ɇɚɣɞɢɬɟ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ ɜɵɪɚɠɟɧɢɹ ɢ ɡɧɚɱɟɧɢɹ X ɢ Y, ɩɪɢ ɤɨɬɨɪɵɯ ɨɧɨ ɞɨɫɬɢɝɚɟɬɫɹ: 3X 4Y 1
 X 5Y 6.
X 5Y 6.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ɋɭɦɦɚ |
|
3X 4Y 1 |
|
|
|
X |
5Y |
6 |
|
ɩɪɢɧɢɦɚɟɬ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ0, , ɪɚɜɧɨɟ |
ɬɨɥɶɤɨ ɜ |
||||||||
|
|
|
|
||||||||||||||||
ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɨɛɚ ɫɥɚɝɚɟɦɵɯ ɨɞɧɨɜɪɟɦɟɧɧɨ0. |
ɪɚɜɧɵ |
ɉɨɥɭɱɚɟɦ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
®X3 |
Y4 |
1 |
0, |
|
|
|
|
Ɋɟɲɢɦ ɟɺ |
|
|
|
|
¯ X |
Y5 |
6 |
0. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
X3 |
Y4 |
1 |
0, |
19Y |
19 0, |
Y |
1, |
|
|
|||||
® |
|
|
|
|
|
|
® |
|
|
® |
|
|
|
||||||
|
|
|
|
|
¯X3 |
15Y 18 0; |
¯ |
X Y5 |
6 0; |
¯ X |
1. |
|
|
||||||
Ɉɬɜɟɬ 0; (–1;1). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
Ȼɚɥɥɵ |
||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
4 |
|
|||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
3 |
|
|||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ ɛ ɥɥ |
4 |
|
|
Ɇɨɞɭɥɶ "Ƚɟɨɦɟɬɪɢɹ"
24ɇɚɣɞɢɬɟ ɜɟɥɢɱɢɧɭ ɭɝɥɚ, DOB ɟɫɥɢ OE – ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ, AOC– OD ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ COB.
Ɋɟɲɟɧɢɟ
COȺ=2·64°=128°; ȼOC=180°–128°=52°;DOB =52°:2=26°.
Ɉɬɜɟɬ 26°. |
|
||
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
|
Ɋɟɲɟɧɢɟ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
2 |
|
Ⱦɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ, ɢɥɢ ɨɩɢɫɤɚ ɫ ɟɺ ɭɱɟɬɨɦ |
1 |
||
ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|||
|
|||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
0 |
||
|
Ɇ ɤɫ ɦ ɥɶɧɵ ɛ ɥɥ |
2 |
|
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 4 |
3 |
25ɋɟɪɟɞɢɧɚ ɫɬɨɪɨɧɵ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ ɪɚɜɧɨɭɞɚɥɟɧɚ ɨɬ ɤɨɧɰɨɜ ɟɝɨ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɣ. ɫɬɨɪɨɧɵ Ⱦɨɤɚɠɢɬɟ, ɱɬɨ ɞɚɧɧɵɣ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦ – ɩɪɹɦɨɭɝɨɥɶɧɢɤ.
ɉɭɫɬɶ– |
ɬɨɱɤɚ O ɫɟɪɟɞɢɧɚ ɫɬɨɪɨɧɵ– |
BC ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ ABCD ɪɚɜɧɨɭɞɚɥɟɧɚ ɨɬ ɟɝɨ |
|
||||||
ɜɟɪɲɢɧ A ɢ D.Ɍɨɝɞɚ ɬɪɟɭɝɨɥɶɧɢɤ, |
AOD ɪɚɜɧɨɛɟɞɪɟɧɧɵɣ |
ɩɨɷɬɨɦɭ |
AOD |
ODA. |
|||||
ɉɨɫɤɨɥɶɤɭ ɩɪɹɦɚɹ ȼɋ ɩɚɪɚɥɥɟɥɶɧɚ, |
ɫɬɨɪɨɧɟ AD ɬɨ ɭɝɥɵ BOA ɢ COD ɪɚɜɧɵ ɭɤɚɡɚɧɧɵɦ |
||||||||
ɭɝɥɚɦ ɤɚɤ ɧɚɤɪɟɫɬ. |
ɥɟɠɚɳɢɟ Ɍɚɤɢɦ |
ɨɛɪɚɡɨɦ, |
BOA |
COD ɩɨ ɩɟɪɜɨɦɭ |
ɩɪɢɡɧɚɤɭ |
||||
ɪɚɜɟɧɫɬɜɚ ɬɪɟɭɝɨɥɶɧɢɤɨɜ. Ɂɧɚɱɢɬ, ABO ODA.ɉɭɫɬɶ ɢɯ ɜɟɥɢɱɢɧɚ. |
ɪɚɜɧɚ Į ɉɪɹɦɵɟ |
||||||||
AB ɢ CD ɩɚɪɚɥɥɟɥɶɧɵ, ɩɨɷɬɨɦɭ Į |
Į |
180q, ɬ..ɟ Į |
90. q ɉɨ ɫɜɨɣɫɬɜɭ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ |
||||||
ɭɝɥɵ BAD ɢ CDA. ɬɚɤɠɟ ɩɪɹɦɵɟ Ɂɧɚɱɢɬ, ABCD – ɩɪɹɦɨɭɝɨɥɶɧɢɤ. |
|
|
|
||||||
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
||
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ, |
ɜɟɪɧɨɟ ɜɫɟ ɲɚɝɢ ɨɛɨɫɧɨɜɚɧɵ |
3 |
|
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ ɫɨɞɟɪɠɢɬ ɧɟɬɨɱɧɨɫɬɢ ɢɥɢ ɩɪɨɛɟɥɵ, ɧɚɩɪɢɦɟɪ, ɨɬɫɭɬɫɬɜɭɸɬ |
2 |
||
ɫɫɵɥɤɢ ɧɚ ɫɜɨɣɫɬɜɚ ɩɚɪɚɥɥɟɥɶɧɵɯ ɩɪɹɦɵɯ ɢɥɢ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ |
|||
|
|||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
0 |
||
|
Ɇ ɤɫ ɦ ɥɶɧɵ ɛ ɥɥ |
3 |
|
26 Ɉɫɧɨɜɚɧɢɟ AC ɪɚɜɧɨɛɟɞɪɟɧɧɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ABC6. ɪɚɜɧɨ |
Ɉɤɪɭɠɧɨɫɬɶ |
ɪɚɞɢɭɫɚ 5 ɫ ɰɟɧɬɪɨɦ ɜɧɟ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɤɚɫɚɟɬɫɹ ɩɪɨɞɨɥɠɟɧɢɹ ɛɨɤɨɜɵɯ |
|
ɫɬɨɪɨɧ ɬɪɟɭɝɨɥɶɧɢɤɚ ɢ ɤɚɫɚɟɬɫɹ ɨɫɧɨɜɚɧɢɹ AC. ɜ ɟɝɨ ɫɟɪɟɞɢɧɟ |
ɇɚɣɞɢɬɟ ɪɚɞɢɭɫ |
ɨɤɪɭɠɧɨɫɬɢ, ɜɩɢɫɚɧɧɨɣ ɜ ɬɪɟɭɝɨɥɶɧɢɤ ABC.
Ɋɟɲɟɧɢɟ
Ⱦɚɧɧɚɹ ɨɤɪɭɠɧɨɫɬɶ ɤɚɫɚɟɬɫɹ ɫɬɨɪɨɧɵ AC ɜ ɟɺ ɫɟɪɟɞɢɧɟ M ɢ ɩɪɨɞɨɥɠɟɧɢɣ ɫɬɨɪɨɧ BA ɢ BC ɬɪɟɭɝɨɥɶɧɢɤɚ ABC.
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 4 |
|
|
|
|
|
|
|
|
4 |
|||
ɉɭɫɬɶ O — |
ɰɟɧɬɪ, |
ɷɬɨɣ ɨɤɪɭɠɧɨɫɬɢ |
ɚ Q ,— |
ɰɟɧɬɪ ɨɤɪɭɠɧɨɫɬɢ |
ɜɩɢɫɚɧɧɨɣ ɜ |
|||||||
ɬɪɟɭɝɨɥɶɧɢɤ ABC. ɍɝɨɥ– OAQ |
ɩɪɹɦɨɣ ɤɚɤ ɭɝɨɥ ɦɟɠɞɭ ɛɢɫɫɟɤɬɪɢɫɚɦɢ ɫɦɟɠɧɵɯ ɭɝɥɨɜ. |
|||||||||||
Ɍɪɟɭɝɨɥɶɧɢɤ, – |
OAQ – ɩɪɹɦɨɭɝɨɥɶɧɵɣ AM |
ɟɝɨ ɜɵɫɨɬɚ. ɂɡ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ, |
ɧɚɯɨɞɢɦ |
|||||||||
ɱɬɨ AM2 MQ MO. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, QM |
|
AM2 |
|
9 |
|
1, 8. |
|
|
||||
|
OM |
5 |
|
|
|
|||||||
Ɉɬɜɟɬ 1, 8. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
Ȼɚɥɥɵ |
||||||||
ɏɨɞ ɪɟɲɟɧɢɹ ɜɟɪɧɵɣ, ɜɫɟ ɟɝɨ ɲɚɝɢ ɜɵɩɨɥɧɟɧɵ ɩɪɚɜɢɥɶɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ |
4 |
|||||||||||
ɨɬɜɟɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɏɨɞ ɪɟɲɟɧɢɹ, |
ɜɟɪɧɵɣ ɜɫɟ |
ɟɝɨ ɲɚɝɢ |
ɜɵɩɨɥɧɟɧɵ |
ɩɪɚɜɢɥɶɧɨ, ɧɨ |
ɞɚɧɵ |
3 |
||||||
ɧɟɩɨɥɧɵɟ ɨɛɴɹɫɧɟɧɢɹ ɢɥɢ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɜɵɱɢɫɥɢɬɟɥɶɧɚɹ ɨɲɢɛɤɚ |
|
|||||||||||
|
|
|||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɜɵɲɟ ɤɪɢɬɟɪɢɹɦ |
|
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫ ɦ ɥɶɧɵ |
ɛ ɥɥ |
4 |
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 5 |
1 |
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɡɚɞɚɧɢɣ ɫ ɪɚɡɜɺɪɧɭɬɵɦ ɨɬɜɟɬɨɦ |
|
Ɇɨɞɭɥɶ "Ⱥɥɝɟɛɪɚ"
21 |
|
ɍɩɪɨɫɬɢɬɟ ɜɵɪɚɠɟɧɢɟ |
|
|
10 |
2 |
10 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
10 |
2 |
10 |
2 |
|
|
( |
|
10 |
|
2)( |
10 |
|
2) |
|
|
|
10 |
4 |
|
6 |
|
1 |
|
|
1 |
. |
|
||||
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
24 |
|
|
24 |
|
|
4 |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ɉɬɜɟɬ |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
|
Ȼɚɥɥɵ |
||||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ ɜɟɪɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
1 |
|
|||||||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
2 |
|
|||||||||
Ʉɨɦɦɟɧɬ |
ɢɣ. Ɉɲɢɛɤɢ ɜ ɩɪɢɦɟɧɟɧɢɢ ɮɨɪɦɭɥ ɫɱɢɬɚɸɬɫɹ ɫɭɳɟɫɬɜɟɧɧɵɦɢ; |
ɩɪɢ ɢɯ |
|||||||||||||||||||||||||||||||
ɧɚɥɢɱɢɢ ɪɟɲɟɧɢɟ ɧɟ ɡɚɫɱɢɬɵɜɚɟɬɫɹ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
22 |
|
Ɉɞɢɧ ɢɡ ɤɨɪɧɟɣ ɭɪɚɜɧɟɧɢɹ 5X2 |
|
2X ɇɚɣɞɢɬɟ3P1. 0 ɪɚɜɟɧ |
|
|
ɜɬɨɪɨɣ ɤɨɪɟɧɶ. |
|
|||||||||||||||||||||||||
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ɉɨɞɫɬɚɜɢɦ |
ɢɡɜɟɫɬɧɵɣ |
ɤɨɪɟɧɶ |
|
ɜ |
ɭɪɚɜɧɟɧɢɟ: |
5 |
|
|
2 3P 0. |
ɉɨɥɭɱɢɦ |
ɭɪɚɜɧɟɧɢɟ |
||||||||||||||||||||||
ɨɬɧɨɫɢɬɟɥɶɧɨ P |
Ɋɟɲɢɦ: |
ɟɝɨ |
3P |
|
3; P |
1. |
|
ɉɨɞɫɬɚɜɢɦ |
P |
ɜ |
ɭɪɚɜɧɟɧɢɟ: |
||||||||||||||||||||||
5X2 2X 3 |
0, ɨɬɤɭɞɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
X |
2 r |
4 4 5 3 |
|
|
2 r 8 |
, |
X |
1, X |
0,6. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
10 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ɉɬɜɟɬ |
0, 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
|
|
Ȼɚɥɥɵ |
|||||||||||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
|
|
|
3 |
|
|||||||||||||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
2 |
|
|||||||||||||||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɺɬɨɦ ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ⱦɪɭɝɢɟɭɤɚɡɚɧɧɵɦɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ |
|
|
|
|
|
ɤɪɢɬɟɪɢɹɦ |
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
3 |
|
|||||||||
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 5 |
2 |
23ɇɚɣɞɢɬɟ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ ɜɵɪɚɠɟɧɢɹ ɢ ɡɧɚɱɟɧɢɹ X ɢ Y, ɩɪɢ ɤɨɬɨɪɵɯ ɨɧɨ ɞɨɫɬɢɝɚɟɬɫɹ 6X Y 5
 3X 2Y 1.
3X 2Y 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ɋɭɦɦɚ |
|
6X Y 5 |
|
|
|
3X |
2Y 1 |
|
ɩɪɢɧɢɦɚɟɬ ɧɚɢɦɟɧɶɲɟɟ ɡɧɚɱɟɧɢɟ0, , |
ɪɚɜɧɨɟ |
ɬɨɥɶɤɨ ɜ |
|||||||||
|
|
|
|
|||||||||||||||||
ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɨɛɚ ɫɥɚɝɚɟɦɵɯ ɨɞɧɨɜɪɟɦɟɧɧɨ0. |
ɪɚɜɧɵ |
ɉɨɥɭɱɚɟɦ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
®X6 |
Y |
5 |
0, |
|
|
|
|
|
|
Ɋɟɲɢɦ ɟɺ |
|
|
|
|
|
¯X3 |
2Y |
1 |
0. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
X6 |
|
Y 5 0, |
Y3 |
3 0, |
|
|
Y 1, |
Y 1, |
|
|
|||||||
® |
|
|
|
|
|
|
|
® |
|
|
® |
|
|
® |
|
|
|
|||
|
|
|
¯X6 Y4 |
2 0, |
¯X6 |
Y 5 0, ¯ |
6X |
6 0, |
¯ X |
1. |
|
|
||||||||
Ɉɬɜɟɬ 0; (–1;1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
|
Ȼɚɥɥɵ |
||||||||||||||
ȼɫɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɜɵɩɨɥɧɟɧɵ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
|
|
4 |
|
|||||||||||||||
ɉɨ ɯɨɞɭ ɪɟɲɟɧɢɹ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ |
3 |
|
||||||||||||||||||
ɨɩɢɫɤɚ, ɫ ɟɺɞɨɜɟɞɟɧɨɭɱɺɬɨɦ ɪɟɲɟɧɢɟ |
|
ɞɨ ɤɨɧɰɚ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
4 |
|
||
Ɇɨɞɭɥɶ "Ƚɟɨɦɟɬɪɢɹ"
24ɇɚɣɞɢɬɟ ɜɟɥɢɱɢɧɭ ɭɝɥɚ DOB, ɟɫɥɢ OE – ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ, AOC– OD ɛɢɫɫɟɤɬɪɢɫɚ ɭɝɥɚ COB.
Ɋɟɲɟɧɢɟ
COȺ=2·64°=128°; ȼOC=180°–128°=52°;DOB =52°:2=26°.
Ɉɬɜɟɬ 26°. |
|
||
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
Ȼɚɥɥɵ |
|
Ɋɟɲɟɧɢɟ, |
ɜɟɪɧɨ ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ ɨɬɜɟɬ |
2 |
|
Ⱦɨɩɭɳɟɧɚ ɨɞɧɚ ɨɲɢɛɤɚ ɜɵɱɢɫɥɢɬɟɥɶɧɨɝɨ ɯɚɪɚɤɬɟɪɚ ɢɥɢ ɨɩɢɫɤɚ, ɫ ɟɺ ɭɱɟɬɨɦ |
1 |
||
ɪɟɲɟɧɢɟ ɞɨɜɟɞɟɧɨ ɞɨ ɤɨɧɰɚ |
|||
|
|||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
0 |
||
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
2 |
|
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 5 |
|
|
|
|
|
3 |
|
||||
25 ȼ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɟ ABCD ɬɨɱɤɚ M — ɫɟɪɟɞɢɧɚ. |
ɫɬɨɪɨɧɵ, AB ɂɡɜɟɫɬɧɨ ɱɬɨ |
||||||||||
|
MC |
MD. Ⱦɨɤɚɠɢɬɟ, ɱɬɨ ɞɚɧɧɵɣ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦ — ɩɪɹɦɨɭɝɨɥɶɧɢɤ. |
|
|
|||||||
ɉɭɫɬɶ |
ɬɨɱɤɚ Mɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ– ɫɟɪɟɞɢɧɚ ɫɬɨɪɨɧɵ AB |
|
|
ABCD – ɪɚɜɧɨɭɞɚɥɟɧɚ ɨɬ ɟɝɨ |
|
||||||
ɜɟɪɲɢɧ C ɢ D. Ɍɨɝɞɚ, ɬɪɟɭɝɨɥɶɧɢɤ CMD – ɪɚɜɧɨɛɟɞɪɟɧɧɵɣ, ɩɨɷɬɨɦɭ MCD |
MDC. |
||||||||||
ɉɨɫɤɨɥɶɤɭ |
ɩɪɹɦɚɹ |
CD ɩɚɪɚɥɥɟɥɶɧɚ |
, |
ɫɬɨɪɨɧɟ AB |
ɬɨ |
BMC |
MCD ɢ |
||||
AMD |
MDC ɤɚɤ |
ɧɚɤɪɟɫɬ ɥɟɠɚɳɢɟ. |
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, |
+BMC |
+AMD ɩɨ |
ɩɟɪɜɨɦɭ |
|||||
ɩɪɢɡɧɚɤɭ( |
ɪɚɜɟɧɫɬɜɚ ɬɪɟɭɝɨɥɶɧɢɤɨɜ BMC |
AMD, AM |
|
BM, MC MD). |
|
|
|||||
Ɂɧɚɱɢɬ, CBM |
DAM. ɂɯ ɫɭɦɦɚ ,ɪɚɜɧɚ 180q |
ɬ ɤ. ɷɬɨ ɞɜɚ ɭɝɥɚ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ, |
||||||||||
ɩɪɢɥɟɠɚɳɢɟ ɤ ɨɞɧɨɣ ɫɬɨɪɨɧɟ. |
ɋɥɟɞɨɜɚɬɟɥɶɧɨ, CBM |
DAM |
90 . ɉɨ ɫɜɨɣɫɬɜɭ |
|||||||||
ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ ɭɝɥɵ BCD ɢ CDA ɬɚɤɠɟ ɩɪɹɦɵɟ. Ɂɧɚɱɢɬ, ABCD – ɩɪɹɦɨɭɝɨɥɶɧɢɤ. |
||||||||||||
Ʉɨɦɦɟɧɬ |
ɢɣ: |
Ɋɚɜɟɧɫɬɜɨ |
ɬɪɟɭɝɨɥɶɧɢɤɨɜ BMC ɢ |
AMD ɦɨɠɟɬ |
ɛɵɬɶ |
ɞɨɤɚɡɚɧɨ |
ɢɧɚɱɟ, |
|||||
ɧɚɩɪɢɦɟɪ, ɩɨ ɬɪɟɬɶɟɦɭ ɩɪɢɡɧɚɤɭ ɪɚɜɟɧɫɬɜɚ ɬɪɟɭɝɨɥɶɧɢɤɨɜ. |
|
|
|
|
||||||||
Ⱦ ɭɝɨɟ ɜɨɡɦɨɠɧɨɟ ɞɨɤ ɡ ɬɟɥɶɫɬɜɨ: |
|
|
|
|
|
|
|
|||||
ɉɭɫɬɶ– |
ɬɨɱɤɚ O |
ɫɟɪɟɞɢɧɚ CD. ɑɟɬɵɪɟɯɭɝɨɥɶɧɢɤ OMBC ɹɜɥɹɟɬɫɹ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɨɦ, |
||||||||||
ɩɨɫɤɨɥɶɤɭ |
ɟɝɨ |
ɫɬɨɪɨɧɵ |
OC ɢ |
MB ɩɚɪɚɥɥɟɥɶɧɵ ɢ |
ɪɚɜɧɵ. |
Ɍɪɟɭɝɨɥɶɧɢɤ |
MCD – |
|||||
ɪɚɜɧɨɛɟɞɪɟɧɧɵɣ,– ɩɨɷɬɨɦɭ |
OM |
ɟɝɨ |
ɜɵɫɨɬɚ. |
Ɂɧɚɱɢɬ, |
OMBC– |
ɩɪɹɦɨɭɝɨɥɶɧɢɤ, |
||||||
ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɭɝɨɥ– .CBM ɩɪɹɦɨɣ |
|
|
|
|
|
|
|
|||||
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
Ȼɚɥɥɵ |
||||||||
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ, |
ɜɟɪɧɨɟ ɜɫɟ ɲɚɝɢ ɨɛɨɫɧɨɜɚɧɵ |
|
|
|
|
|
3 |
|||||
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ ɫɨɞɟɪɠɢɬ ɧɟɬɨɱɧɨɫɬɢ ɢɥɢ ɩɪɨɛɟɥɵ, ɧɚɩɪɢɦɟɪ, ɨɬɫɭɬɫɬɜɭɸɬ |
2 |
|||||||||||
ɫɫɵɥɤɢ ɧɚ ɫɜɨɣɫɬɜɚ ɩɚɪɚɥɥɟɥɶɧɵɯ ɩɪɹɦɵɯ ɢɥɢ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɚ |
|
|
||||||||||
|
|
|
||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɤɪɢɬɟɪɢɹɦ |
|
|
|
0 |
||||||||
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
3 |
|||
26 |
Ɉɫɧɨɜɚɧɢɟ AC ɪɚɜɧɨɛɟɞɪɟɧɧɨɝɨ |
ɬɪɟɭɝɨɥɶɧɢɤɚ |
ABC12. ɪɚɜɧɨ |
Ɉɤɪɭɠɧɨɫɬɶ |
||||||||
ɪɚɞɢɭɫɚ 8 ɫ ɰɟɧɬɪɨɦ ɜɧɟ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɤɚɫɚɟɬɫɹ ɩɪɨɞɨɥɠɟɧɢɹ ɛɨɤɨɜɵɯ ɫɬɨɪɨɧ ɬɪɟɭɝɨɥɶɧɢɤɚ ɢ ɤɚɫɚɟɬɫɹ ɨɫɧɨɜɚɧɢɹ AC ɜ ɟɝɨ ɫɟɪɟɞɢɧɟ. ɇɚɣɞɢɬɟ ɪɚɞɢɭɫ
ɨɤɪɭɠɧɨɫɬɢ, ɜɩɢɫɚɧɧɨɣ ɜ ɬɪɟɭɝɨɥɶɧɢɤ ABC.
Ɋɟɲɟɧɢɟ
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 5 |
4 |
Ⱦɚɧɧɚɹ ɨɤɪɭɠɧɨɫɬɶ ɤɚɫɚɟɬɫɹ ɫɬɨɪɨɧɵ AC ɜ ɟɺ ɫɟɪɟɞɢɧɟ M ɢ ɩɪɨɞɨɥɠɟɧɢɣ ɫɬɨɪɨɧ BA ɢ BC ɬɪɟɭɝɨɥɶɧɢɤɚ ABC
—ɉɭɫɬɶ O |
ɰɟɧɬɪ, |
ɷɬɨɣ ɨɤɪɭɠɧɨɫɬɢ |
ɚ Q—, |
|
ɰɟɧɬɪ ɨɤɪɭɠɧɨɫɬɢ |
ɜɩɢɫɚɧɧɨɣ ɜ |
|||||
ɬɪɟɭɝɨɥɶɧɢɤ ABC ɍɝɨɥ OAQ – ɩɪɹɦɨɣ ɤɚɤ ɭɝɨɥ ɦɟɠɞɭ ɛɢɫɫɟɤɬɪɢɫɚɦɢ ɫɦɟɠɧɵɯ ɭɝɥɨɜ. |
|||||||||||
Ɍɪɟɭɝɨɥɶɧɢɤ OAQ – ɩɪɹɦɨɭɝɨɥɶɧɵɣ, AM – ɟɝɨ ɜɵɫɨɬɚ. ɂɡ ɷɬɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɧɚɯɨɞɢɦ, |
|||||||||||
ɱɬɨ AM, 2 |
MQ MO. ɋɥɟɞɨɜɚɬɟɥɶɧɨ QM |
|
AM2 |
|
9 |
|
4,5. |
|
|
||
|
OM |
2 |
|
|
|
||||||
Ɉɬɜɟɬ 4, 5. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
Ʉɪɢɬɟɪɢɢ ɨ ɟɧɢɜɚɧɢɹ ɜɵɩɨɥɧɟɧɢɹ ɡɚɞɚɧɢɹ |
|
Ȼɚɥɥɵ |
|||||||
ɏɨɞ ɪɟɲɟɧɢɹ ɜɟɪɧɵɣ, ɜɫɟ ɟɝɨ ɲɚɝɢ ɜɵɩɨɥɧɟɧɵ ɩɪɚɜɢɥɶɧɨ, ɩɨɥɭɱɟɧ ɜɟɪɧɵɣ |
4 |
||||||||||
ɨɬɜɟɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɏɨɞ ɪɟɲɟɧɢɹ, |
ɜɟɪɧɵɣ ɜɫɟ ɟɝɨ ɲɚɝɢ |
ɜɵɩɨɥɧɟɧɵ |
ɩɪɚɜɢɥɶɧɨ, ɧɨ |
ɞɚɧɵ |
3 |
||||||
ɧɟɩɨɥɧɵɟ ɨɛɴɹɫɧɟɧɢɹ ɢɥɢ ɞɨɩɭɳɟɧɚ ɨɞɧɚ ɜɵɱɢɫɥɢɬɟɥɶɧɚɹ ɨɲɢɛɤɚ |
|
||||||||||
|
|
||||||||||
Ⱦɪɭɝɢɟ ɫɥɭɱɚɢ, ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɤɚɡɚɧɧɵɦ ɜɵɲɟ ɤɪɢɬɟɪɢɹɦ |
|
0 |
|||||||||
|
|
|
|
|
|
|
|
|
Ɇ ɤɫɢɦ ɥɶɧɵɣ ɛ ɥɥ |
4 |
|
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |
