1. Предматематическая подготовка, осуществляемая в детском саду, является частью общей подготовки детей к школе и заключается в формировании у них элементарных математических представлений. Этот процесс связан со всеми сторонами воспитательно-образовательной работы детского дошкольного учреждения и направлен прежде всего на решение задач умственного воспитания и математического развития дошкольников.

При постановке и реализации задач предматематической подготовки дошкольников учитывают: — закономерности становления и развития познавательной деятельности, умственных процессов и способностей, личности ребенка в целом; — возрастные возможности дошкольников в усвоении знаний и связанных с ними навыков и умений; — принцип преемственности в работе детского сада и школы.

Основные задачи предматематической подготовки детей в детском саду:

1. Формирование системы элементарных математических представлений у дошкольников. С содержательной стороны наиболее важными в смысле формирования первичных простейших представлений являются такие фундаментальные математические понятия, как «множество», «отношение», «число», «величина». Элементарные математические представления формируются н; базе освоения детьми в определенной последовательности способов действий (например, предлагается разложить столько предметов на свободной полоске, сколько их нарисовано на образце наложить полоски разной длины друг на друга, подобрать картинки с предметами к соответствующей геометрической фигуре и т. д.). Повышению уровня в обобщении математических представлений, формированию математических понятий способствует не только особая организация умственной деятельности, но и применение в процессе обучения специальных познавательных средств: моде лей, графиков, схем и т. д.

2. Формирование предпосылок математического мышления и отдельных логических структур, необходимых для овладения математикой в школе и общего умственного развития. Становление логических структур мышления — классификации, упорядочивания, понимание сохранения количества, массы объема и т. д. выступает как важная самостоятельная особенность общего умственного и математического развития ребенка-дошкольника.

3. Формирование сенсорных процессов и способностей. Основное направление в обучении маленьких детей — осуществление постепенного перехода от конкретных, эмпирических знаний к более обобщенным. Эмпирические знания, формируемые на основе сенсорного опыта,— предпосылка и необходимое условие умственного и математического развития детей дошкольного возраста.

Детей целенаправленно обучают отдельным приемам и обобщенным способам обследования: обведению контура предмета рукой и взглядом для выявления формы, «взвешиванию» предметов на ладонях обеих рук с целью сравнения их масс, наложению или приложению полосок бумаги для сравнения длины, сопоставлению элементов одной группы предметов с другой для выяснения отношений «больше», «меньше», «равно» и др.

4. Расширение словаря детей и совершенствование связной речи. Процесс формирования элементарных математических представлений предполагает планомерное усвоение и постепенное расширение словарного запаса, совершенствование грамматического строя и связности речи. Количественные отношения ребенок отражает с помощью слов много, один, ни одного, столько, сколько, поровну, больше, меньше и  т.   д.,   которые  осознаются   в  результате непосредственных действий при сравнении отдельных предметов и их совокупностей.

5. Формирование начальных форм учебной деятельности. Важную роль играет предматематическая подготовка и для становления начальных форм учебной деятельности. У детей вырабатываются   умения   слушать   и   слышать,   действовать   в соответствии с указаниями воспитателя, понимать и решать учебно-познавательные задачи определенными способами, использовать по назначению дидактический материал, выражать в словесной форме способы и результаты собственных действий и действий своих товарищей, контролировать и оценивать их, делать выводы и обобщения, доказывать их правильность и другие навыки и умения учебной деятельности. Задачи решаются не изолированно, а комплексно, в тесной связи друг с друго

2. Основные понятия теории множеств: виды, способы задания, пустое множество, графическая иллюстрация, подмножество.

Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.

Примеры множеств:

множество студентов в данной аудитории;

множество людей, живущих на нашей планете в данный момент времени;

множество точек данной геометрической фигуры;

множество чётных чисел;

множество корней уравнения х²-5х+6=0;

множество действительных корней уравнения х²+9=0;

Основоположник теории множеств немецкий математик Георг Кантор (1845-1918)

Объекты, составляющие данное множество, называют его элементами.

Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А, а если а не принадлежит А, то пишут: а А.

В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:

N- множество всех натуральных чисел;

Z- множество всех целых чисел;

Q- множество всех рациональных чисел;

R- множество всех действительных чисел.

Способы задания множества

Множество А считается заданным, если относительно любого объекта а можно установить, принадлежит этот объект множеству А или не принадлежит; другими словами, если можно определить, является ли а элементом множества А или не является. Существуют два основных способа задания множества:

перечисление элементов множества;

указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.

Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, … ,d ,обозначают с помощью фигурных скобок: А={a; b; c; …;d} . Множество корней уравнения х²-5х+6=0 состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2 < х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}.

Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р(х), также записывают с помощью фигурных скобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р(х). Например, А={х | х²-5х+6=0}. Решив уравнение х²-5х+6=0, мы можем записать множество А первым способом: А={2; 3}.

Множества, которые состоят из определённого конечного числа предметов называют конечными.

Множество точек отрезка пересчитать невозможно, поэтому такие множества называются бесконечными.

Множество, не содержащее ни одного элемента, называется пустым множеством.

Если каждый элемент множества В является также элементом множества А, множество В называется подмножеством множества А (обозначение - B A или A B).

Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B.

3. Основные операции над множествами: объединение

Объединением АВ множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.

Символическая запись этого определения: А В={х | хА или хВ}.

Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз).

Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:

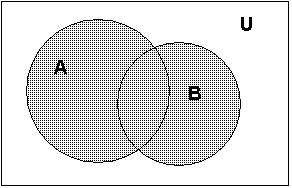
На диаграмме объединение множеств А и В выделено штриховкой.

Примеры объединений двух множеств:

1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А В ={2; 3; 5; 6; 7}.

2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А В=[-2/3; 2] .

Объединение обладает свойствами:

1) коммуникативности, т.е. АВ=ВА,

2) ассоциативности, т.е. А(ВС)=(АВ) С

3) дистрибутивности относительно пересечения, т.е. А(ВС)=(АВ) ∩(АС)

А∩Ø= Ø

А Ø=А

А∩А=А

АА=А

Совокупность всех множеств называется универсальным множеством (V,U,Y)

А∩V=А

АV= V

Любое множество является подмножеством универсального множества.

Если множество А конечно, то можно найти число его подмножеств.

Если множество А содержит подмножество с, то число подмножеств равно 2^с

(n(A)=c,2^c)

А={а, в, с}

N(A)=3

2³=8

А₁={а}

А₂={в}

А₃={с}

А₄={а,в}

А₅={а,с}

А₆={в,с}

А₇={а,в,с}

А₈= Ø

4.Основные операции над множествами: разность множеств

Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.

А\В={х | х А и хВ}, что можно пояснить на диаграмме Эйлера-Венна следующим образом:

На диаграмме разность А\В выделена штриховкой.

Примеры разностей множеств:

Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.

Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4).

Если множество А является подмножеством множества В, то разность называют дополнением множества А до множества В.

АС

В\А=À_в=Ᾱ_в

A-множество натуральных чисел кратных 5

В – множество натуральных чисел

À_в – множество натуральных чисел не кратных 5

6.Развитие понятия натурального числа и счетной деятельности

К построению математических моделей явлений, основанному на отвлечении от всех свойств предметов, кроме их количественных отношений и пространственных форм, человечество прибегало с первых шагов изучения окружающего мира. Одним из первых достижений на этом пути было возникновение и формирование понятия натурального числа. Оно появилось, по-видимому, на довольно позднем этапе развития мышления, поскольку предполагает уже способность к созданию и оперированию абстрактными понятиями.

В процессе практической деятельности люди пришли к абстрагированию такого общего свойства конечных множеств, каким является их численность. Чтобы усмотреть нечто общее между множеством, состоящим из шести рыб, и множеством, состоящим из шести звезд, нужна уже высокая степень умения абстрагироваться от второстепенного, умение выделять главное. Этнографы нашли племена, в языках которых существует много видов числительных: числительные для множеств живых существ отличаются от числительных для множеств плодов, орудий охоты и т. д. Однако на ранней стадии развития люди еще не могли достигать в рассуждениях достаточной степени общности и уровень абстрагирования еще не позволял формулировать общие свойства предметов, каким является натуральное число, и тем более вводить для его обозначения специальные символы.

Процесс формирования понятия числа был сложным и длительным. На самом раннем этапе устанавливалась равночисленность различных множеств, общее же свойство равночисленных множеств еще не отделялось от конкретной природы сравниваемых множеств. Например, знали, что два рыболова поймали поровну рыб, но не выражали этого каким-либо числом. В дальнейшем практика экономических и социальных взаимоотношений привела к необходимости выражать численность одних множеств уже через численность других множеств, т. е. общее свойство равночисленности стало осознаваться как нечто отличное от конкретной природы самого множества, его элементов. Однако в качестве эталонов выступают еще различные множества, состоящие из подручных предметов - эквивалентов равночисленности множеств предметов.