
- •Учебно-методическое пособие для подготовки к интернет-экзамену по математике для студентов технических специальностей спо
- •Раздел 1 элементы линейной алгебры
- •Тема 1 матрицы. Действия над матрицами. Умножение матриц
- •1.2Действия над матрицами
- •Тема 2 определители. Вычисление определителей второго и третьего порядков
- •Тема 3 системы линейных уравнений. Правила крамера. Метод гаусса конспект 3
- •3.1 Правило крамера
- •Раздел 2 элементы аналитической геометрии
- •Тема 4 координаты точек на плоскости и в пространстве
- •Тема 5 линейные операции над векторами. Скалярное произведение векторов
- •5.2 Простейшие задачи в координатах
- •5.4 Скалярное произведение векторов
- •Понятие скалярного произведения
- •Скалярное произведение в координатах
- •Проверка векторов на ортогональность с помощью скалярного произведения
- •Тема 6 линии и их уравнения на плоскости. Уравнение прямой на плоскости
- •6.1 Уравнение прямой на плоскости
- •6.1.1 Уравнение прямой с угловым коэффициентом
- •6.1.2 Общее уравнение прямой на плоскости
- •6.1.3 Каноническое уравнение
- •6.1.4 Уравнение прямой, проходящей через две данные точки.
- •Тема 7 кривые второго порядка
- •Кривая второго порядка может быть задана уравнением
- •Раздел 3
- •Тема 8. Правила дифференцирования Производная сложной функции. Производная функции в точке. Конспект 8
- •8.1 Правила дииференцирования
- •Тема 9 экстремум функции. Наибольшее и наименьшее значения функции
- •9.1 Порядок нахождения экстремумов функции
- •Тема 10 дифференциал функции
- •10.1 Дифференциал функции одной переменной
- •Раздел 4
- •Тема 11 неопределенный интеграл. Методы вычисления неопределенного интеграла конспект 11
- •1.1 Неопределенный интеграл
- •Метод замены переменной в неопределенном интеграле
- •Тема 12 опреленный интеграл. Формула ньютона-лейбница. Свойства определенного интеграла
- •Тема 13 геометрические приложения определенного интеграла. Физические приложения определенного интеграла
- •13.1 Геометрические приложения интеграла
- •Раздел 5.
- •Тема 14 элементы комбинаторики. Классическое определение вероятности. Математическое ожидание дискретной случайной величины
- •Тема 15 характеристики вариационного ряда. Выборочное среднее. Объем выборки
- •Раздел 6.
- •Тема 16 действия над комплексными числами в алгебраической форме. Решение квадратных уравнений
- •Тема 17 сопряженные комплексные числа. Модуль комплексного числа
- •Тема 18 тригонометрическая форма комплексного числа. Действия над комплексными числами в тригонометрической форме конспект 18.
- •18.1 Тригонометрическая форма комплексного числа
- •Раздел 7.
- •Тема 19 способы задания числовых последовательностей. Предел функции в точке
- •Тема 20 раскрытие неопределенности вида «ноль на ноль». Раскрытие неопределенности «бесконечность на бесконечность»
- •Тема 21 первый замечательный предел. Второй замечательный предел
Метод замены переменной в неопределенном интеграле
Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле.
Пример 2
Найти
неопределенный интеграл.
![]()
Идея
метода замены состоит в том, чтобы
сложное выражение (или некоторую
функцию) заменить одной буквой.В
данном случае напрашивается:![]() Вторая
по популярности буква для замены – это
буква
Вторая
по популярности буква для замены – это
буква![]() .
В
принципе, можно использовать и другие
буквы, но мы всё-таки будем придерживаться
традиций.
.
В
принципе, можно использовать и другие
буквы, но мы всё-таки будем придерживаться
традиций.
Итак:
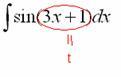 Но
при замене у нас остаётся
Но
при замене у нас остаётся![]() !
Наверное, многие догадались, что если
осуществляется переход к новой переменной
!
Наверное, многие догадались, что если
осуществляется переход к новой переменной![]() ,
то в новом интеграле всё должно быть
выражено через букву
,
то в новом интеграле всё должно быть
выражено через букву![]() ,
и дифференциалу
,
и дифференциалу![]() там
совсем не место.
Следует логичный
вывод, что
там
совсем не место.
Следует логичный
вывод, что![]() нужнопревратить в некоторое выражение,
которое зависит только от
нужнопревратить в некоторое выражение,
которое зависит только от
![]() .
.
Действие
следующее. После того, как мы подобрали
замену, в данном примере,
![]() ,
нам нужно найти дифференциал
,
нам нужно найти дифференциал![]() .
Так как
.
Так как![]() ,
то
,
то
![]()
После
разборок с дифференциалом окончательный
результат рекомендую переписать
максимально коротко:
![]() Теперь
по правилам пропорции выражаем нужный
нам
Теперь
по правилам пропорции выражаем нужный
нам![]() :
:![]()
В
итоге:
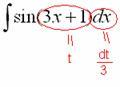 Таким
образом:
Таким
образом:![]() А
это уже самый что ни на есть табличный
интеграл
А
это уже самый что ни на есть табличный
интеграл![]() (таблица,
интегралов, естественно, справедлива
и для переменной
(таблица,
интегралов, естественно, справедлива
и для переменной![]() ).
).
![]() В
заключении осталось провести обратную
замену. Вспоминаем, что
В
заключении осталось провести обратную
замену. Вспоминаем, что![]() .
.
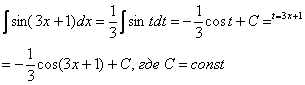 Готово.
Готово.
11.3 ТАБЛИЦА ИНТЕГРАЛОВ
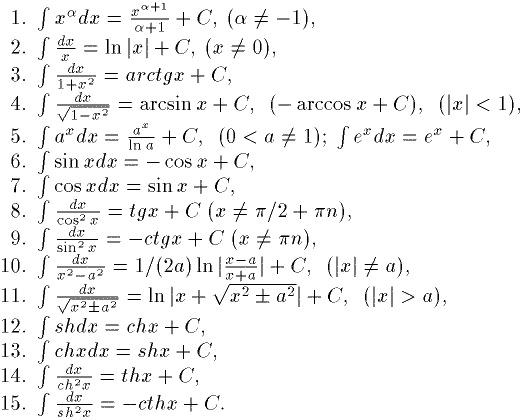
ПРАКТИКУМ 11
ЗАДАНИЕ N 1Тема:
Неопределенный интегралНеопределенный
интеграл![]() равен …
равен …
Решение:Напоминаем, что интеграл
суммы двух функций равен сумме интегралов
этих функций![]() и
постоянный множитель можно выносить
за знак неопределенного интеграла:
и
постоянный множитель можно выносить
за знак неопределенного интеграла:![]() Тогда,
используя формулу
Тогда,
используя формулу ,
получим:
,
получим: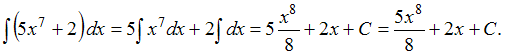
ЗАДАНИЕ N 2Тема:
Методы вычисления неопределенных
интегралов![]() …
…
Решение:Подстановка![]() приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному: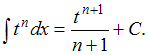 Найдем
дифференциал от обеих частей подстановки:
Найдем
дифференциал от обеих частей подстановки:![]() ,
тогда
,
тогда![]() Подставим
получившиеся выражения в исходный
интеграл:
Подставим
получившиеся выражения в исходный
интеграл: Заменив
Заменив![]() его
выражением из подстановки, получим:
его
выражением из подстановки, получим: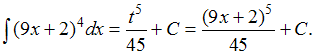
ЗАДАНИЕ N 3Тема:
Неопределенный интеграл![]() …
…
Решение:Напоминаем, что интеграл
разности двух функций равен разности
интегралов этих функций![]() и
постоянный множитель можно выносить
за знак неопределенного интеграла:
и
постоянный множитель можно выносить
за знак неопределенного интеграла:![]() Тогда,
используя формулу
Тогда,
используя формулу![]() ,
получим:
,
получим:![]()
ЗАДАНИЕ N 4Тема:
Методы вычисления неопределенных
интегралов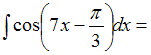 …
…
Решение:Подстановка![]() приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному:![]() Найдем
дифференциал от обеих частей подстановки:
Найдем
дифференциал от обеих частей подстановки:![]() ,
тогда
,
тогда![]() Подставим
получившиеся выражения в исходный
интеграл:
Подставим
получившиеся выражения в исходный
интеграл: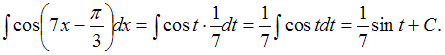 Заменив
Заменив![]() его
выражением из подстановки, получим:
его
выражением из подстановки, получим: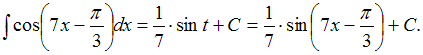
ЗАДАНИЕ N 5Тема:
Неопределенный интегралНеопределенный
интеграл![]() равен …
равен …
Решение:Напоминаем, что постоянный
множитель можно выносить за знак
неопределенного интеграла:![]() Тогда,
используя формулу
Тогда,
используя формулу![]() ,
получим:
,
получим:![]()
ЗАДАНИЕ N 6Тема:
Методы вычисления неопределенных
интегралов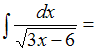 …
…
Решение:Подстановка![]() приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному: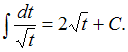 Найдем
дифференциал от обеих частей подстановки:
Найдем
дифференциал от обеих частей подстановки:![]() ,
тогда
,
тогда![]() Подставим
получившиеся выражения в исходный
интеграл:
Подставим
получившиеся выражения в исходный
интеграл: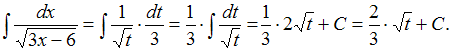 Заменив
Заменив![]() его
выражением из подстановки, получим:
его
выражением из подстановки, получим: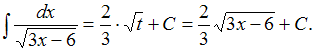
ЗАДАНИЕ N 7Тема:
Методы вычисления неопределенных
интегралов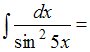 …
…
Решение:Подстановка![]() приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному: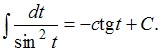 Найдем
дифференциал от обеих частей подстановки:
Найдем
дифференциал от обеих частей подстановки:![]() ,
тогда
,
тогда![]() Подставим
получившиеся выражения в исходный
интеграл:
Подставим
получившиеся выражения в исходный
интеграл: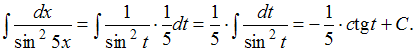 Заменив
Заменив![]() его
выражением из подстановки, получим:
его
выражением из подстановки, получим: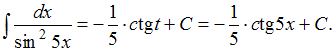
ЗАДАНИЕ N 8Тема:
Неопределенный интеграл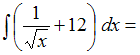 …
…
Решение:Напоминаем, что интеграл
суммы двух функций равен сумме интегралов
этих функций![]() и
постоянный множитель можно выносить
за знак неопределенного интеграла:
и
постоянный множитель можно выносить
за знак неопределенного интеграла:![]() Тогда,
используя формулу
Тогда,
используя формулу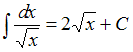 ,
получим:
,
получим: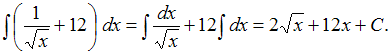
ЗАДАНИЕ N 9Тема:
Методы вычисления неопределенных
интеграловНеопределенный интеграл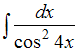 равен …
равен …
Решение:Обращаем внимание, что
подстановка![]() приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному: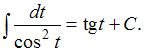 Найдем
дифференциал от обеих частей подстановки:
Найдем
дифференциал от обеих частей подстановки:![]() ,
тогда
,
тогда![]() Подставим
получившиеся выражения в исходный
интеграл:
Подставим
получившиеся выражения в исходный
интеграл:![]() Заменив
Заменив![]() его
выражением из подстановки, получим:
его
выражением из подстановки, получим:![]()
ЗАДАНИЕ N 10Тема:
Методы вычисления неопределенных
интегралов![]() …
…
Решение:Подстановка![]() приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному:![]() Найдем
дифференциал от обеих частей подстановки:
Найдем
дифференциал от обеих частей подстановки:![]() ,
тогда
,
тогда![]() Подставим
получившиеся выражения в исходный
интеграл:
Подставим
получившиеся выражения в исходный
интеграл:![]() Заменив
Заменив![]() его
выражением из подстановки, получим:
его
выражением из подстановки, получим:![]()
САМОСТОЯТЕЛЬНАЯ РАБОТА 11
ЗАДАНИЕ N 1Тема:
Неопределенный интеграл![]() …
…
ЗАДАНИЕ N 2Тема:
Неопределенный интеграл![]() …
…
ЗАДАНИЕ N 3Тема:
Методы вычисления неопределенных
интегралов![]() …
…
ЗАДАНИЕ N 4Тема:
Неопределенный интеграл![]() …
…
ЗАДАНИЕ N 5Тема:
Методы вычисления неопределенных
интеграловНеопределенный
интеграл
![]() равен …
равен …
ЗАДАНИЕ N 6Тема:
Неопределенный интеграл![]() …
…
ЗАДАНИЕ N 7Тема:
Методы вычисления неопределенных
интегралов![]() …
…
ЗАДАНИЕ N 8Тема:
Неопределенный интегралНеопределенный
интеграл
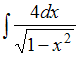 равен …ЗАДАНИЕ
N 9 Тема: Неопределенный интеграл
равен …ЗАДАНИЕ
N 9 Тема: Неопределенный интеграл![]()
ЗАДАНИЕ N 10 Тема:
Неопределенный интеграл![]() …
…
