
- •Учебно-методическое пособие для подготовки к интернет-экзамену по математике для студентов технических специальностей спо
- •Раздел 1 элементы линейной алгебры
- •Тема 1 матрицы. Действия над матрицами. Умножение матриц
- •1.2Действия над матрицами
- •Тема 2 определители. Вычисление определителей второго и третьего порядков
- •Тема 3 системы линейных уравнений. Правила крамера. Метод гаусса конспект 3
- •3.1 Правило крамера
- •Раздел 2 элементы аналитической геометрии
- •Тема 4 координаты точек на плоскости и в пространстве
- •Тема 5 линейные операции над векторами. Скалярное произведение векторов
- •5.2 Простейшие задачи в координатах
- •5.4 Скалярное произведение векторов
- •Понятие скалярного произведения
- •Скалярное произведение в координатах
- •Проверка векторов на ортогональность с помощью скалярного произведения
- •Тема 6 линии и их уравнения на плоскости. Уравнение прямой на плоскости
- •6.1 Уравнение прямой на плоскости
- •6.1.1 Уравнение прямой с угловым коэффициентом
- •6.1.2 Общее уравнение прямой на плоскости
- •6.1.3 Каноническое уравнение
- •6.1.4 Уравнение прямой, проходящей через две данные точки.
- •Тема 7 кривые второго порядка
- •Кривая второго порядка может быть задана уравнением
- •Раздел 3
- •Тема 8. Правила дифференцирования Производная сложной функции. Производная функции в точке. Конспект 8
- •8.1 Правила дииференцирования
- •Тема 9 экстремум функции. Наибольшее и наименьшее значения функции
- •9.1 Порядок нахождения экстремумов функции
- •Тема 10 дифференциал функции
- •10.1 Дифференциал функции одной переменной
- •Раздел 4
- •Тема 11 неопределенный интеграл. Методы вычисления неопределенного интеграла конспект 11
- •1.1 Неопределенный интеграл
- •Метод замены переменной в неопределенном интеграле
- •Тема 12 опреленный интеграл. Формула ньютона-лейбница. Свойства определенного интеграла
- •Тема 13 геометрические приложения определенного интеграла. Физические приложения определенного интеграла
- •13.1 Геометрические приложения интеграла
- •Раздел 5.
- •Тема 14 элементы комбинаторики. Классическое определение вероятности. Математическое ожидание дискретной случайной величины
- •Тема 15 характеристики вариационного ряда. Выборочное среднее. Объем выборки
- •Раздел 6.
- •Тема 16 действия над комплексными числами в алгебраической форме. Решение квадратных уравнений
- •Тема 17 сопряженные комплексные числа. Модуль комплексного числа
- •Тема 18 тригонометрическая форма комплексного числа. Действия над комплексными числами в тригонометрической форме конспект 18.
- •18.1 Тригонометрическая форма комплексного числа
- •Раздел 7.
- •Тема 19 способы задания числовых последовательностей. Предел функции в точке
- •Тема 20 раскрытие неопределенности вида «ноль на ноль». Раскрытие неопределенности «бесконечность на бесконечность»
- •Тема 21 первый замечательный предел. Второй замечательный предел
Тема 10 дифференциал функции
КОНСПЕКТ 10
10.1 Дифференциал функции одной переменной
В самой примитивной формулировке дифференциал – это «почти то же самое, что и производная».
Производная
функции чаще всего обозначается через
![]() .
.
Дифференциал
функции стандартно обозначается через
![]() (так
и читается – «дэ игрек»)
(так
и читается – «дэ игрек»)
Дифференциал функции одной переменной записывается в следующем виде:
![]()
Другой
вариант записи:
![]()
Простейшая
задача: Найти дифференциал функции
![]()
1) Первый этап. Найдем производную:
![]()
2) Второй этап. Запишем дифференциал:
![]() Готово.
Готово.
Дифференциал функции одной или нескольких переменных чаще всего используют для приближенных вычислений.
Для приближенного вычисления значения
функции y(x) в точке
![]() можно
использовать формулу:
можно
использовать формулу:![]() где
где![]() приращение
функции в точке
приращение
функции в точке![]() Функция
y(x) определяется из условия задачи
Значения
Функция
y(x) определяется из условия задачи
Значения![]() и
и![]() выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить![]() и
при этом
и
при этом![]() ,
взятое по модулю, было бы как можно
меньше.
,
взятое по модулю, было бы как можно
меньше.
10.2 ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
Для того, чтобы получить простейшую приближенную формулу для производной, нужно знать только ее определение:
![]() . (3.1)
. (3.1)
При малом hможно положить:
![]() . (3.2)
. (3.2)
Это и есть простейшая приближенная формула.
В определении (3.1) hможет принимать значения обоих знаков. В дискретной записи принято обозначать черезhположительное число, так что можно написать еще одну формулу:
![]() (3.2´)
(3.2´)
Какую ошибку мы совершаем, заменяя производную разностным отношением по формуле (3.2)? Это легко сообразить. Напишем:
![]()
![]() .
.
Отсюда
![]() ,
,
где m2=min|![]() |,M2=max|
|,M2=max|![]() |.
При
|.
При![]() ошибка
стремится к нулю со скоростьюhили,
как говорят, формула (3.2) имеет первый
порядок точности. Сложением формул
(3.2) и (3.2') получается симметричная
формула:
ошибка
стремится к нулю со скоростьюhили,
как говорят, формула (3.2) имеет первый
порядок точности. Сложением формул
(3.2) и (3.2') получается симметричная
формула:
![]() . (3.3)
. (3.3)
Формула (3.3), как легко проверить, точнее
формулы (3.2), а именно, ошибка здесь имеет
порядок
![]() — это есть формула второго порядка
точности потому, что ошибка не превосходит
— это есть формула второго порядка
точности потому, что ошибка не превосходит![]() ,
гдеM3=max|
,
гдеM3=max|![]() |.
Это увеличение точности получилось
только за счет симметрии. Это случается
очень часто.
|.
Это увеличение точности получилось
только за счет симметрии. Это случается
очень часто.
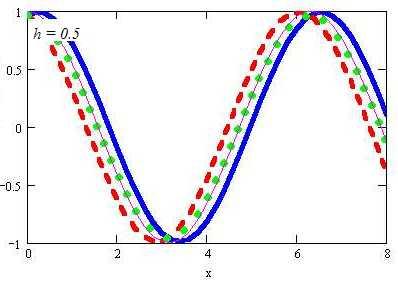
Рис. 1.
На рисунке 1 приведены результаты вычисления производной функции f(x) = sin(x) по трем разностным формулам (3.2, 3.2´ и 3.3) вместе с точным графиком производной.
ПРАКТИКУМ 10
ЗАДАНИЕ N 1Тема:
Дифференциал функцииДля приближенного
вычисления значения функцииy(x)
в точке![]() можно
использовать формулу
можно
использовать формулу![]() где
где![]() приращение
функции в точке
приращение
функции в точке![]() Функцияy(x) определяется из условия
задачи.
Значения
Функцияy(x) определяется из условия
задачи.
Значения![]() и
и![]() выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить![]() и
при этом
и
при этом![]() ,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения![]() равно …
равно …
Решение:![]() .
.![]() Так
как
Так
как![]() ,
то можно рассмотреть функцию
,
то можно рассмотреть функцию![]() Пусть
Пусть![]() тогда
тогда![]() Имеем:
Имеем: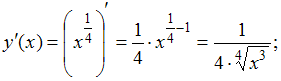
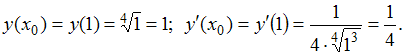 По
формуле
По
формуле![]() получим
получим![]()
ЗАДАНИЕ N 2Тема:
Дифференциал функцииДля приближенного
вычисления значения функцииy(x)в
точке![]() можно
использовать формулу:
можно
использовать формулу:![]() где
где![]() приращение
функции в точке
приращение
функции в точке![]() Функцияy(x)определяется из условия задачи
Значения
Функцияy(x)определяется из условия задачи
Значения![]() и
и![]() выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить![]() и
при этом
и
при этом![]() ,
взятое по модулю, было бы как можно
меньше.
Тогда наилучшее приближенное
значение выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда наилучшее приближенное
значение выражения![]() равно …
равно …
Решение:![]() .
.![]() Так
как
Так
как![]() ,
то можно рассмотреть функцию
,
то можно рассмотреть функцию![]() Для
Для![]() имеем:
имеем:![]() Тогда
Тогда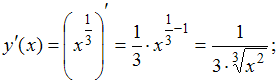
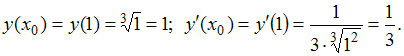 По
формуле
По
формуле![]() получим
получим![]()
ЗАДАНИЕ N 3Тема:
Дифференциал функцииДля приближенного
вычисления значения функцииy(x)в
точке![]() можно
использовать формулу:
можно
использовать формулу:![]() где
где![]() приращение
функции в точке
приращение
функции в точке![]() Функцияy(x)определяется из условия задачи.
Значения
Функцияy(x)определяется из условия задачи.
Значения![]() и
и![]() выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить![]() и
при этом
и
при этом![]() ,
взятое по модулю, было бы как можно
меньше.
Тогда наилучшее приближенное
значение выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда наилучшее приближенное
значение выражения![]() равно …
равно …
Решение:![]() .
Так как
.
Так как![]() ,
то можно рассмотреть функцию
,
то можно рассмотреть функцию![]() Для
Для![]() имеем:
имеем:![]() Тогда
Тогда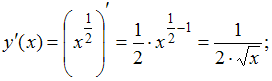
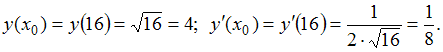 По
формуле
По
формуле![]() получим:
получим:![]()
САМОСТОЯТЕЛЬНАЯ РАБОТА 10
ЗАДАНИЕ N 1Тема:
Дифференциал функцииДля приближенного
вычисления значения функцииy(x)в
точке![]() можно
использовать формулу:
можно
использовать формулу:![]() где
где![]() приращение
функции в точке
приращение
функции в точке![]() Функцияy(x)определяется из условия задачи.
Значения
Функцияy(x)определяется из условия задачи.
Значения![]() и
и![]() выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить![]() и
при этом
и
при этом![]() ,
взятое по модулю, было бы как можно
меньше.
Тогда наилучшее приближенное
значение выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда наилучшее приближенное
значение выражения![]() равно …
равно …
ЗАДАНИЕ N 2Тема:
Дифференциал функцииДля приближенного
вычисления значения функцииy(x)в
точке![]() можно
использовать формулу:
можно
использовать формулу:![]() где
где![]() приращение
функции в точке
приращение
функции в точке![]() Функцияy(x)определяется из условия задачи.
Значения
Функцияy(x)определяется из условия задачи.
Значения![]() и
и![]() выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить![]() и
при этом
и
при этом![]() ,
взятое по модулю, было бы как можно
меньше.
Тогда наилучшее приближенное
значение выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда наилучшее приближенное
значение выражения![]() равно …
равно …
ЗАДАНИЕ N 3Тема:
Дифференциал функцииДля приближенного
вычисления значения функцииy(x)
в точке![]() можно
использовать формулу
можно
использовать формулу![]() где
где![]() приращение
функции в точке
приращение
функции в точке![]() Функцияy(x) определяется из условия
задачи.
Значения
Функцияy(x) определяется из условия
задачи.
Значения![]() и
и![]() выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить![]() и
при этом
и
при этом![]() ,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения![]() равно …
равно …
ЗАДАНИЕ N 4Тема:
Дифференциал функцииДля приближенного
вычисления значения функцииy(x)
в точке![]() можно
использовать формулу
можно
использовать формулу![]() где
где![]() приращение
функции в точке
приращение
функции в точке![]() Функцияy(x) определяется из условия
задачи.
Значения
Функцияy(x) определяется из условия
задачи.
Значения![]() и
и![]() выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить![]() и
при этом
и
при этом![]() ,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения![]() равно …
равно …
