
- •1. Основные цели и задачи физического практикума. Общие требования к выполнению лабораторных работ по физике
- •2. Общие сведения о физических измерениях
- •3. Классификация погрешностей измерений
- •Погрешности
- •4. Теория случайных погрешностей
- •5. Правила обработки результатов измерений
- •6. Графические методы обработки результатов измерений в физическом эксперименте
- •2 Стр.Отчета
5. Правила обработки результатов измерений
5.1. Правила округления окончательного результата и абсолютной погрешности. При оформлении окончательного ответа следует придерживаться следующих правил.
1. Абсолютная погрешность показывает, в каком разряде числа содержится неточность (сомнительная цифра). Поэтому абсолютную погрешность округляют ДО ПЕРВОЙ ЗНАЧАЩЕЙ ЦИФРЫ (всегда с избытком).
Если абсолютная погрешность содержит первую значащую цифру «1», а следующая меньше «5», то ее можно округлять до двух значащих цифр (с избытком).
2. В окончательно результате оставляют ВСЕ ВЕРНЫЕ цифры и ОДНУ СОМНИТЕЛЬНУЮ, т.е. окончательный результат округляют по правилам действия с приближенными числами (прилож.2) до того разряда, на который указывает абсолютная погрешность.
Например, при измерениях времени падения шарика с заданной высоты получили следующие результаты:
<> = 0,414 с; = 0,018 с.
Округляем абсолютную погрешность до первой значащей цифры (до разряда сотых долей) с избытком: 0,02 с. Тогда среднее значение времени <> следует округлить также с точностью до сотых (по правилам округления приближенных чисел): <> 0,41 с.
Ответ должен быть записан в виде: = (0,410,02) с. Далее рассчитываем относительную погрешность: =(0,02/0,41)100%=5%. Так как < 10% (10% - это предельно допустимая погрешность), то делаем вывод о том, что полученные результаты получены достаточно точные.
Когда эксперимент проведен недостаточно добросовестно, относительная ошибка получается больше 10%. В этом случае рекомендуется проверить свой эксперимент, проведя более тщательно измерения, либо выявить причину большой погрешности и объяснить ее существование.
Точность округления результатов должна согласовываться с точностью самих измерений. Если, например, штангенциркуль, с помощью которого измеряли толщину бруска, имеет цену деления
0,1 мм, то нет смысла рассчитывать среднее значение измеряемой величины до тысячных и тем более, до десятитысячных. Большое число десятичных знаков в числе приводит к большому объему ненужной работы.
Рис.6
Наконец, укажем физический смысл записи результата в виде: Х = <X> X
(с надежностью ).
Такая запись результата означает, что истинное значение измеряемой величины лежит в доверительном интервале с надежностью , т.е. истинное значение а [<X>-Х, <X>+Х] (рис.6). Чтобы истинное значение “не выпало” за пределы доверительного интервала, абсолютную погрешность Х рекомендуется округлять всегда с избытком.
Кроме того, предложенная форма записи окончательного результата позволяет судить о том, в каком разряде содержится неточность (сомнительная цифра), а какие цифры являются верными.
5.2. Правила обработки прямых измерений. При выполнении лабораторного практикума студент должен не только произвести необходимые измерения, но он должен также уметь их анализировать. При этом он должен придерживаться определенных правил. Правила обработки прямых измерений приведены ниже (табл.5).
Таблица 5
округлив X согласно правилам округления абсолютной ошибки (§5.1) и <X> в соответствии с правилами округления приближенных чисел (см. прилож.2).
|
5.3. Абсолютная погрешность физических постоянных. Очень часто формулы, связывающие исследуемую величину с измеряемыми, содержат физические постоянные, как число «», ускорение свободного падения «g», постоянную Больцмана «k», универсальную газовую постоянную «R» и т.д. Возникает вопрос, как оценивать абсолютную погрешность таких величин. Существует правило: за абсолютную погрешность физических констант принимается половина последнего разряда в числе.
Например, = 3,14; следовательно, последний разряд в числе сотые доли; поэтому 0,01/2 = 0,005, т.е. =0,005.
Другой пример. Ускорение свободного падения g=9,81 м/с2. Тогда g=0,005 м/с2; если значение g=9,8 м/с2, то g=0,05 м/с2; если же g=10 м/с2, то g=0,5 м/с2.
5.4. Правила обработки косвенных измерений. В случае косвенных измерений обработку результатов эксперимента можно производить двумя способами. Если исследуемая величина определяется несколько раз при НЕИЗМЕННЫХ внешних условиях, то расчет погрешностей можно производить выше описанным методом (как для прямых измерений).
Например,
при определении ускорения свободного
падения методом математического маятника
ЗАДАННОЙ длины измеряют время ОДИНАКОВОГО
числа колебаний (![]() =const,
n=const),
находят период Ti
для каждого опыта (Ti
=
ti/n)
и рассчитываю ускорение свободного
падения по формуле:
=const,
n=const),
находят период Ti
для каждого опыта (Ti
=
ti/n)
и рассчитываю ускорение свободного
падения по формуле:
![]()
Затем рассчитывают среднее значение <g> и дальше обработку результатов проводят согласно приведенным правилам (см. табл. 5).
Если же внешние условия меняются в ходе эксперимента и исследуемая величина находится в некоторой зависимости от этих условий, то обработку результатов следует проводить другим методом, основанным на правилах дифференцирования с учетом погрешностей прямых измерений.
Например, при определении коэффициента вязкости жидкости при различных температурах, можно установить зависимость этого коэффициента от t0C, но невозможно определить его среднее значение. Поэтому расчет погрешности будет отличным по сравнению с прямыми измерениями.
Итак, пусть исследуемая величина является функцией нескольких переменных: y = f(x1, x2, …, xn). Продифференцировав данную функцию по каждой переменной (в частных производных), получим формулу относительной погрешности i = уi/yi, а затем, зная i и уi, рассчитываем абсолютную погрешность: уi = i/yi. Эти расчеты обычно проводят для каждого опыта, а затем находят среднюю абсолютную погрешность по формуле (5).
На практике часто применяют другой способ вывода формулы относительной погрешности, алгоритм нахождения которой приведен ниже (табл.6)
Таблица 6
ln y = ln[f(x1, x2, …, xn)]
где i = 1, 2, 3, … - номер опыта. Значения x1, x2, …, xn, входящие в формулу (14), есть абсолютные погрешности прямых измерений, определяемые выше описанным способом (см. табл. 5). Выражение (14) есть выражение максимальной относительной погрешности.
|
5.5.
Пример
обработки косвенных измерений.
Рассмотрим пример обработки косвенных
измерений периода колебаний математического
маятника: а) при неизменных внешних
условиях (![]() =const,
n=const);
б) при изменении внешних условий (
=const,
n=const);
б) при изменении внешних условий (![]() иn
будут меняться из опыта в опыт).
иn
будут меняться из опыта в опыт).
Экспериментальные данные соответственно приведены в табл.7 и табл.8
Таблица 7
|
№ п/п |
|
n, колеб. |
, с |
Т, с |
|Тi|, с |
(Тi)2, с2 | |
|
1 2 3 |
1,0 |
10 |
20,16 20,13 20,14 |
2,016 2,013 2,014 |
1,710-3 1,310-3 0,310-3 |
2,8910-6 1,6910-6 0,0910-6 | |
|
Среднее значение |
20,143 |
2,0143 |
| ||||
Определив абсолютные погрешности каждого опыта и их квадраты, оценим случайную погрешность по формуле Стьюдента (13).
 ,
,
где t,n = 4,31 для n = 3 и = 0,95 (табл.4)
Подставим значения |Т| и (Т)2 из табл.7 в последнюю формулу.
![]()
= 4,310,88210-3 = 3,810-3 0,0038 (с).
Полученное число округляем до первой значащей цифры (разряд тысячных): Т = 0,004 (с). Среднее значение периода округляем до разряда тысячных и окончательный результат представляем в виде:
Т = (2,014 0,004) с (с надежностью =0,95).
Относительная погрешность равна

Относительную погрешность обычно округляют до двух-трех значащих цифр.
Таким образом, получили 0,20%, что меньше 1%. Такая незначительная погрешность указывает на то, что получены удовлетворительные результаты.
Рассмотрим теперь пример обработки результатов косвенных измерений периода колебаний математического маятника, когда внешние условия изменяются (из опыта в опыт меняется длина маятника). Результаты такого эксперимента представлены в табл.8.
Таблица 8
|
№ п/п |
n, колеб. |
|
, с |
Т, с |
|
Т, с |
|
1 2 3 |
10 |
0,6 0,8 1,0 |
1,553 17,93 20,05 |
1,553 1,793 2,005 |
0,026 0,026 0,026 |
0,05 0,05 0,06 |
|
Среднее значение |
0,06 | |||||
В данном случае, среднее значение периода находить нельзя, т.к. в каждом опыте он был найден при различных условиях (менялась длина маятника).
Поэтому при обработке результатов измерений воспользуемся алгоритмом, представленным табл.6. Для этого запишем формулу периода колебаний:
![]() (15)
(15)
Следуя правилам (табл.6), проделаем следующие операции:
1) прологарифмируем выражение (15):
ln
T
= ln
2 + ln
+ ½(ln
![]() - ln
g);
- ln
g);
2) продифференцируем последнее соотношение, заменяя значок дифференциала «d» на «» и знак «минус» на «плюс»:
![]()
3) каждое слагаемое возведем в квадрат и извлечем из обеих частей квадратный корень:
![]()
где
= 0,005 (§5.3); g
= 0,05 м/с2;
![]() =0,5
см (половина цены деления линейки).
=0,5
см (половина цены деления линейки).
Рассчитаем относительную погрешность для каждого опыта (табл.8):



Сравнивая 1, 2 и 3, видим, что относительная погрешность получается одинаковая. Поэтому достаточно рассчитать для одного опыта (обычно для средней части таблицы).
Найдем абсолютные погрешности всех измерений:
Т1 = Т1 = 0,0261,553 = 0,0404 0,05 (с)
Т2 = Т2 = 0,0261,793 = 0,0466 0,05 (с)
Т3 = Т3 = 0,0262,005 = 0,0521 0,06 (с)
Средняя абсолютная погрешность данной серии измерений равна:
![]()
Полученные результаты показывают, что абсолютные погрешности практически совпадают (по крайней мере, Т1, Т2, Т3 – числа одного порядка).
Поэтому нет необходимости считать и Т для каждого опыта. Можно ограничиться расчетом для одной строчки экспериментальных данных.
Результат можно представить в виде: Т = Тi Тi .
Т1 = (1,55 0,06) c;
Т2 = (1,79 0,06) c;
Т3 = (2,01 0,06) c.

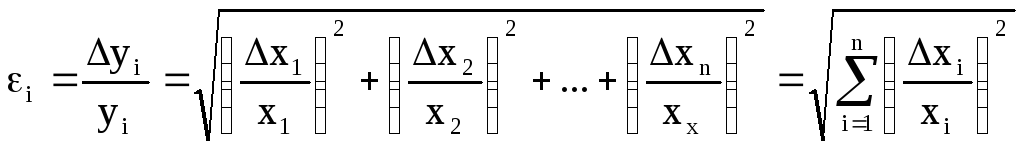 ,
(14)
,
(14)