4. Теория случайных погрешностей

4.1. Основные свойства случайных величин. Пусть Х_i – некоторая случайная величина, принимающая непрерывный ряд значений (Х₁, Х₂, Х₃, …,Х_n), которые подчиняются определенному закону распределения.

Функция Y =f (X_i), характеризующая вероятность попадания случайной величины Х_i в единичный интервал (Х=1), называется плотностью вероятности.

Вероятность того, что случайная величина Х_i попадает в интервал [X, (X  dX)], будет равна

Вероятность того, что случайная величина обнаруживается в интервале значений [X, (X  dX)], равна

.

Вероятность того, что случайная величина обнаруживается в интервале значений от - до +, равна 1, т.е. такое событие будет достоверным, а сама функция f(X) – нормируемой.

4.2. Функция распределения случайных величин и ее свойства.

Всякое соотношение, устанавливающее связь между возможными значениями, называется законом распределения случайных величин. Одним из наиболее распространенных является нормальный закон распределения (НЗР) Гаусса, для которого характерно то, что среднее арифметическое значение измеряемой величины является наиболее вероятным; другими словами, среднее арифметическое значение <X> является наилучшим приближением к истинному значению.

Закон Гаусса имеет вид:

(8)

где <X> - среднее арифметическое значение, определяемое по формуле (6);  - средняя квадратичная погрешность, определяемая по формуле:

, (9)

г

Рис.4

де X_i – результат i – измерения; (Х_i - <X>) – абсолютная погрешность отдельного измерения.

На рис.4 графически представлена зависимость f(Х). Как показали исследования, кривая распределения Гаусса симметрична относительно прямой Х = <X>, т.е. отклонения случайных величин X_i вправо и влево от <X> равновероятны (встречаются одинаково часто).

При Х = <X> плотность вероятности принимает максимальное значение, равное

(10)

При Х0 и Х кривая распределения асимптотически приближается к оси абсцисс (f(Х)0).

Средняя квадратичная погрешность (9) подбирается так, что при проведении большого числа серий измерений погрешность в 2/3 (67%) случаев меньше , а в 1/3 (33%) случаев она больше . Другими словами, если провести не одну, а например 10 серий по 10 опытов в каждой, то следует ожидать, что 67-70 случаях из ста (10х10) измерений среднее значение будет отличаться от истинного меньше, чем на  (Х < ), а в остальных 33-30% случаях Х > .

На рис.4 заштрихованная область составляет около 67% от всей площади под кривой, т.е. наиболее часто встречаются случайные величины Х_i в интервале [(<X>-); (<X>+)].

4.3. Доверительная надежность и доверительный интервал.

Вероятность того, что истинное значение содержится в интервале от (Х-) до (Х+), называется доверительной вероятностью (или надежностью). Графически эта надежность определяется как площадь под кривой распределения (рис.4) в интервале [(X-); (X+)]. Сам интервал значений случайных величин от (X-) до (X+) называется доверительным интервалом.

Погрешность, определяемая с надежностью   0,67, называется стандартной среднеквадратичной погрешностью _ст. Формула (9) позволяет хорошо оценивать величину стандартной погрешности, когда число опытов n  5. Целесообразность оценки погрешности с помощью формулы (9) объясняется тем, что _ст является одним из параметров в формуле Гаусса (8). Поэтому всегда можно рассчитать вероятность того, что результат измерения будет отличаться от <X> не более, чем на _ст.

Таким образом, для характеристики случайной погрешности измерений следует указывать не только случайную погрешность, но и надежность . Результат измерений в этом случае представляют в виде: X = <X>  _ст, (с надежностью   0,67), где _ст определяет абсолютную погрешность данной серии измерений. Это справедливо при малом числе опытов (n = 35).

От величины стандартной средней квадратичной погрешности зависит форма кривой распределения: чем меньше _ст, тем выше максимум функции распределения и тем более круто поднимается кривая f(X).

4.4. Критерий определения грубой погрешности в физическом эксперименте. Как уже указывалось, погрешность , определяемая формулой (9), подбирается так, что вероятность того, что результат измерения отличается от истинного не более, чем на  = _ст, равна 0,67. При этом Х  _ст, т.е. отношение  = Х/_ст = 1, а доверительная надежность  = 0,67.

В табл.3 приведены значения доверительной вероятности  при некоторых значениях отношений  ( = Х/_ст). Анализ этой таблицы показывает: вероятность того, что измеренная величина отличается от истинного на _ст, растет с увеличением абсолютной погрешности Х.

Из табл.3 видно, что при  = 1 (Х = _ст) надежность =0,67. Это означает, что в 67% случаев Х < _ст, а в остальных 33% случаев Х > _ст. Если  = 2 (Х = 2_ст), то вероятность того, что результаты измерений будут отличаться от истинного не более, чем на 2_ст, равна 0,95, т.е. 95% случайных погрешностей меньше 2_ст, а 5% - больше 2_ст. При  = 3 (Х = 3_ст) надежность  = 0,997.

Таблица 3

	0,9	1,0	1,5	1,7	2,0	2,5	3,0
	0,63	0,67	0,87	0,91	0,95	0,988	0,997

Условились считать, что если результат измерения Х_i отличается от среднего значения <X> больше, чем на 3_ст, то его отбрасывают как промах. Если Х < 3_ст, результат оставляют в ряду измеренных. Чаще всего при оценке погрешности измерений в физическом практикуме достаточной надежностью можно считать  = 0,95.

4.5. Формула для расчета случайной погрешности (формула Стьюдента). Данные, приведенные в табл.3, справедливы только для большого числа опытов (n > 30). Для оценки доверительной вероятности в случае малого числа опытов (n  30) вместо параметра  вводят параметр t_,n, зависящий от числа опытов n и надежности . Этот коэффициент называют коэффициентом Стьюдента. Он связан со средней квадратичной погрешностью соотношением:

(11)

Для данного числа опытов (n = const) и выбранной надежности ( = const) коэффициент Стьюдента имеет вполне определенное значение.

Значение t_,n приведены в табл.4. Сравнивая табл.3 и табл.4, можно убедиться, что с увеличением числа опытов значение коэффициента Стьюдента t_,n уменьшается, приближаясь к значению  (при заданном ).

При данном числе опытов (n = const) с ростом надежности  коэффициент Стьюдента растет. Вообще говоря, надежность выбирают произвольно, в зависимости от значимости проводимых измерений. Но можно договориться, например, при проведении физического практикума всегда выбирать  = 0,95.

Таблица 4

n	Надежность 
	0,63	0,70	0.80	0, 90	0,95	0,98	0,99
3	1,06	1,3	1,9	2,9	4,3	7,0	9,9
5	0,94	1,2	1,5	2,1	2,8	3,7	4,6
7	0,92	1,2	1,5	2,0	2,6	3,4	4,0
9	0,90	1,1	1,4	1,9	2,3	2,9	3,4
10	0,88	1,1	1,4	1,9	2,3	2,8	3,4
12	0,87	1,1	1,4	1,8	2,2	2,7	3,1
15	0,87	1,1	1,3	1,8	2,2	2,7	3,0
25	0,86	1,1	1,3	1,7	2,1	2,6	3,0

Анализ табл.4 показывает, что с ростом числа опытов (при заданной надежности ) коэффициент Стьюдента уменьшается, а, следовательно, уменьшается и абсолютная погрешность. Выразим Х из формулы (11), получим выражение для расчета случайной погрешности.

(12)

Подставив в последнее соотношение выражение для средней квадратичной погрешности (9), получим формулу расчета случайной абсолютной погрешности в общем виде.

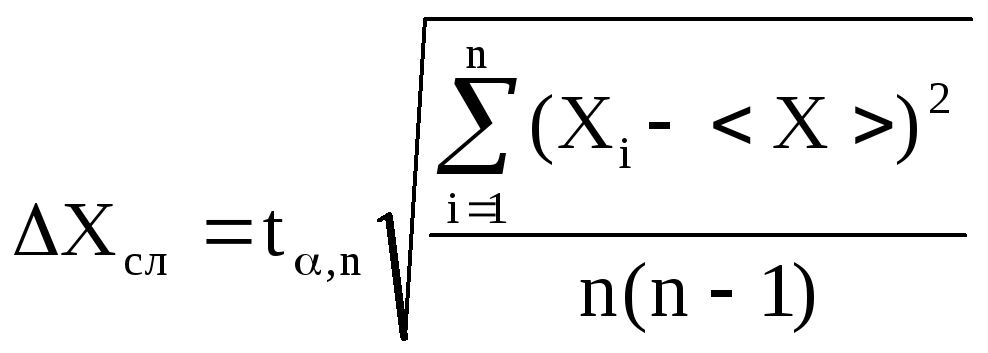(13)

Оценив случайную погрешность по формуле (13) и сравнив ее с инструментальной (приборной) погрешностью, студент должен решить, что принять за абсолютную погрешность эксперимента: либо Х_пр, либо Х_сл, либо искать полную погрешность по формуле (7).

4.6. Методика обработки случайных величин, полученных в физическом эксперименте. Пусть в результате эксперимента по измерению некоторой величины получен статистический ряд значений (Х₁, Х₂, Х₃,…,Х_i, …,Х_n). Чтобы наглядно представить, как часто появляются те или иные значения Х_i, необходимо построить диаграмму распределения случайных величин, которая называется гистограммой. Для этого статистический ряд значений записывают в упорядоченном виде (по мере возрастания или убывания элементов).

Рис.5

Далее весь диапазон значений от Х_max до X_min разбивают на К одинаковых интервалов шириной Х’=( Х_max - X_min)/К. Затем подсчитывают число m попаданий случайных величин в каждый из полученных интервалов. По оси абсцисс откладывают значения Х_i, а по оси ординат – число m попаданий случайных величин статистического ряда в каждый из интервалов и строят прямоугольники с основанием Х’ и высотой m. В результате такого построения получается ступенчатая диаграмма, называемая гистограммой (рис.5).

Как показывает опыт, максимальное число попаданий (заштрихованная область на рис.5) приходится на интервал в окрестности точки Х=<X>: [<X>-Х’/2, <X>+Х’/2].

Если увеличивать число опытов (n) и число интервалов, на которое разбивается статистический ряд (К), то в пределе Х’0 и вместо ступенчатой гистограммы получится плавная кривая распределения случайных величин (пунктирная линия на рис.5).