1. Определитель квадратной матрицы. Свойства определителей.

Определителем матрицы А называется число:

- матрица второго порядка.

Матрица 3-его порядка:

Свойства определителей:

1. если А и В – квадратные матрицы n*n, то:

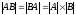
Замечание: АВВА

2.

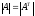
3. пусть А = (а_i,j) и при этом ее какой-либо ряд (либо столбец, либо строка) i-я строка обладает свойством, что:

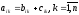4. определитель равен нулю, если в нем есть нулевой ряд.

5. определитель = 0, если у него есть два одинаковых (пропорциональных) параллельных ряда.

6. определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали.

7. определитель треугольной матрицы равен произведению чисел, стоящих на главной диагонали.

8. если в определителях поменять местами, то определитель поменяет знак.

9. если к какому-то ряду определителя прибавить элементы другого параллельного ряда, умноженные на какое-то число (одинаковое), то определитель при этом не изменяется.

10. если какой-то ряд определителя содержит в себе обдщий множитель, то его можно вынести за знак определителя. Обратная матрица

A^-1 =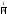A^*Т

Ранг матрицы. Способы нахождения.

Максимальное число линейно-зависимых строк матрицы A наз. рангом матрицы и обознач r(a). Наибольшее из порядков миноров данной матрицы отличных от 0 наз рангом матрицы.

Свойства:

1)при транспонировании rang=const.

2)если вычеркнуть нулевой ряд, то rang=const;

3)rang=cost, при элементарных преобразованиях.

3)для вычисл ранга с помощью элементар преобраз матрица A преобраз в матриц B, ранг которой легко находится.

4)ранг треуг матрицы=числу ненулевых элем, располож на глав. диагоналях.

Методы нахождения ранга матрицы:

1. метод окаймляющих миноров

2. метод элементарных преобразований

метод окаймляющих миноров:

метод окаймляющих миноров позволяет алгоритмизировать процесс нахождения ранг-матрицы и позволяет свести к минимуму количество вычисления миноров.

1. если в матрице все нулевые элементы, то ранг = 0

2. если есть хоть один ненулевой элемент => r(a)>0

теперь будем окаймлять минор М1, т.е. будем строить всевозможные миноры 2-ого порядка, ктр. содержат в себе i-тую строку и j-тый столбец, до тех пор, пока не найдем ненулевой минор 2-ого порядка.

М2 (i, i1, j.j1)

Дальше аналогично строим миноры 3-го порядка, окаймляющие М2 (минор), до тех пор, пока не получим минор, отличный от нуля.

Процесс будет продолжаться до одного из событий: 1. размер минора достигнет числа к.

2. на каком-то этапе все окаймленные миноры окажутся = 0.

В обоих случаях величина ранга-матрицы будет равна порядку большего отличного от нуля минора.

Метод элементарных преобразований: как известно, понятие треугольной матрицы определяется только для квадратных матриц. Для прямоугольных матриц аналогом является понятие трапецивидной матрицы.

Решение невырожденных СЛАУ методом Крамера:

Х=А^-1*В

А^-1=

X1=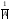(A₁₁b₁ + A₂₁b₂ + …+A_n1b_n)

Теорема: (Крамера): решение невырожденных уравнений АХ=В, 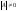можно записать так:

, Ак получается из А путем замены к-го столбца на столбец свободного члена В.

8. Метод Гаусса. Произвольные слау. Теорема Кронекера-Капелли.

Система уравнений (СУ), содерж m-уравнений и n-неизвестных наз. системой вида a₁₁x₁+a₁₂x₂+…+a_1nx_n=b₁ … a_M1x₁+a_M2x₂+…+a_Mnx_n=b_m, где a_ij – коэф системы и изменяется от 1 до n. Расширенной матрицей наз матрица, сост из исходной матрицы А и свободных .

Решением системы наз n значений неизвестных x₁=c₁ … x_n=c_n, при подстановке которых все ур-ия системы обращаются в верное равенство.

Система уравнений наз. совместной, если имеет хотя бы одно решение, иначе она несовместна. Совместная система наз. определённой, если она имеет единственное решение.

Системы наз. равносильными, если они имеют одно и то же решение.

Замечание: эквивалентные системы получаются при элементарных преобразованиях при условии, что преобраз вып только под строками.

СЛАУ наз однородной, если все свободные члены=0.

Теорема Кронекера-Капелли: система лин алг ур-ий совместна, когда rangA=rang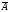(волнистая). Теорема: если rang совместной системы= числу неизвестных, то система имеет одно решение. Теорема: если ранг совмест сист < числа неизвестных, то система имеет бесконеч решений.

Правило решения СУ.

1)найти ранг основной и расширенной матрицы (если rA не =rA с крыш, то система несовместна.

2) если rA=rA с крыш и =r, то система совместна и надо найти базисный минор порядка r.

3)Берём r ур-ий из коэф которых составлен базисн минор. Остальные ур-ия отбрасываем. Неизвестные, коэф которых входят в минор наз главными. Из оставл слева, а остальные (n-r) – справа.

4)Найти выражения главных неизв через свободные. Получено общее решение системы

5)Придавая свободным низвестным произвольное значение, получим соотв значения главн неизв, т.е. найдём частные решения.

Векторы на плоскости и в пространстве. Операции над векторами.

Вектор – направленный отрезок, т.е. раз есть слово отрезок, значит есть начало и конец.

1. перенос отрезка при помощи параллельного переноса, не изменяет вектор.

2. вектор задается «длиной вектора» и направления.

3. если у вектора изменить направление на противоположное, то получаем противоположный вектор.

4. нулевой вектор – вектор, длина которого = 0 или начальная конечная точки совпадают. ( у нулевого вектора направление неопределенно).

Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой.

Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные.

Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости.

Примечание: два вектора в пространстве всегда компланарны.

Примечание: два вектора называются равными, если они сонаправлены и равны по длине.

Линейные операции над векторами:

1. Умножение вектора на число:

Результатом будет вектор, коллинеарный исходному (соноправленный в случае положительного множителя и противоположно-направленный – в случае отрицательного множителя), длина которого равна произведению модуля числового множителя на длину исходного модуля.