
III к. - Методы математической физики / Литература / Русак В.Н. Филиппова Н.К. - Задачи по математической физике и их решение
.pdfЗАДАЧИ ПО МАТЕМАТИЧЕСКОЙ ФИЗИКЕ
И ИХ РЕШЕНИЕ
Пособие для студентов физического факультета специальности 1-31 04 01 «Физика»
МИНСК
2006
А в т о р ы – с о с т а в и т е л и : В. Н. Русак, Н. К. Филиппова
Рекомендовано Ученым советом физического факультета
28 июня 2005 г.протокол №11
Р е ц е н з е н т ы :
доктор физико-математических наук, профессор В.Т. Ерофеенко; доктор физико-математических наук, профессор А. А. Пекарский.
Задачи по математической физике и их решения: пособие для студентов физ. спец. 1=310401 «Физика»/ авт.=сост. В.Н. Русак, Н.К. Филиппова. - Мн.: БГУ, 2006 г.-93 с.
Для студентов 1-2 курсов физического факультета и факультета радиофизики и электроники БГУ.
2
Предисловие Преподавание математических дисциплин на физических факультетах
Белорусского государственного университета складывалось на основе опубликованного В.И. Смирновым пятитомного «Курса высшей математики» 1 и серии учебных пособий 2 6 , отражающих опыт преподавания в московских вузах. Что касается непосредственно математической физики, то на русском языке также имеется ряд учебных пособий и сборников задач 7 15 .
В 1998 г. В.Н. Русак издал краткий курс математической физики рассчитанный на 90 лекционных часов. При написании настоящего пособия авторы, в доходчивой форме изложили круг основных идей и методов применяемых при решении задач математической физики в рамках действующей программы. В нем по каждой теме приведены необходимые теоретические сведения, подробно разобраны решения типовых упражнений и предложены примеры для самостоятельной работы. Основной ак - цент делается на метод разделения переменных и применение цилиндри - ческих функций.
Пособие адресовано студентам физикоматематических специальностей которые изучают дифференциальные уравнения в частных производных и их приложения.
3

§ 1. РЯДЫ И ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Если f(x) 2l– периодическая кусочно-гладкая функция раскладывается в ряд Фурье
a |
|
|
|
|
|
|
|
k x |
|
|
k x |
|
|
f (x 0) f (x 0) |
|
|||||
0 |
ak |
cos |
|
bk sin |
|
|
|
|
|
|
|
|
|
, |
||||||
2 |
l |
|
|
|
|
2 |
|
|
||||||||||||
k 1 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
l |
|
|
|
k x |
|
|
|
|
1 |
l |
|
k x |
|
|
|
|
k |
|
|
f (x) cos |
|
k |
|
|
f (x) sin |
dx. |
||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
a |
|
l |
|
|
l |
dx, b |
l |
|
l |
||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
l |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
на R, то она
x R, |
(1) |
|
(2) |
Бывает так, что функция f(x) задана и является кусочно-гладкой на отрезке -l, l и ее также можно разложить в ряд Фурье вида (1-2), и сумма этого ряда будет 2l – периодическим продолжением функции f(x). Добавим к сказанному, что в формулах (2) в силу 2l –периодичности можно вести интегрирование по любому отрезку длиной 2l.
Если f(x) четная 2l – периодическая кусочно-гладкая функция, то коэффициенты bk=0, и соответственно
a |
|
|
|
k x |
|
f (x 0) f (x 0) |
|
|
||||
|
k |
|
|
|
x R, |
|||||||
0 |
|
|
|
|
|
|
|
|
||||
a |
cos |
|
|
|
|
|
|
, |
||||
2 |
|
l |
|
|
2 |
|
||||||
|
k 1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 l |
|
|
k x |
|
|
|
|
|
|
|
a |
l |
|
f (x) cos |
l |
dx. |
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
(3)
(4)
Если f(x) нечетная 2l – периодическая кусочно-гладкая функция, то коэффициенты ak=0, и соответственно
|
k x |
|
f (x 0) f (x 0) |
|
||||
b sin |
(5) |
|||||||
|
|
|
|
|
||||
k |
l |
|
|
2 |
||||
k 1 |
|
|
|
|||||
|
|
|
|
|
|
|
||
|
2 l |
|
|
k x |
|
|
||
bk |
|
|
f (x)sin |
|
dx. |
(6) |
||
l |
l |
|||||||
|
|
|
||||||
|
|
0 |
|
|
|
|
|
|
Если f(x) кусочно-гладкая функция на отрезке 0, l , то ее можно разложить в ряд Фурье (3), (4), так и в ряд Фурье (5), (6), осуществляя соответствующее продолжение функции f(x).
Если f(x) непрерывная 2l – периодическая функция и существует кусочно-непрерывная производная f(x), то ряд Фурье функции f(x) сходится к ней равномерно.
Для всякой кусочно-непрерывной на -l, l функции выполняется равенство Ляпунова-Стеклова
a0 |
|
|
|
|
|
l |
|
|
ak2 bk2 |
|
1 |
|
f 2 (x)dx. |
|
|||
|
|
|
|
|
|
|||
2 |
|
l l |
(7) |
|||||
k 1 |
|
|
|
|||||
4

Если f(x) кусочно-непрерывная функция на отрезке -l, l , то ее ряд Фурье можно интегрировать почленно.
Предполагаем теперь, что f(x) определена на R, абсолютно интегрируема и является кусочно-гладкой на каждом конечном отрезке. Тогда справедлива интегральная формула Фурье
1 |
|
|
|
f (x 0) |
f (x 0) |
|
|
d |
f (t) cos (t x)dt |
. |
|||||
|
|
2 |
|||||
0 |
|
|
|
|
|||
|
|
|
|
|
|||
(8)
Разумеется, что в точках непрерывности правая часть соотношения (8) может быть заменена на f(x).
Интегральная формула Фурье равносильна выполнению двух преобразований: прямого преобразования Фурье
|
1 |
|
|
|
|
|
F ( ) |
|
f (t)e |
i t |
dt |
||
|
||||||
|
|
|||||
|
2 |
|
|
|
||
|
|
|
|
|
|
|
и обратного преобразования Фурье
|
1 |
|
|
|
|
|
f (x) |
|
f ( )e |
i x |
dx, |
||
|
||||||
|
|
|||||
|
2 |
|
|
|
||
|
|
|
|
|
|
|
(9)
(10)
где х точка непрерывности и интеграл в (10) понимается в смысле главного значения по Коши.
1. Разложить в ряд Фурье функцию
f (x) cos ax, |
a |
k |
, |
x ( l,l). |
|
l |
|||||
|
|
|
|
Р е ш е н и е. Учитывая четность f(x), применяем формулу (4) и получим при k 1
|
|
|
|
2 |
l |
|
|
|
|
k x |
|
1 |
l |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
a |
|
xdx |
|
|
||||
|
|
a |
l |
|
cos ax cos |
l |
l |
|
cos |
|
l |
|
|
||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
sin a |
|
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
k |
l |
|
|
|
|
|
k |
|
l |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
l |
|
|
k |
|
|
|
|
|
|
|
|
sin a |
|
x |
|
||||||||||
|
cos |
|
|
dx |
|
|
l |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|||||||
|
a |
|
x |
|
al k |
|
|
|
|
|
al k |
|
|||||||||||||||
|
l |
0 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
sin(al k ) |
|
sin(al k ) |
|
|
|
1 k |
2sin al |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
al. |
|
||||||||||||||
|
|
|
al k |
|
|
al k |
|
|
(al) |
2 |
(k ) |
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Если же k=0, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
l |
|
|
|
|
2sin al |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
cos axdx |
. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
a |
l |
|
|
|
al |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Cледовательно, на интервале
l,
cos ax 2al sin al
k 1
l |
выполнено равенство |
|
|||||
|
|
||||||
|
( 1)k |
cos |
k x |
|
sin al |
. |
|
(al)2 (k )2 |
l |
al |
|||||
|
|
|
|||||
2.Разложить в ряд Фурье функцию f(x) =arсsin(sin x), x R. Р е ш е н и е. Поскольку:
f x arcsin sin x arcsin sin x arcsin sin x f x ,
то f(x) нечетная функция на R, а период функции равен 2 . В качестве основного отрезка можно брать отрезок - , и применять формулу (6). Предварительно нужно учесть, что
|
|
|
|
|
|
f (x) arcsin(sin x) x, |
x |
|
0, |
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
Если же |
x |
|
, |
|
, |
то sin x=sin ( -x) и тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
f(x)=arcsin (sin( -x))= -x.
Следовательно для коэффициентов Фурье будем иметь по формулам
(6)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
bk |
|
|
|
x sin kxdx ( x) sin kxdx |
|
||
|
|||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
||||
|
|
x cos kx |
|
cos kxdx ( x) cos kx |
|
cos kxdx |
|
k |
0 |
||||||
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
cos k |
|
|
sin kx |
|
|
|
|
|
|||
|
k |
2 |
|
2 |
|
k |
|
|
|
|
|
|
|
|
|
2
0
|
|
cos k |
|
|
sin kx |
|
2 |
2 |
k |
||||
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
0, |
|
|
|
если k 2m, |
||
|
2 |
|
sin k |
sin k |
|
4 |
2 sin |
|
|
4( 1) |
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
m |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
2 |
|
|
2 |
k |
|
|
2 |
|
|
|
|
1) |
2 |
, |
если k 2m 1. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2m |
|
|
|
||||
Следовательно для всех x R имеет разложение в ряд |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
( 1) |
m |
|
|
|
|
|
|
|
|||
|
|
|
arcsin(sin x) |
|
|
|
|
|
sin(2m 1)x. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
m 0 (2m |
1) |
|
|
|
|
|
|
|
|||||||
3. Проверьте, что при 0<x< выполнено равенство |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
sin x |
|
sin 3x |
|
sin 5x |
|
|
x( x). |
|||||||||||
|
|
|
|
|
3 |
3 |
|
3 |
|
8 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|

Р е ш е н и е. Продолжим функцию
f (x) |
|
x( x) |
|
8 |
|||
|
|
нечетным образом на (- ,0) и разложим в ряд Фурье (5),(6). Будем иметь
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k |
|
|
|
|
( x x |
2 |
) sin kxdx |
|
|
|
|
x x |
|
( 2x) cos kxdx |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
b |
|
|
8 |
|
|
4k |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
( 2x)d sin kx |
|
|
2 |
|
( 2x) |
|
|
|
|
2 |
|
sin kxdx |
|
|
|
|
||||||||||||
|
|
|
4k |
|
|
|
|
|
|
|
|
4k |
|
|
|
sin kx |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0, |
|
|
если k 2m |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
( 1)k 1 1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
cos kx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2k3 |
|
|
2k3 |
|
|
|
|
|
|
|
|
, если k 2m 1, |
m 0, . |
|||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2m 1) |
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, мы проверили, что
b |
|
1 |
|
, |
|
3 |
|||
2m 1 |
|
(2m 1) |
|
|
|
|
|
|
b |
0, |
2m |
|
и тем самым устано-
вили нужное равенство.
4. Разложите в ряд Фурье функцию
f (x) |
a sin x |
|
, |
a 1. |
|
1 2a cos x a |
2 |
||||
|
|
|
|||
|
|
|
|
Р е ш е н и е. Поскольку f(x) определена на R, нечетная, имеет период 2 и является гладкой, то она разлагается в ряд (5),(6), однако коэффициенты будем находить не по формулам (6). Воспользуемся известным степенным рядом
1 |
|
1 |
ae |
ix |
a |
2 |
e |
2ix |
a |
n |
e |
inx |
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
1 ae |
ix |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Левую часть равенства в числителе и знаменателе домножим на тогда будем иметь
1 ae |
ix |
|
|
|
||
|
a |
n |
(cos nx i sin nx), |
|||
|
|
|
|
|||
1 a |
2 |
2a cos x |
|
|||
|
n 0 |
|
|
|||
|
|
|
|
|
|
|
и если в этом соотношении отделить слева и справа мнимые получим
|
a sin x |
|
|
|
|
|
|
||
|
1 a |
n |
sin nx. |
|
|
||||
|
|
|
|
|
|||||
1 a |
2 |
2a cos x |
|
|
|
||||
|
n 1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
5. Найдите преобразование Фурье для функции |
f (x) |
|
1 |
, |
|||||
|
|
||||||||
a2 |
x2 |
||||||||
|
|
|
|
|
|
|
|||
|
ix |
, |
1 ae |
|
|
части, то
a 0.
Р е ш е н и е. Пользуясь формулой (9) и леммой Жордана будем иметь при >0
7
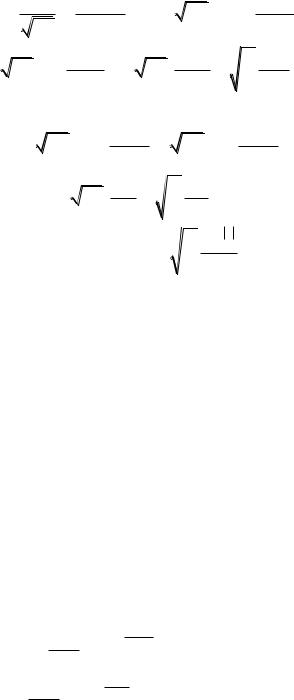
|
1 |
|
|
e |
i t |
|
|
|
|
|
|
|
e |
i t |
|
|
||
F ( ) |
|
|
|
|
dt |
|
2 i |
Re s |
|
|
|
|||||||
2 |
a |
2 |
t |
2 |
|
t ai |
||||||||||||
|
|
|
|
|
|
|
|
t ai |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
e |
i t |
|
|
|
e |
a |
|
e |
a |
|
|
||||
2 i lim |
|
|
|
2 i |
|
|
|
. |
|
|||||||||
|
|
|
|
2ai |
|
|
|
|
||||||||||
|
t ai |
t |
ai |
|
|
|
|
2 |
|
a |
|
|
||||||
Если же <0, то интеграл считается через вычет в точке ai и получим
|
|
|
e |
i t |
|
|
|
|
|
e |
i |
||
F ( ) |
2 i Re s |
|
|
|
|
2 i lim |
|
||||||
t ai |
|
t |
|||||||||||
|
|
t ai |
|
|
|
|
t ai |
||||||
|
|
|
e |
a |
|
|
e |
a |
|
|
|
||
|
|
2 i |
|
|
|
|
|
. |
|
|
|||
|
2ai |
|
2 |
a |
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
e |
a |
|
|
|
Объединяя обе формулы, найдем |
F ( ) |
|
|
. |
|
||||||||
|
2 |
a |
|
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Разложите в ряды Фурье в указанных интервалах:
6.f(x)=x в интервале (-l, l).
7.f(x)= signx в интервале (-l, l).
8.f(x)=cos4x, x (- , ).
9.f(x)=|x|, x (-l, l).
10.f(x)=l2-x2 в интервале (-l, l) .
11. f(x)=x2 в интервале (- , ).
t
ai
|
|
2x, |
если |
x 0 . |
|
12. |
f x |
||||
|
|
|
|||
|
3x, если |
0 x |
|||
13.f(x)= |sinx|, x (- , ).
14.f(x)= |cosx|, x (- , ).
15.f(x)=sign(cosx) , x (- , ).
16.f(x)=arcsin(cosx) , x (- , ).
17.f(x)=x- x , x (- , ).
18.Функцию f(x)=x2 разложить в ряд Фурье
а) по косинусам |
cos |
k x |
, |
k 0, , |
||||
|
l |
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
б) по синусам |
sin |
k x |
, |
k |
1, , |
|||
l |
|
|||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
в) в интервале (0,2l).
Используя эти разложения, найти суммы числовых рядов
8

|
1 |
|
|
( 1) |
k 1 |
|
|
1 |
|
||
|
, |
|
|
, |
|
2 . |
|||||
k |
2 |
k |
2 |
(2k 1) |
|||||||
k 1 |
|
|
k 1 |
|
|
|
k 1 |
|
|||
|
|
|
|
|
|
|
|
|
|||
19. Отправляясь от разложения
|
|
|
|
|
sin |
k x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2l |
|
|
|
|
|
|
, |
|
x |
|
|
( 1) |
k 1 |
|
l |
, |
l x l |
|
|
|
|
|
||||||
|
|
|
|
k |
|
||||
|
k 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
найти интегрированием разложения в ряд Фурье на интервале функций х2, х3, х4.
20. Напишите равенство Ляпунова для функции
0, |
если x , |
|
|
f (x) |
если x . |
1, |
|
|
|
21. Вычислить с помощью равенства Ляпунова интеграл
l, l
|
|
|
(cos x cos 2x ... cos nx) |
2 |
dx. |
|
||
|
|
|
Найдите разложения в ряды Фурье с помощью степенных рядов для следующих 2 -периодических функций:
22. 23. 24.
|
1 a |
|
|
|
2 |
|
|
f (x) |
1 2a cos x a |
2 |
, a 1, |
|
|
||
|
|
|
f (x) |
1 a cos x |
|
, |
|
a 1, |
|
1 2a cos x a |
2 |
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
f (x) ln 1 2a cos x a |
2 |
, |
a |
|||
|
||||||
x( , ).
x( , ).
1, x ( , ).
Докажите равенства:
|
|
|
|
|
x |
|
|
|
|
cos nx |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
25.ln |
sin |
|
ln 2 |
, |
x ( , ). |
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
n |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x |
|
|
|
|
( 1) |
n 1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
26.ln |
cos |
ln 2 |
|
cos nx, x |
( , ). |
|
|
|
|
||||||||||||||
2 |
|
n |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
cos 2x |
|
|
cos 4x |
|
cos 6x |
|
|
|
|
|
||||||
27. |
|
|
4 sin x |
|
|
|
|
|
|
|
...; x (0, ). |
|
|
|
|
||||||||
2 |
1 3 |
|
|
3 5 |
5 7 |
|
|
|
|
||||||||||||||
28. Как нужно продолжить функцию f(x) с интервала |
|
0, |
|
на интервале |
|||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(- , ), чтобы выполнялось равенство f (x) bn sin(2n 1)x ? |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
29. Как нужно продолжить функцию f(x) с интервала |
|
0, |
|
на интервал |
|||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|

(- , ), чтобы выполнялась равенство
f(x) an cos(2n 1)x. n 1
Найдите преобразования Фурье от следующих функций:
|
1, |
|
|
если |
|
|
|
|
x |
|
|
1, |
|
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30. |
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
||||||||||||||
|
0, |
|
|
|
если |
|
|
|
|
x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sgn x, |
если |
|
|
|
x a, |
|
|||||||||||||||||||||||||||||
31. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
0, |
|
|
|
если |
|
|
|
x a. |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32. f (x) sgn( x 1) sgn( x 2). |
|
|||||||||||||||||||||||||||||||||||
|
1 |
|
x |
|
, если |
|
|
|
x |
|
|
|
1, |
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33. |
f (x) |
0, |
|
|
|
если |
|
|
|
x |
|
1. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x, |
если |
|
|
x |
|
|
|
|
, |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34. |
f (x) |
0, |
|
|
|
|
|
если |
|
|
x |
|
|
|
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
cos wt, если |
|
|
|
t |
|
|
, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
2a |
||||||||||||||||||||||||||||||
35. |
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0, |
если |
|
t |
|
|
|
|
|
. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2w |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
36. |
f (x) e |
2 |
|
x |
|
, |
|
|
|
x ( , ). |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37. |
f (x) xe |
a x |
, |
a 0, x ( , ). |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38. Найдите четное и нечетное преобразование Фурье для функции
f (x) e |
x |
, |
x (0, ), |
продолжая ее четным или нечетным способом. |
|
||||
|
|
|
|
10
