
уч.пос.1 (1)
.pdf
Задача №15. Выбрать все правильные ответы.
а)  - инъективно. б)
- инъективно. б)  -сюръективно. в)
-сюръективно. в)  -биективно.
-биективно.
г) а)-в)-неверны.
а) Отображение 


 по правилу
по правилу




Решение:



 отображение
отображение  не является инъективным.
не является инъективным.
Ответ: г).
б) Отображение 




 по правилу
по правилу 




Решение:



 отображение
отображение  не является инъективным.
не является инъективным.






 отображение
отображение  сюръективно
сюръективно
Ответ: б).
в) Отображение 




 по правилу
по правилу 




Решение:
Функция  монотонна на отрезке
монотонна на отрезке 


 отображение
отображение  инъективно.
инъективно.
Ответ: а).
21

г) Отображение 






 по правилу
по правилу 
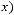



Решение:
Функция  монотонна на отрезке
монотонна на отрезке 


 отображение
отображение  инъективно.
инъективно.









 отображение
отображение  сюръективно
сюръективно
Значит,  – биекция.
– биекция.
Ответ: а),б),в).
5. Мощность множеств.
Теоретические сведения:
Два множества 

 имеют одинаковую мощность, если они эквивалентны, то есть существует биекция
имеют одинаковую мощность, если они эквивалентны, то есть существует биекция 


 .
.
Мощностью конечного множества называется количество элементов этого множества, то есть если 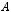






 , то
, то 



 .
.
Говорят, что множество  имеет счетную мощность
имеет счетную мощность 




 , если оно эквивалентно множеству натуральных чисел
, если оно эквивалентно множеству натуральных чисел  .
.
Критерий счетности множества: множество  имеет счетную мощ-
имеет счетную мощ-
ность  элементы множества
элементы множества 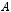 можно перенумеровать, используя все натуральные числа.
можно перенумеровать, используя все натуральные числа.
Из любого бесконечного множества можно выделить счетное подмножество.
Любое бесконечное подмножество счетного множества является счетным.
Объединение конечного или счетного набора счетных множеств является счетным множеством.
22

Декартово произведение конечного набора счетных множеств является счетным множеством.
Пусть  - бесконечное множество,
- бесконечное множество,  – конечное или счетное, тогда
– конечное или счетное, тогда  эквивалентно
эквивалентно 

 .
.
Пусть  - бесконечное несчетное множество,
- бесконечное несчетное множество,  – конечное или счетное, тогда
– конечное или счетное, тогда  эквивалентно
эквивалентно 
 .
.
Говорят, что множество  имеет мощность континуума
имеет мощность континуума 




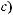 , если оно эквивалентно интервалу (0,1).
, если оно эквивалентно интервалу (0,1).
Объединение конечного или счетного набора множеств мощности континуума имеет мощность континуума.
Декартово произведение конечного или набора множеств мощности континуума имеет мощность континуума.
Говорят, что мощность множества  больше мощности множества
больше мощности множества  , если
, если  эквивалентно некоторому подмножеству в
эквивалентно некоторому подмножеству в  и при этом
и при этом  не эквивалентно никакому подмножеству в
не эквивалентно никакому подмножеству в  .
.
Любые два множества сравнимы по мощности.
Обозначим через 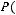
 множество, состоящее из всех подмножеств множества
множество, состоящее из всех подмножеств множества  . Тогда
. Тогда 






 .
.
Мощность множества 


 будем называть мощностью гиперконтинуума и обозначать
будем называть мощностью гиперконтинуума и обозначать  .
.
Мощность любого конечного множества меньше мощности любого бесконечного множества. Имеют место следующие неравенства: 



 .
.
Задача №16. Какую мощность имеет множество 
 ?
?
а) |
счѐтную |
б) |
континуума |
в) |
гиперконтинуума |
г) |
конечную |
д) |
а)-г) неверны |
23

Решение:
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: б). |
|
|
|
|||||||
Задача №17. Сравнить мощности множеств |
и : |
|||||||||
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
б) |
|
|
|
; |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
в) |
|
|
|
; |
A= , В= . |
|
|
|
|||||||
Решение: |
|
|
|
|||||||






 .
.
Ответ: в).
24

Список задач для самостоятельного решения
Задача №1.Определите, какое множество заштриховано на рисунке:
Задача№2. Даны множества: А=

 , В=
, В=

 , С=
, С=
 . Найти сумму элементов заданного множества.
. Найти сумму элементов заданного множества.
Задача №3. Выбрать множество равное заданному множеству.
Задача №4. Заданы множества А,В,С. Нужно выбрать верный вариант ответа из предложенных.
Задача №5. Нужно определить, какое множество заштриховано на рисунке. (Задача на декартово произведение множеств).
Задача №6-10. Различные комбинаторные задачи.
Задача №11. Задачи на формулу включений и исключений для трех множеств.
Задача №12. На множестве А задано бинарное отношение  . Нужно определить, какими свойствами оно обладает.
. Нужно определить, какими свойствами оно обладает.
Задача №13-14. Задачи на определение образа и прообраза заданного отображения.
Задача №12.
Задача №15. Задано отображение. Необходимо определить, является ли оно инъективным, сюръективным, биективным.
Задача №16. Определить мощность заданного множества.
Задача №17. Сравнить мощности двух множеств.
6. Задачи для самостоятельного решения
Задача №1.Определите, какое множество заштриховано на рисунке:
25

а)




б)




1) в)




г) 




а) 




б) 




в) 







2)
г) 



 ;
;
а) 



б) 











 ;
;
3)
г) 



 а)
а) 




б) 



в)
4)
г) 



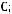 а)
а) 




б) 



 ;
;
в) 




5)
г) 






26

а) 




б) 







в) 




6)
г) 



 а)
а) 






б) 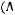




в) 



7)
г) 






 а)
а) 




б) 




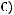

в) 



8)
г) 







а) 



 ;
;
б) 

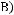


в) 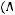

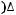

9)
г) 



 ; а)
; а) 




б) 

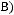


в) 

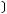



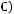

10)
г) 



 а)
а) 







б) 






в) 



 ;
;
11)
г) 




27

а) 







б) 
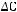





в) 



 ;
;
12)
г) 



 а)
а) 




б) 



 ;
;
в)
13)
г) 




а) 

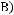

 ;
;
б) 






в) 



14)
г) 




а) 
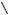


 ;
;
б) 







в) 




15)
г) 



 а)
а) 




б) 


 ;
;
в) 




16)
г) 




28

а)





 ;
;
б) 




в) 



 ;
;
17)
г) 




а)





 ;
;
б) 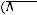




в) 




18)
г) 



 а)
а) 





б) 






в) 


 ;
;
19)
г) 





а)





 ;
;
б) 




в)
20)
г) 


 ;
;
а) 


 ;
;
б) 







в)





 ;
;
21)
г) 




 а)
а) 




б) 



 ;
;
в)
22)
29

а)



 ;
;
б) 




в)
23)
г) 




 а)
а) 




б) 




в) 




24)
г) 




30
