
уч.пос.1 (1)
.pdf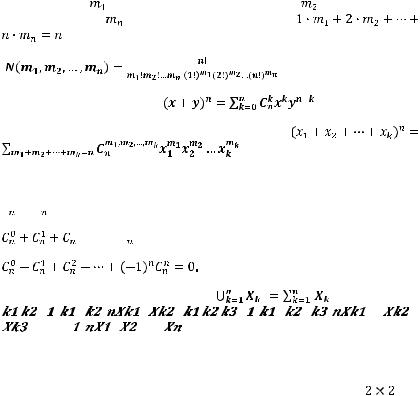
Количество неупорядоченных разбиений множества, состоящего из n
элементов, |
на |
одноэлементных подмножеств, |
|
двухэлементных |
||
подмножеств, …, |
|
n-элементных подмножеств ( |
|
|
||
): |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||
Формула бинома Ньютона: |
|
. |
||||
|
||||||
Обобщение |
формулы бинома Ньютона: |
|
|
|||
|
|
. |
|
|
|
|
Свойства биномиальных коэффициентов:


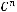

 ;
;



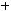
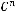

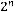 ;
;
|
|
|
|
|
|
|
|||
Формула включений и исключений: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
, = ( < |
) |
∩ + , , = ( < < ) |
∩∩ ∩ |
||||||
−…+(− ) |
∩ |
∩…∩ . |
|
||||||
Задача №6. а) Сколько способов раскрасить клетки таблицы |
, се- |
||||||||
мью цветами радуги? |
|
|
|
|
|
|
|
|
|
Решение:
Для каждой клетки существует семь способов раскраски. Тогда число способов раскрасить клетки таблицы 

 , семью цветами радуги равно
, семью цветами радуги равно



 2401.
2401.
Ответ: 2401.
б) Сколько способов раскрасить клетки таблицы 

 , семью цветами радуги так, чтобы все клетки имели различные цвета?
, семью цветами радуги так, чтобы все клетки имели различные цвета?
11

Решение:
Для первой клетки существует семь способов раскраски, для второй - 6, для третьей – 5, для четвертой - 4. Тогда число способов раскрасить
клетки таблицы 

 , семью цветами радуги равно
, семью цветами радуги равно 

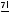
 840.
840.
Ответ: 840.
в) Сколько способов выбрать 4 карандаша из набора, содержащего 7 разноцветных карандашей?
Решение:
Количество способов выбрать 4 карандаша из набора, содержащего 7 разноцветных карандашей, равно числу сочетаний из 7 по 4 без повторений:
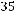 .
.
Ответ: 35.
г) Сколько способов выбрать 4 карандаша из 4 одинаковых наборов, содержащих 7 разноцветных карандашей каждый?
Решение:
В данном случае мы выбираем неупорядоченные наборы с повторениями.

 .
.
Ответ: 210.
д) В буфете продаются яблочный, апельсиновый и томатный соки, а также бутерброды с колбасой и бутерброды с сыром – все по 10 рублей. Сколько способов позавтракать в буфете соком и бутербродом, если у вас всего 20 рублей?
12

Решение: С каждым видом сока можно купить один из двух бутербродов. По правилу произведения получаем 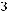

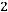

 способов.
способов.
Ответ: 6.
е) В буфете продаются яблочный, апельсиновый и томатный соки, а также бутерброды с колбасой и бутерброды с сыром – все по 10 рублей. Сколько способов купить в буфете сок или бутерброд, если у вас всего 10 рублей?
Решение: По правилу суммы получаем 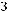



 способов.
способов.
Ответ: 5.
Задача №7. а) Сколько способов выложить в ряд 5 одинаковых вилок, 3 одинаковых ножа и 2 одинаковые ложки?
Решение:
Если бы все предметы были различными, то количество их перестановок было бы (5+3+2)!=10! При перестановках одинаковых предметов между
собой ничего не меняется. Получаем 

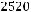

Ответ: 2520.
б) Сколько способов переставить буквы в слове «математика»?
Решение:
Если бы все буквы были различными, то количество их перестановок было бы 10! При перестановках одинаковых букв между собой ничего не меняется. В нашем слове 2 буквы «м», 3 буквы «а», 2 буквы «т». По-
лучаем 



Ответ: 151200.
в) Сколько способов связать бусы из 20 разноцветных бусинок?
Решение:
13

Количество способов выложить бусинки в ряд равно 20! При выкладывании бусинок по кругу любое их расположение, получающееся из како- го-то одного 19 поворотами, следует считать одним и тем же вариантом.
Получаем  =19! При связывании бус их можно еще и переворачивать.
=19! При связывании бус их можно еще и переворачивать.
Перевороты сокращают количество бус в 2 раза:  .
.
Ответ: 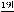 .
.
г) Сколько существует четырехзначных чисел, все цифры которых не делятся на 4?
Решение:
Цифры, которые не делятся на 4: 1,2,3,5,6,7,9. Всего их 7 штук. То есть каждую из четырех цифр числа можно выбрать семью способами. Получаем 


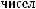

Ответ: 2401.
д) Сколько делителей у числа 400?
Решение:
400=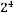

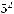 . В разложении делителя на простые множители 2 может иметь одну из степеней: 0,1,2,3,4, а 5 может иметь одну из степеней: 0,1,2. Получаем 5*3=15 делителей.
. В разложении делителя на простые множители 2 может иметь одну из степеней: 0,1,2,3,4, а 5 может иметь одну из степеней: 0,1,2. Получаем 5*3=15 делителей.
Ответ: 15.
Задача №8. Найти сумму корней уравнения: 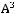
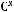



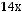

Решение:
14








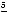 не являются корнями исходного уравнения.
не являются корнями исходного уравнения.



 корень.
корень.
Ответ: 5.
Задача №9. Определите наименьшее z из условия, что разность между
членами разложения 
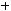

 , содержащими соответственно
, содержащими соответственно  и z4, равна 300.
и z4, равна 300.
Решение:
По условию

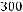 ,
,
Ответ: -2.
15

Задача №10. Компания, состоящая из 8 супружеских пар, разбивается на 4 группы по 4 человека для лодочной прогулки. Сколькими способа можно разбить их так, чтобы в каждой лодке оказались 2 мужчины и 2 женщины?
Решение:
Количество упорядоченных разбиений восьми мужчин по четырем лодкам равно 

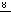 . Количество упорядоченных разбиений восьми
. Количество упорядоченных разбиений восьми
женщин по четырем лодкам также равно 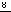 . Тогда число упорядоченных разбиений восьми мужчин и восьми женщин по четырем лодкам
. Тогда число упорядоченных разбиений восьми мужчин и восьми женщин по четырем лодкам
равно 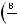


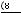
 . Число неупорядоченных разбиений восьми мужчин и восьми женщин по четырем лодкам равно
. Число неупорядоченных разбиений восьми мужчин и восьми женщин по четырем лодкам равно 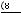
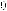

 .
.
Ответ: 264600.
Задача №11. В объединении множеств А, В и С 20 элементов. Множество А содержит 12 элементов , множество В – 13 элементов, множество С – 14 элементов. В пересечении множеств А, В и С – 4 элемента. Сколько элементов содержится ровно в двух множествах?
Решение:
Формула включений и исключений для трех множеств:
Количество элементов, содержащихся ровно в двух множествах:
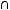
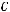


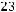

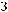


 11.
11.
Ответ: 11.
16

3. Бинарные отношения на множествах.
Теоретические сведения:
Говорят, что на множестве A задано бинарное отношение  , если в декартовом квадрате
, если в декартовом квадрате 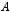

 выделено некоторое подмножество
выделено некоторое подмножество  ,
,
называемое определяющим |
множеством |
отношения . Элементы |
|
состоят в отношении |
( |
, если |
. |
Бинарное отношение 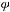 на множестве
на множестве 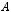 называется
называется
а) рефлексивным, если 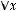




б) иррефлексивным, если 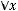
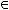


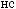
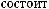


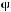

 ;
;
в) симметричным, если 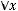


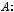

г) антисимметричным, если 
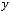
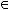

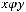


д) транзитивным, если 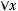
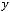

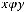


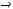

е) отношением типа эквивалентности, если оно рефлексивно, симмет-
рично и транзитивно;
ж) отношением частичной упорядоченности, если оно рефлексивно,
антисимметрично и транзитивно.
Задача №12. На множестве А задано бинарное отношение  . Выбрать все правильные утверждения.
. Выбрать все правильные утверждения.
а) |
рефлексивно. |
б) |
симметрично. |
в) |
антисимметрично. |
г) |
транзитивно. |
д) |
является отношением частичной упорядоченности. |
е) |
является отношением типа эквивалентности. |
ж) |
иррефлексивно. |
А= , |
. |
|
17 |

Решение:
Рефлективность. 

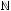





Иррефлексивность. Для 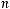









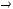 отношение
отношение 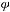 не является иррефлексивным.
не является иррефлексивным.
Симметричность. Если 
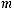
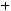
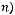
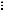
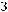 то
то 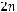



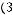

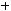


 ) 3
) 3
Антисимметричность. Для 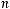



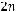
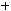
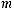

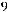

 но
но 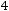
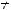
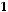
 отношение
отношение 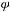 не является антисимметричным.
не является антисимметричным.
Транзитивность. Если 




 и
и 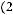
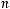
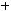


 , то
, то
Отношение 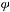 рефлексивно, симметрично и транзитивно
рефлексивно, симметрично и транзитивно 
 является отношением типа эквивалентности.
является отношением типа эквивалентности.
Отношение  не является антисимметричным
не является антисимметричным 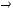
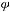 не является отношением частичной упорядоченности.
не является отношением частичной упорядоченности.
Ответ: а,б,г,е.
4. Отображения.
Теоретические сведения:
Говорят, что задано отображение  , действующее из множества
, действующее из множества 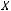 в множество
в множество  (
(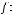
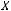
 ), если каждому элементу
), если каждому элементу 
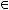
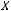 поставлен в соответствие единственный элемент
поставлен в соответствие единственный элемент 
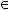
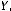 Элемент
Элемент 

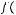
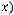 называется образом элемента
называется образом элемента  .
.
Образ множества 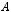

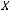 :
: 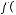




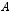

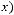

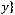

18
Прообраз множества 

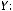
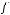

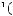
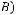

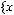
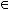


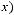
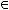


Отображение 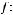


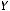 называется инъективным, если
называется инъективным, если
Отображение 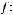

 называется сюръективным, если
называется сюръективным, если
Отображение 


 называется биективным, если оно инъективно и сюръективно.
называется биективным, если оно инъективно и сюръективно.
Задача №13. а) Отображение  :
:  по правилу
по правилу 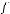 (
( )=
)=

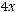


Найти образ отрезка 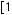
 .
.
а) [1,5]; б) {1}; в) [1,2]; г) [0,2];
д) (-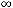
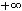 ).
).
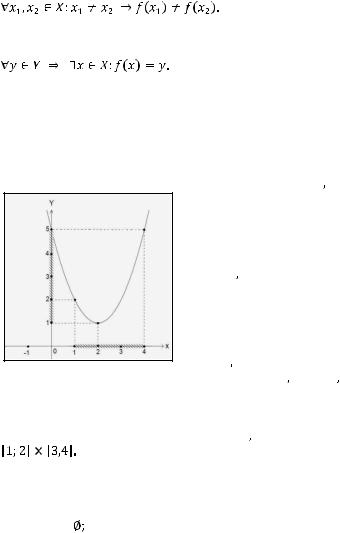
Решение: Построим график функции
 (
( )=
)=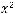



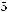 .
.
Минимальное значение функции на отрезке 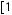
 равно 1, максимальное зна-
равно 1, максимальное зна-
чение равно 5. Функция непрерывна. Значит, 



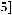

Ответ: а.
б) Отображение  :
: 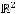
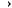 по правилу
по правилу 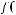

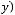


 . Найти образ
. Найти образ
а) [4;10]; б) [6;7]; в) [5;8];
г)
д) .
19
Решение:
Минимальное значение функции 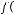

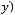 на квадрате
на квадрате 




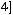 равно
равно 

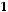



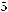 , максимальное значение равно
, максимальное значение равно 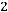





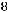 . Функция непрерывна. Значит,
. Функция непрерывна. Значит, 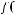


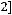

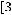



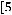
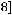

Ответ: в.
Задача №14. Отображение 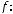
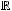
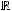 по правилу
по правилу 
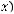

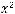


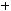

 Найти прообраз ,-1;2].
Найти прообраз ,-1;2].
а) [1;3]; б) [1;2]; в) [-1;3]; г) [-1;2]; д) [0;1];
Решение:
Построим график функции  (
( )=
)=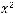

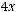

 .
.
Ответ: а.
20
