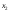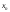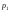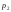- •Часть 1 введение Лекция 1
- •Основные понятия теории вероятностей
- •Часть 2
- •Лекция 3
- •Условная вероятность и независимость событий.
- •Формула полной вероятности
- •И теорема Байеса
- •Часть 3
- •Последовательность независимых испытаний
- •Лекция 4
- •Независимые испытания. Формула бернулли. Асимптотические формулы муавра – ЛаплАса и пуассона
- •Часть 4 случайные величины Лекция 5
- •Случайные величины. Законы распределения случайных величин
- •Закон распределения. Ряд распределения
- •Дискретной случайной величины
- •Лекция 6
- •Числовые характеристики
- •Случайных величин
- •Лекция 7
- •Распределения дискретных случайных величин
- •Лекция 8
- •Распределения непрерывных случайных величин
- •Часть 5
- •Лекция 10
- •Числовые характеристики системы двух случайных величин. -мерный случайный вектор
- •Часть 6 функции случайных величин Лекция 11
- •Закон распределения и числовые характеристики функций случайных величин
- •Лекция 12
- •Характеристическая функция
- •Часть 7 предельные теоремы теории вероятностей Лекция 13
- •Закон больших чисел и центральная предельНаЯ теорема
- •Часть 8 математическая статистика Лекция 14
- •Основные понятия и задачи математической статистики
- •Лекция 15
- •Статистическое оценивание параметров распределения
- •Лекция 16
- •Проверка статистических гипотез
Часть 7 предельные теоремы теории вероятностей Лекция 13
Закон больших чисел и центральная предельНаЯ теорема
ЦЕЛЬ ЛЕКЦИИ: доказать неравенство Чебышева; сформулировать и доказать закон больших чисел и его следствия; доказать центральную предельную теорему для случая суммы независимых случайных величин.
Закон больших чисел утверждает, что среднее арифметическое большого числа случайных величин ведет себя как среднее арифметическое их математических ожиданий. А согласно центральной предельной теореме достаточно большая сумма сравнительно малых случайных величин ведет себя как нормальная случайная величина. Различные формы закона больших чисел вместе с различными вариантами центральной предельной теоремы образуют совокупность так называемых предельных теорем теории вероятностей и имеют большой практический смысл, так как составляют теоретическую основу математической статистики.
В качестве леммы, необходимой для доказательства теорем, относящихся к группе "предельных", докажем неравенство Чебышева.
Неравенство Чебышева
Если
у случайной величины
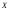 известна дисперсия
известна дисперсия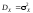 ,
то она в некотором смысле является мерой
"случайности" величины
,
то она в некотором смысле является мерой
"случайности" величины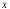 .
.
Так, для случайной величины, имеющей равномерный закон распределения
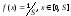 ,
,
дисперсия равна
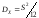 .
.
При
малых
 мала и дисперсия, но невелико и отличие
любого значения случайной величины от
ее математического ожидания.
мала и дисперсия, но невелико и отличие
любого значения случайной величины от
ее математического ожидания.
Аналогично
для нормального распределения: чем
больше дисперсия, тем больше область
вероятных (имеющих отличные от нуля
вероятности) значений случайной величины
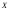 ,
хотя и с меньшей вероятностью.
,
хотя и с меньшей вероятностью.
Таким
образом, чем больше величина дисперсии
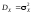 ,
тем более вероятны значительные
отклонения возможных значений случайной
величины от центра группирования –
математического ожидания
,
тем более вероятны значительные
отклонения возможных значений случайной
величины от центра группирования –
математического ожидания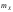 .
.
Если
у случайной величины
 известна плотность распределения
известна плотность распределения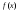 ,
то для любого положительного
,
то для любого положительного можно вычислить вероятность события
вида
можно вычислить вероятность события
вида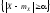 .
.
Однако
чаще встречается вариант, когда при
неизвестном законе распределения, но
по известной дисперсии
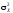 необходимо оценить вероятность события
необходимо оценить вероятность события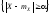 .
Эту задачу решил Чебышев Пафнутий
Львович (1821–1894) посредством неравенства,
названного его именем.
.
Эту задачу решил Чебышев Пафнутий
Львович (1821–1894) посредством неравенства,
названного его именем.
Неравенство
Чебышева. Для любой случайной
величины, имеющей конечную дисперсию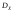 и математическое ожидание
и математическое ожидание ,
для любого положительного
,
для любого положительного имеет место неравенство
имеет место неравенство
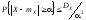 .
.
Доказательство.
Для дискретной случайной величины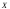 ,
заданной рядом распределения
,
заданной рядом распределения
|
Х: |
|
|
… |
|
|
|
|
|
… |
|
, |
изобразим возможные значения этой величины на числовой оси в виде точек (см. рис. 7.1).
Зададимся
некоторым значением
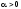 и вычислим вероятность того, что случайная
величина
и вычислим вероятность того, что случайная
величина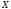 отклонится от своего математического
ожидания
отклонится от своего математического
ожидания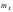 на величину, большую чем
на величину, большую чем :
:
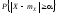 ,
,
т.
е. вероятность того, что
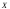 попадет
не внутрь отрезка
попадет
не внутрь отрезка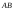 ,
а вне его,
,
а вне его,
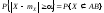 .
.
Чтобы
вычислить эту вероятность, необходимо
просуммировать вероятности всех значений
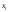 ,
которые лежат вне отрезка
,
которые лежат вне отрезка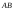 ,
т. е.
,
т. е.
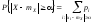 , (7.1)
, (7.1)
где
запись
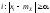 под знаком суммы означает, что суммирование
распространяется на все значения
под знаком суммы означает, что суммирование
распространяется на все значения ,
для которых точки
,
для которых точки лежат вне отрезка
лежат вне отрезка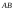 .
.
По определению дисперсия дискретной случайной величины
 .
.
Так
как все члены суммы неотрицательны, то
эта сумма только уменьшится, если
распространить суммирование не на все
значения
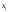 ,
а только на те, что лежат вне отрезка
,
а только на те, что лежат вне отрезка :
:
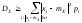 .
.
Так
как
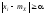 ,
то при замене под знаком суммы величины
,
то при замене под знаком суммы величины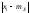 на
на ,
значение этой суммы еще больше уменьшится,
и будем иметь неравенство
,
значение этой суммы еще больше уменьшится,
и будем иметь неравенство
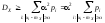 .
.
Стоящая
в правой части сумма есть не что иное,
как вероятность непопадания случайной
величины
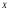 на отрезок
на отрезок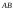 (см. выражение 7.1), и поэтому
(см. выражение 7.1), и поэтому
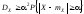 ,
,
откуда окончательно получаем
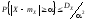 ;
;
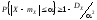 .
.
Как
и всякий общий результат, не использующий
данные о конкретном виде распределения
случайной величины
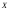 ,
неравенство Чебышева дает лишьгрубую
оценку сверху
для вероятности события
,
неравенство Чебышева дает лишьгрубую
оценку сверху
для вероятности события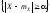 .
Если оценивать вероятность события
.
Если оценивать вероятность события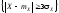 для случайной величины
для случайной величины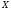 с неизвестным законом распределения,
то получим по неравенству Чебышева
с неизвестным законом распределения,
то получим по неравенству Чебышева
 .
.
Для нормального распределения эта вероятность равна 0,0027 – разница в 40 раз.
Закон больших чисел
Одной из основных задач теории вероятностей является установление закономерностей, происходящих с вероятностями, близкими к единице; при этом особую роль играют закономерности, возникающие в результате наложения большого числанезависимых или слабо зависимых факторов. Закон больших чисел устанавливает связь между средним арифметическим наблюдаемых значений случайной величины и ее математическим ожиданием и является одним из важнейших приложений теории вероятностей.
Предварительно
решим следующую задачу. Есть случайная
величина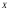 ,
имеющая математическое ожидание
,
имеющая математическое ожидание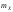 и дисперсию
и дисперсию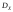 .
Над этой величиной производится
.
Над этой величиной производится независимых испытаний и вычисляется
среднее арифметическое всех наблюдаемых
значений случайной величины
независимых испытаний и вычисляется
среднее арифметическое всех наблюдаемых
значений случайной величины .
Полученное значение среднего
арифметического является случайной
величиной. Поэтому необходимо найти
числовые характеристики этого среднего
арифметического, т. е. вычислить
математическое ожидание и дисперсию,
а также выяснить, как они изменяются с
увеличением
.
Полученное значение среднего
арифметического является случайной
величиной. Поэтому необходимо найти
числовые характеристики этого среднего
арифметического, т. е. вычислить
математическое ожидание и дисперсию,
а также выяснить, как они изменяются с
увеличением .
.
В
результате опытов получена последовательность
из
 возможных значений:
возможных значений: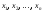 .
Удобно посмотреть на эту совокупность
чисел как на систему случайных величин
.
Удобно посмотреть на эту совокупность
чисел как на систему случайных величин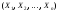 .
Очевидно, что эта система представляет
собой
.
Очевидно, что эта система представляет
собой независимых случайных величин, каждая
из которых распределена по тому же
закону, что и сама исходная величина
независимых случайных величин, каждая
из которых распределена по тому же
закону, что и сама исходная величина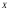 ,
т. е. выполняются следующие условия:
,
т. е. выполняются следующие условия:
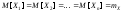 ;
;
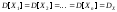 .
.
Среднее значение этих случайных величин
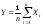 (7.2)
(7.2)
является случайной величиной с математическим ожиданием

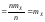 (7.3)
(7.3)
и дисперсией
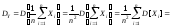
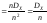 . (7.4)
. (7.4)
Получили,
что математическое ожидание случайной
величины
 не зависит от числа испытаний
не зависит от числа испытаний и равно математическому ожиданию
исследуемой случайной величины
и равно математическому ожиданию
исследуемой случайной величины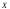 ,
а дисперсия величины
,
а дисперсия величины неограниченно убывает с увеличением
числа опытов и при достаточно большом
неограниченно убывает с увеличением
числа опытов и при достаточно большом может быть сделана сколь угодно малой.
Таким образом,среднее
арифметическое есть случайная величина
с какой угодно малой дисперсией и при
большом числе опытов ведет себя почти
как неслучайная величина.
может быть сделана сколь угодно малой.
Таким образом,среднее
арифметическое есть случайная величина
с какой угодно малой дисперсией и при
большом числе опытов ведет себя почти
как неслучайная величина.
Теорема
Чебышева. Если – последовательность
попарнонезависимых случайных
величин, имеющих конечные дисперсии,
ограниченные одной и той же постоянной
– последовательность
попарнонезависимых случайных
величин, имеющих конечные дисперсии,
ограниченные одной и той же постоянной
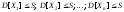 ,
,
и математические ожидания
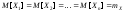 ,
,
то,
каковы бы ни были постоянные
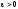 и
и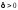 ,
,

либо
 ;
;
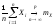 ,
,
т.
е. среднее арифметическое последовательности
независимых случайных
величин
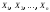 сходится по вероятности к их математическому
ожиданию.
сходится по вероятности к их математическому
ожиданию.
Доказательство. Применим для случайной величины
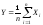 с
с
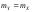 и
и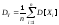
неравенство Чебышева
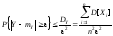 .
.
Но из условия теоремы получаем
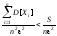 .
.
Следовательно,
каким бы малым ни было число
 ,
можно взять
,
можно взять таким большим, чтобы выполнялось
неравенство
таким большим, чтобы выполнялось
неравенство
 ,
,
где
 – сколь угодно малое число.
– сколь угодно малое число.
И тогда получаем
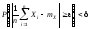 ,
,
и, переходя к противоположному событию, имеем
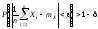 .
.
Обобщенная
теорема Чебышева.
Если законы распределения случайной
величины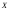 от опыта к опыту изменяются, то приходится
иметь дело со средним арифметическим
последовательности случайных величин
с различными математическими ожиданиями
и с различными дисперсиями. Для таких
случайных величин существует обобщенная
теорема Чебышева.
от опыта к опыту изменяются, то приходится
иметь дело со средним арифметическим
последовательности случайных величин
с различными математическими ожиданиями
и с различными дисперсиями. Для таких
случайных величин существует обобщенная
теорема Чебышева.
Теорема(без доказательства). Если – последовательность попарно независимых
случайных величин, имеющих конечные
дисперсии, ограниченные одной и той же
постоянной
– последовательность попарно независимых
случайных величин, имеющих конечные
дисперсии, ограниченные одной и той же
постоянной
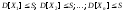 ,
,
и математические ожидания
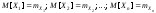 ,
,
то,
каковы бы ни были постоянные
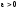 и
и ,
,

или
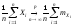 ,
,
т.
е. среднее арифметическое последовательности
независимых случайных величин
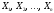 сходится по вероятности к среднему
арифметическому их математических
ожиданий.
сходится по вероятности к среднему
арифметическому их математических
ожиданий.
Теорема Маркова.Закон больших чисел может быть распространен и на зависимые случайные величины. Это обобщение принадлежит Маркову.
Теорема(без доказательства). Если имеются
зависимые случайные величины и при
и при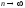
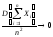 ,
,
то
среднее арифметическое наблюдаемых
значений случайных величин
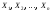 сходится по вероятности к среднему
арифметическому их математических
ожиданий:
сходится по вероятности к среднему
арифметическому их математических
ожиданий:
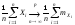 .
.
Следствия закона больших чисел
Теорема Я. Бернулли, устанавливающая связь между частотой события и его вероятностью, может быть доказана как прямое следствие закона больших чисел (теоремы Чебышева).
Теорема
Бернулли. Если производится независимых испытаний, в каждом из
которых может появиться или не появиться
некоторое событие
независимых испытаний, в каждом из
которых может появиться или не появиться
некоторое событие ,
вероятность появления которого в каждом
опыте равна
,
вероятность появления которого в каждом
опыте равна ,
то при неограниченном увеличении числа
опытов
,
то при неограниченном увеличении числа
опытов частота события
частота события сходится по вероятности к его вероятности
сходится по вероятности к его вероятности
 .
.
Обозначив
частоту события
 через
через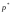 ,
теорему Бернулли можно записать в виде
,
теорему Бернулли можно записать в виде
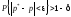 или
или
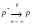 ,
,
где
 и
и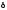 – сколь угодно малые положительные
числа.
– сколь угодно малые положительные
числа.
Доказательство.
Рассмотрим независимые случайные
величины:
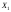 – число появлений события
– число появлений события в первом опыте;
в первом опыте;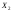 – число появленийсобытия
– число появленийсобытия
 во втором опыте; …;
во втором опыте; …; – число появлений события
– число появлений события в
в -м
опыте. Все эти случайные величины
дискретны и имеют один и тот же закон
распределения в виде индикатора событий.
Поэтому математическое ожидание каждой
из величин
-м
опыте. Все эти случайные величины
дискретны и имеют один и тот же закон
распределения в виде индикатора событий.
Поэтому математическое ожидание каждой
из величин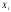 равно
равно ,
а дисперсия равна
,
а дисперсия равна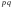 ,
где
,
где .
.
Частота
 представляет собой не что иное, как
среднее арифметическое случайных
величин
представляет собой не что иное, как
среднее арифметическое случайных
величин
 ,
,
которая,
согласно теореме Чебышева, сходится по
вероятности к общему математическому
ожиданию этих случайных величин, равному
 .
.
Теорема Бернулли утверждает свойство устойчивости частот при постоянных условиях опыта, но и при изменяющихся условиях испытаний аналогичная устойчивость также существует.
Теорема
Пуассона(следствие обобщенной
теоремы Чебышева). Если производится независимых опытов и вероятность
появления события
независимых опытов и вероятность
появления события в
в -м
опыте равна
-м
опыте равна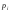 ,
то при неограниченном увеличении числа
опытов
,
то при неограниченном увеличении числа
опытов частота события
частота события сходится по вероятности к среднему
арифметическому вероятностей
сходится по вероятности к среднему
арифметическому вероятностей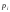 :
:
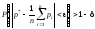 или
или
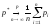 .
.
Центральная предельная теорема
Докажем центральную предельную теорему для случая одинаково распределенных случайных величин (в форме Ляпунова).
Теорема:Если
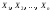 – независимые
случайные величины, имеющие одно
и то же распределение с
математическим ожиданием
– независимые
случайные величины, имеющие одно
и то же распределение с
математическим ожиданием
 и дисперсией
и дисперсией
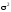 ,
то при увеличении
,
то при увеличении
 закон распределения суммы
закон распределения суммы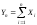 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
Доказательство.
Докажем теорему для случая непрерывных
случайных величин, применив аппарат
характеристических функций. Согласно
одному из свойств, характеристическая
функция суммы независимых случайных
величин равна произведению характеристических
функций слагаемых. Случайные величины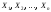 имеют одну и ту же плотность распределения
имеют одну и ту же плотность распределения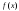 ,
а значит, и одну и ту же характеристическую
функцию
,
а значит, и одну и ту же характеристическую
функцию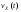 .
Не нарушая общности, можно перенести
начало отсчета всех случайных величин
.
Не нарушая общности, можно перенести
начало отсчета всех случайных величин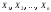 в их общее математическое ожидание
в их общее математическое ожидание ,
что равнозначно их центрированию и,
значит, тому, что математическое ожидание
каждой из них будет равно нулю.
,
что равнозначно их центрированию и,
значит, тому, что математическое ожидание
каждой из них будет равно нулю.
Для доказательства теоремы найдем характеристическую функцию гауссовой случайной величины с нулевым математическим ожиданием и единичной дисперсией, плотность распределения которой
 .
.
Характеристическая функция такой случайной величины
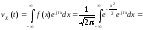
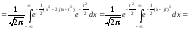
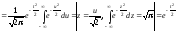 .
.
Получили,
что характеристическая функция нормальной
случайной величины
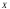 с
с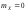 и
и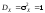 имеет вид
имеет вид
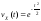 . (7.5)
. (7.5)
По
определению характеристическая функция
случайной величины
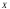
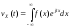 . (7.6)
. (7.6)
Характеристическая
функция случайной величины
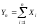 равна произведению
равна произведению характеристических функций слагаемых,
т. е.
характеристических функций слагаемых,
т. е.
 . (7.7)
. (7.7)
Разложим
 в окрестности точки
в окрестности точки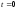 в ряд Макларена, ограничившись тремя
членами
в ряд Макларена, ограничившись тремя
членами
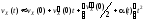 , (7.8)
, (7.8)
где
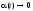 при
при .
.
Вычислим
 .
.
Так,
 по свойству нормировки функции
по свойству нормировки функции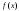 .
.
Продифференцируем
выражение (7.5) по

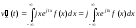 (7.9)
(7.9)
и
получаем при

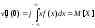 ,
,
а
так как все
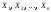 имеют одну и ту же плотность распределения
имеют одну и ту же плотность распределения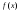 и нулевое математическое ожидание, то
и нулевое математическое ожидание, то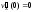 .
.
Продифференцируем
теперь (7.9):
 и соответственно при
и соответственно при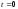 получим
получим
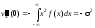 .
.
После подстановки в (7.8) имеем, что
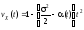 . (7.10)
. (7.10)
Для
случайной величины
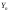 докажем, что при увеличении
докажем, что при увеличении ее закон распределения приближается к
нормальному закону распределения. Для
этого перейдем к нормированной случайной
величине
ее закон распределения приближается к
нормальному закону распределения. Для
этого перейдем к нормированной случайной
величине
 ,
,
которая
линейно связанной с
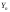 и удобна тем, что ее дисперсия равна
единице для любого
и удобна тем, что ее дисперсия равна
единице для любого .
Если докажем, что случайная величина
.
Если докажем, что случайная величина имеет нормальное распределение, то это
будет означать, что и величина
имеет нормальное распределение, то это
будет означать, что и величина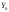 тоже распределена нормально.
тоже распределена нормально.
Докажем,
что характеристическая функция
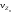 ,
однозначно определяющая плотность
распределения случайной величины
,
однозначно определяющая плотность
распределения случайной величины ,
приближается к характеристической
функции нормального закона с теми же,
что и у
,
приближается к характеристической
функции нормального закона с теми же,
что и у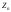 ,
параметрами:
,
параметрами: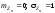 .
.
Найдем
характеристическую функцию случайной
величины
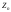 ,
используя свойства характеристических
функций и выражения (7.5) и (7.8):
,
используя свойства характеристических
функций и выражения (7.5) и (7.8):

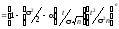 .
.
Прологарифмируем это выражение и получим
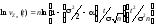 .
.
Пусть
 ,
и тогда
,
и тогда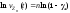 .
Если неограниченно увеличивать
.
Если неограниченно увеличивать ,
то величина
,
то величина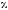 будет стремиться к нулю. Поэтому разложим
будет стремиться к нулю. Поэтому разложим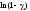 в ряд по степеням
в ряд по степеням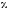 ,
ограничившись первым членом разложения,
т. е.
,
ограничившись первым членом разложения,
т. е.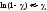 .
Таким образом, получаем
.
Таким образом, получаем
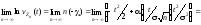
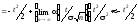 ,
,
так
как функция
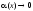 ,
когда аргумент
,
когда аргумент при
при .
.
Получили,
что
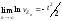 ,
следовательно,
,
следовательно,
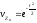 ,
,
но
это и есть характеристическая функция
нормально распределенной случайной
величины с нулевым математическим
ожиданием и единичной дисперсией (см.
выражение (7.5)). Следовательно, и линейно
связанная со случайной величиной
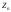 случайная величина
случайная величина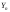 имеет
нормальное распределение.
имеет
нормальное распределение.