Методы Рунге-Кутта.

Методы Рунге-Кутта решения дифференциальных уравнений, как и метод Эйлера, принадлежат к классу одношаговых методов. Они являются своеобразным обобщением этого класса и обладают рядом достоинств:

1. обладают достаточно высокой точностью;

2. допускают использование переменного шага, что даёт возможность уменьшить его там, где значения функции быстро изменяются, и увеличить его в противном случае;

3. являются легко применимыми, так как для начала расчёта достаточно выбрать сетку х_n и задать значение y₀=f(x₀).

Наиболее часто применяют метод Рунге-Кутта четвертого порядка

Рассмотрим разложение функции (решения ДУ) в окрестности произвольной точки x_n ,

где h_n=x_n+1-x_n.

Ограничимся в разложении функции 3 первыми слагаемыми ряда, т.е.

. (*)

Тогда остаточный член в виде формы Тейлора представится в виде

или погрешность, при условии, что 3 производная ограничена на (х_n; x_n+1), имеет порядок О(h³).

Вторую производную в формуле (*) можно найти непосредственно из ДУ

y=f(x,y),

как производную от функции, заданной неявно. Получим

.

Подставив данное выражение в(*), получим

Однако такой подход не всегда приемлем, т.к. связан с отысканием частных производных функции. Чтобы избежать этого вторую производную можно представить в виде

,

где ,, – некоторые параметры.

Тогда .

Преобразуем данное выражение

(**).

Заменим приращение функции 2 переменных её дифференциалом

на

В нашем случае

.

Тогда .

и общая формула примет вид

После преобразований получим

Обозначим .

Получим

Сравнивая коэффициенты при степенях h точного решения (по формуле Тейлора) и приближённого, получим систему уравнений для определения параметров , , J, 

.

Для определения 4 неизвестных имеем систему 3 уравнений. Такая система имеет бесчисленное множество решений. Выразим через  все остальные параметры. Получим

.

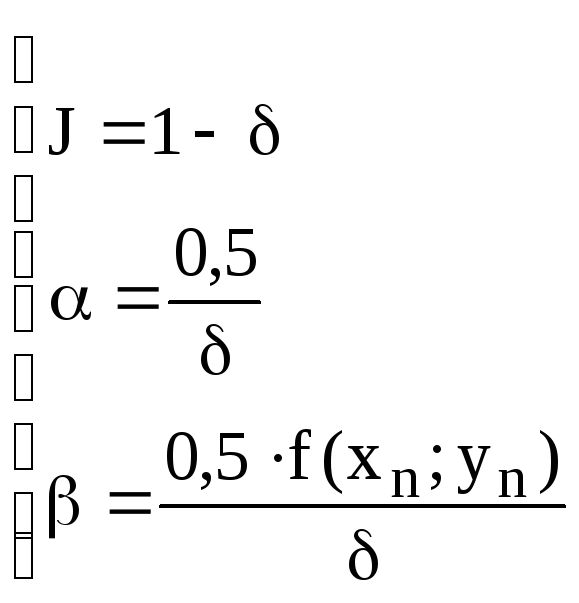Подставляя в (**) эти параметры, получим

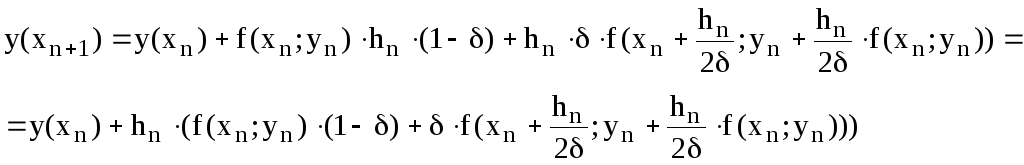
Таким образом мы получили однопараметрическое семейство схем Рунге Кутта 4 порядка точности.

Не трудно заметить, что подставляя вместо , получается формула усовершенствованного метода Эйлера.

Однако в таком виде метод Рунге- Кутта в связи с неопределённостью коэффициента  использовать не будем.

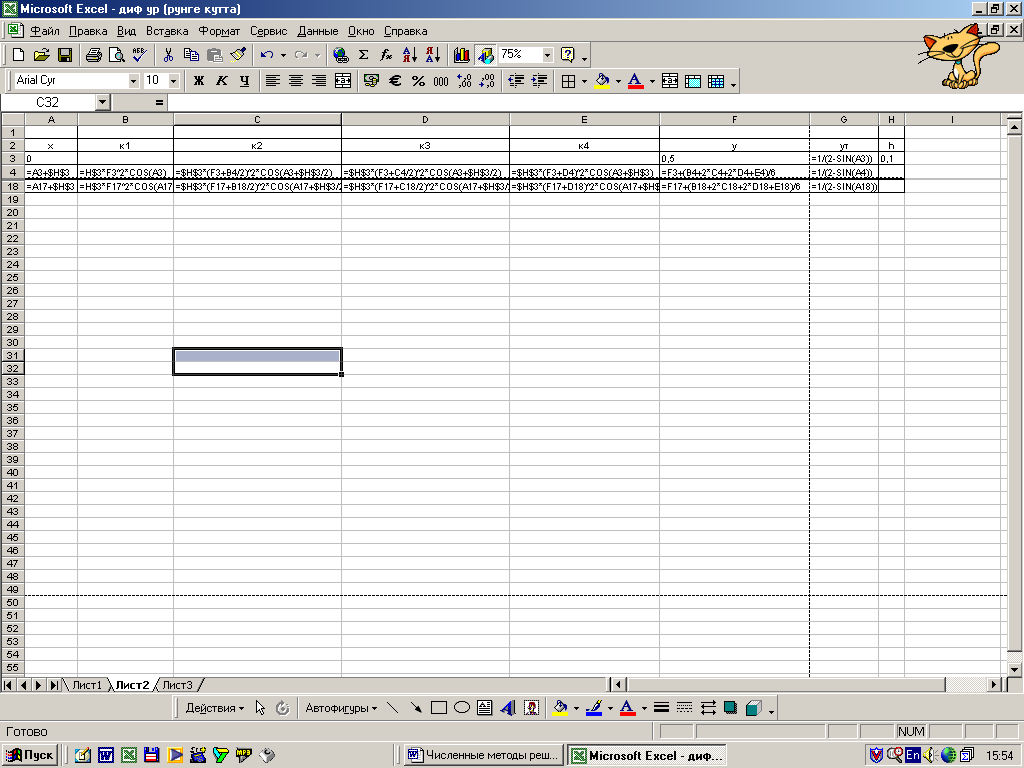
Приведем расчетные формулы метода для решения задач:

yi+1=yi+(K1+2K2+2K3+K4)/6

(4.12)

Для оценки значения производной в этом методе используется четыре вспомогательных шага на которых предварительно вычисляются величины

К1=hf(xi,yi); ; ; К4= hf(xi+h,yi+K3); i = 1, 2, 3,….. .

(4.13)

В данном методе ошибка на шаге вычислений имеет порядок h⁴.

Поскольку большинство систем ДУ и ДУ высших порядков могут быть сведены ДУ первого порядка рассмотренные методы можно применять для их решения.

Погрешность схем Рунге –Кутта. Правило Рунге.

Одним из наиболее простых, широко применяемых и достаточно эффективных методов оценки погрешности и уточнения полученных результатов в приближённых вычислениях с использованием сеток является правило Рунге.

Пусть имеется приближённая формула для вычисления величиныy(x) по значениям на равномерной сетке h_n и остаточный член этой формулы имеет вид:

Выполним теперь расчёт по той же приближённой формуле для той же точки х, но используя равномерную сетку с другим шагом rh r<1. Тогда полученное значение связано с точным значением соотношением

Заметим, что =

Тогда имея два расчёта на разных сетках, нетрудно оценить величину погрешности

.

Первое из слагаемых есть главный член погрешности. Таким образом, расчёт по второй сетке позволяет оценить погрешность расчёта по первой с точностью до членов более высокого порядка. При этом достаточная точность будет достигнута, если величина R не превышает заданной погрешности во всех совпадающих узлах. Чаще всего в качестве шагов приближённого вычисления решения уравнения выбирают h и h/2. Грубо шаг вычислений можно оценить исходя из неравенства .