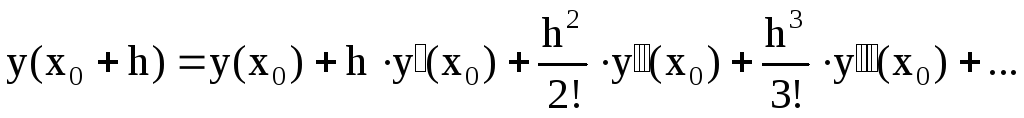Дано дифференциальное уравнение (4.3) и начальное условие

у(х0) = у0.

(4.4)

Требуется найти функцию у(х), удовлетворяющую уравнению (4.3) и начальному условию (4.4).

В отличие от задачи Коши, краевая задача ставится для дифференциальных уравнений более высоких порядков и, в частности, для уравнения второго порядка содержит два начальных условия:

у(х0) = у0, у(х1) = у1

(4.5)

Рассмотрим три основных численных метода, относящихся к классу так называемых одношаговых методов. Одношаговые методы характерны тем, что для получения очередной точки кривой у(х) требуется информация лишь о предыдущей точке.

Метод Эйлера.

Метод Эйлера обеспечивает невысокую точность решения дифференциальных уравнений. Но он весьма прост по содержанию и по реализации в электронных таблицах и математических пакетах. Кроме того, метод является основой для других, более точных методов.

Рассмотрим задачу Коши

y=f(x,y); y(x₀)=y₀.

Для перехода от уже известной точки (х₀; у₀) к точке (х₁; у₁), х₁=х₀+h, в методе Эйлера применяется следующий алгоритм.

Разложим искомую функцию у(х) в ряд в достаточно малой h окрестности точки х₀:

(4.6)

Поскольку h мало, элементами ряда, содержащими h², h³,….. можно пренебречь. Тогда из равенства получаем

у(х0+h) = y(x0)+hy(x0)

(4.7)

Т.к. y=f(x,y), то равенство (4.7) можем переписать

у(х₀+h) = y(x₀)+hf(x₀, y₀)

Мы получаем следующую точку (x_{1 ;} y₁) функции у(х).Таким образом, любая точка интегральной кривой у(х) выражается через предыдущую по формуле

уi+1 = yi + hf(xi, yi), i=0, 1, 2….

(4.8)

Такой метод решения ОДУ называется методом Эйлера. Геометрически метод Эйлера означает, что на каждом шаге мы аппроксимируем решение отрезком касательной , проведённой к графику решения в начале интервала. Точность метода невелика и имеет порядокh. Говорят, что метод Эйлера – метод первого порядка, т.е. его точность растёт линейно с уменьшением шагаh.

Пример.Рассмотрим один из вариантов оформления таблицы при решении задачи Коши методом Эйлера для уравнения

Это уравнение имеет аналитическое решение y= 1/(2 –sinx).

Поэтому у нас будет возможность оценить погрешность метода Эйлера, сравнивая полученное решение с точным.

Один из вариантов такого оформления решения задачи

a) в Excel

б) в Mathcad

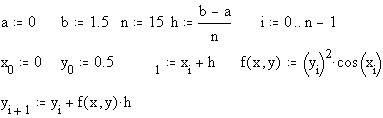
Если построить графическое решение данного ДУ и сравнить его с точным, то можно заметить, что уже при небольших значениях i ошибка у_i существенна. Поэтому метод Эйлера на практике применяют очень редко.

Модифицированный метод Эйлера.

Значительная погрешность при решении задачи Коши методом Эйлера обусловлена тем, что в разложении (4.6) удерживаются лишь два первых члена. Очевидно что, чем больше слагаемых будет удержано, тем точнее получится решение задачи Коши. Однако, чтобы сделать это, надо знать вторую и производные более высоких порядков функции у(х). Мы можем приближенно вычислить вторую производную способом конечных разностей:

(4.9)

Тогда, подставляя (4.9) в (4.6) и отбрасывая члены, содержащие h³, h⁴ и т.д., получим:

или

(4.10)

В выражении неизвестным является . Её приближённо определяют как значение функции у*(х₀ + h), вычисленной по методу Эйлера. Тогда значение функции в следующей точке примет вид:

Обобщив эту формулу, получим

(4.11)

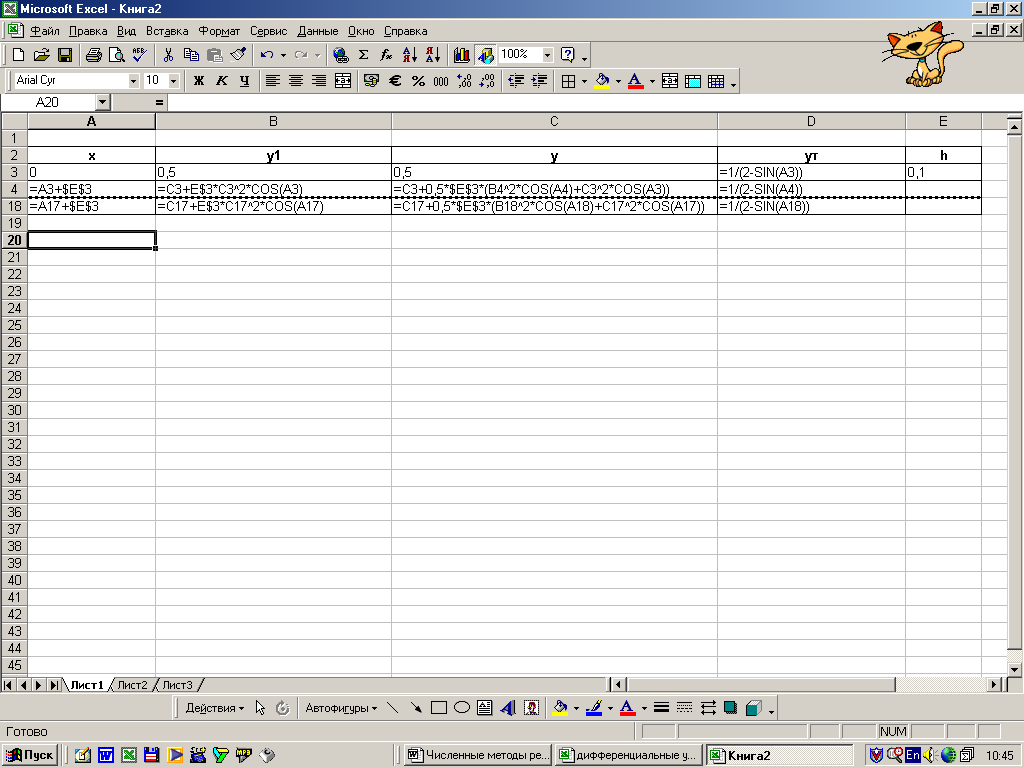
Чтобы проиллюстрировать работу модифицированного метода Эйлера, реализуем его для задачи, рассмотренной в примере 1.

а) в Excel

б) в Mathcad

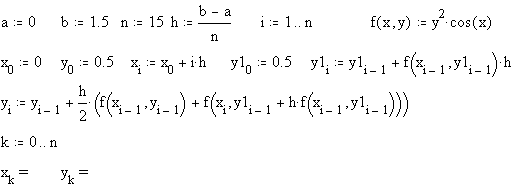
Если сравнивать результат решения задачи, полученный модифицированным методом Эйлера, с предыдущими вычислениями, то вполне очевидно преимущество модифицированного метода. Однако погрешность метода все же достаточно велика: об этом можно судить, сравнивая полученное решение с точным.