
- •Введение
- •Вывод расчетных формул
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Т а б л и ц а 2.1. Результаты измерений и вычислений
- •Контрольные вопросы
- •Лабораторная работа 3. Определение момента инерции махового колеса
- •Порядок выполнения работы
- •Контрольные вопросы
- •Порядок выполнения работы
- •Т а б л и ц а 4.1. Результаты измерений и вычислений
- •Порядок выполнения работы
- •Т а б л и ц а 5.1. Результаты измерений и вычислений
Порядок выполнения работы
1. Измерьте длину
стержня
![]() между ребрами стальных призм, на которые
опирается стержень, и геометрические
размеры сечения стержня. Полученные
данные занесите в табл. 4.1.
между ребрами стальных призм, на которые
опирается стержень, и геометрические
размеры сечения стержня. Полученные
данные занесите в табл. 4.1.
2. На середину стержня подвесьте приспособление для размещения грузов. Острие индикатора подведите под нижнюю грань стержня так, чтобы оно касалось стержня. Для этого, если требуется, переместите индикатор на нужную величину. Шкалу индикатора поверните так, чтобы в отсутствие грузов на подвеске стрелка индикатора совпадала с нулевым делением шкалы.
3. Подвесьте один
груз и определите стрелу прогиба
![]() по формуле
по формуле
= Сn1,
где С – цена малого деления индикатора (указана на шкале индика-
тора), равная 0,01 мм;
n1 – число малых делений по индикатору при нагрузке.
Сила деформации
(![]() )
равна весу грузов:
)
равна весу грузов:
![]()
где
![]() –
масса груза;
–
масса груза;
![]() –
ускорение свободного
падения.
–
ускорение свободного
падения.
Например, для груза массой 100 г (0,1 кг) имеем:
![]() =
0,1 кг
=
0,1 кг![]() 9,8
м/с2
= 0,98 Н.
9,8
м/с2
= 0,98 Н.
4. Опыт повторите два раза при той же длине стержня, но при других нагрузках.
5. Результаты измерений запишите в табл. 4.1 выразив силу деформации F в ньютонах, стрелу прогиба – в метрах.
6. Опыт повторите со стержнями другого материала и сечения (по указанию преподавателя). На основании полученных вычислений модуля упругости сделайте вывод по данной работе.
7. Модуль упругости (Юнга) вычислите по формулам (4.11), (4.12), (4.13), (4.14) в зависимости от формы сечения стержня и запишите его значение в табл. 4.1 в паскалях или в килопаскалях (1 Н/м2 = 1 Па, 1 кПа = 103 Па).
8. Найдите среднее значение модуля Юнга для каждого материала по формуле
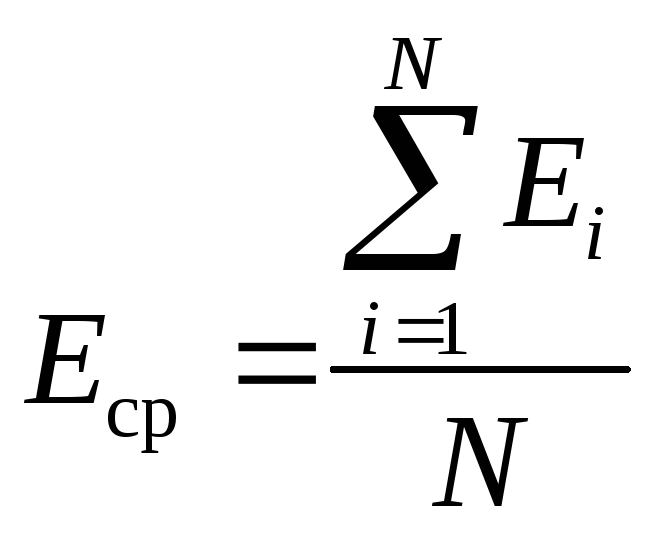 ,
,
где N – число опытов.
Отклонения от
среднего значения в каждом опыте
![]() и среднее значение отклонений
и среднее значение отклонений
 .
Результаты вычислений занесите в табл.
4.1.
.
Результаты вычислений занесите в табл.
4.1.
9. Постройте график зависимости стрелы прогиба от внешней нагрузки, откладывая по оси ОХ нагрузку F, а по оси ОY – стрелу прогиба .
Т а б л и ц а 4.1. Результаты измерений и вычислений
|
№ п.п. |
Материал стержня – |
||||||
|
Профиль стержня: l = м, а = м, b = м |
|||||||
|
F, Н |
, м |
E, Па |
Eср, Па |
Па |
Еср, Па |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
3 |
|
|
|
|
|||
Контрольные вопросы
1. Назовите виды упругих деформаций.
2. Сформулируйте закон Гука.
3. Опишите деформацию изгиба.
4. Опишите деформацию одностороннего растяжения.
5. Поясните физический смысл модуля упругости (Юнга).
6. Объясните расхождения между табличными значениями модуля упругости (приложение 1) и значениями, полученными вами в данной работе.
Лабораторная работа 5. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ
СВОБОДНОГО ПАДЕНИЯ ПРИ ПОМОЩИ
МАТЕМАТИЧЕСКОГО МАЯТНИКА МЕТОДОМ
БЕССЕЛЯ
Цель работы: определить ускорение свободного падения методом Бесселя.
Приборы и принадлежности: модель математического маятника, линейка, секундомер.
Изучите теоретический материал по одному из учебных пособий [1, гл. VI, § 45, гл. VII, § 54; 2, гл. VI, § 6.1, гл. VIII, § 8.2; 3, гл. ХIII, § 51; 4, гл. VI, § 29].
При изучении
материала необходимо четко уяснить,
что ускорение свободного падения, а
следовательно, и сила тяжести
![]() зависят от широты места. Для понимания
этой зависимости учтите, что тело массой
m,
находящееся на широте ,
участвует в суточном вращении вместе
с Землей с угловой скоростью
зависят от широты места. Для понимания
этой зависимости учтите, что тело массой
m,
находящееся на широте ,
участвует в суточном вращении вместе
с Землей с угловой скоростью
![]() (рис. 5.1). В неинерциальной системе отсчета
OXYZ,
связанной с вращающейся Землей, на любое
тело действует центробежная сила
инерции:
(рис. 5.1). В неинерциальной системе отсчета
OXYZ,
связанной с вращающейся Землей, на любое
тело действует центробежная сила
инерции:
![]() ,
,
где
![]() – центростремительное ускорение.
– центростремительное ускорение.
Величина этой силы
![]() ,
,
где
![]() –
расстояние от тела до оси вращения
Земли;
–
расстояние от тела до оси вращения
Земли;
R – радиус Земли.
Из силового
треугольника (рис. 5.1) найдите вектор
силы тяжести
![]() =
=![]() как сумму векторов силы всемирного
тяготения
как сумму векторов силы всемирного
тяготения
![]() и силы центробежной силы инерции
и силы центробежной силы инерции
![]() .
Рассмотрите частные случаи: тело
находится на экваторе (
= 0); тело находится на полюсе (
= 900).
Убедитесь, что на экваторе сила тяжести
минимальна:
.
Рассмотрите частные случаи: тело
находится на экваторе (
= 0); тело находится на полюсе (
= 900).
Убедитесь, что на экваторе сила тяжести
минимальна:
![]() ,
,
а на полюсе максимальна:
![]() .
.
Очевидно, что на других широтах
![]() .
.

Рис. 5.1.
В рассуждениях предполагалось, что Земля шарообразна. Следует также иметь в виду, что влияние вращения Земли на величину ускорения свободного падения невелико, поэтому можно полагать, что ускорение свободного падения у поверхности Земли в основном определяется силой притяжения между телом и Землей:
![]() ,
,
где G
– гравитационная
постоянная, равная 6,6![]() 10–11м3/(кг
10–11м3/(кг![]() с2);
с2);
М3 – масса Земли.
Описание лабораторной установки
и вывод расчетной формулы
Для определения ускорения свободного падения существует несколько способов. Наиболее простыми и надежными являются методы определения ускорения свободного падения с помощью математического маятника. Математическим маятником называется тело, размерами которого можно пренебречь (материальная точка), подвешенное на нерастяжимой и невесомой нити (рис. 5.2).

Рис. 5.2.
В настоящей работе используется модель математического маятника, представляющая собой металлический шарик, подвешенный на нити, длину которой можно легко изменять, перемещая вдоль линейки другой конец нити, перекинутой через блок.
Если маятник
вывести из положения равновесия на
небольшой угол (![]() ),
то возвращающая сила, действующая на
маятник, будет пропорциональна смещению,
поэтому маятник начнет совершать
гармонические колебания по закону
синуса или косинуса:
),
то возвращающая сила, действующая на
маятник, будет пропорциональна смещению,
поэтому маятник начнет совершать
гармонические колебания по закону
синуса или косинуса:
х = Аsin(t+0), (5.1)
где х – смещение тела от положения равновесия в момент времени t;
А – максимальное смещение (амплитуда);
– круговая или циклическая частота колебаний;
0 – начальная фаза.
Для получения выражения для расчета ускорения свободного падения с помощью маятника примените к нему второй закон динамики:
![]() (5.2)
(5.2)
Для этого предварительно проделайте следующее.
1. Пользуясь рис. 5.2, выразите силу f, действующую на маятник, когда он проходит произвольное положение, через силу тяжести mg и sin .
2. Принимая во внимание малость угла , выразите sin через смещение х и длину маятника l.
3. Учтите, что смещение х и сила f всегда направлены противоположно. В результате должны получить для силы выражение
![]() .
.
4. Найдите выражение для ускорения маятника по формуле
![]() ,
,
т. е. найдите вторую производную функции смещения тела из формулы (5.1).
5. Подставьте значения f и а в формулу (5.2) и произведите преобразования. В результате должны получить:
![]() .
(5.3)
.
(5.3)
6. Учитывая, что
круговая частота
связана с периодом колебаний Т
соотношением
![]() ,
из формулы (5.3) выразите g
через Т
и l.
Получите:
,
из формулы (5.3) выразите g
через Т
и l.
Получите:
![]() .
(5.4)
.
(5.4)
Из формулы (5.4) найдите
![]() .
.
Пользуясь выражением (5.4), можно определить ускорение свободного падения. Для этого достаточно опытным путем определить l и Т, но измерение l осложняется тем, что приходится определять положение точки подвеса и центра тяжести маятника. Поэтому Бесселем предложен оригинальный метод, который сводится к следующему. При произвольной длине l1 измеряется период колебаний Т1. Затем длина маятника изменяется (изменение длины определяется достаточно просто – линейкой на стене). При длине l2 соответственно определяется период колебаний Т2. В результате имеем два уравнения:
![]() ,
,
![]() .
.
Возводя эти уравнения в квадрат и произведя вычитание, получим:
![]() .
.
Отсюда
![]() ,
,
или
![]() .
(5.5)
.
(5.5)
Данное выражение является расчетной формулой для определения ускорения свободного падения методом Бесселя.
