Элементы корреляционного и регрессионного анализа

Учреждение образования «Белорусская государственная

сельскохозяйственная академия»

Кафедра высшей математики

Методические указания

по изучению темы «Элементы корреляционного и регрессионного

анализа» студентами бухгалтерского факультета заочной формы

получения образования (НИСПО)

Горки, 2013

Элементы корреляционного и регрессионного анализа

1. Основные понятия

Одной из важнейших задач математической статистики является нахождение зависимостей между переменными Х и Y. В естественных науках большей частью приходится сталкиваться с зависимостями, когда каждому значению одной величины строго соответствует определённое значение другой величины. Такие зависимости называются функциональными.

В большинстве случаев между переменными, характеризующими экономические показатели, существуют зависимости, отличные от функциональных. Зависимости между переменными, когда каждому значению переменной Х соответствует не одно, а множество возможных значений переменной Y, называются стохастическими или корреляционными. Эти зависимости обнаруживаются лишь при массовом изучении переменных.

Например, уровень производительности труда Y на предприятиях тем выше, чем больше его электровооружённость X. Вместе с тем такая зависимость может быть не обязательно однозначной. И это потому, что зависимая переменная Y испытывает влияние не только переменной Х, но и целого ряда других факторов, которые не учитываются. Кроме этого, влияние выделенного фактора может быть не прямым, а проявляться через цепочку других факторов. Поэтому в таких зависимостях каждому значению независимой переменной Х может соответствовать не одно, а ряд значений переменной Y.

При изучении корреляционных зависимостей ( связей) возникают два основных вопроса – о тесноте связи и о форме связи. Если рассматриваются только две переменные, то связь (корреляция) между ними называется парной.

Если с увеличением значений переменной Х значения переменной Y в среднем растут, то такая парная корреляция называется положительной. Если же с ростом значений переменной Х значения переменной Y в среднем уменьшаются, то такая корреляция называется отрицательной. Если же между переменными Х и Y связь отсутствует, то говорят, что имеет место нулевая корреляция.

Каждую пару значений , соответствующих значениям переменных X и Y в i-м наблюдении, можно изобразить в виде точки на координатной плоскости. Совокупность таких точек называется корреляционным полем.

2. Линейная корреляционная зависимость и прямые регрессии

Ранее было отмечено, что корреляция по направлению может быть положительной и отрицательной. Положительную корреляцию называют прямой, а отрицательную – обратной. По форме корреляция может быть линейной и криволинейной.

Парная корреляционная зависимость будет линейной, если она приближённо выражается линейной функцией.

Вид зависимости можно определить по виду корреляционного поля, т.е. по расположению построенных точек подбирается линия. Если это будет прямая, то корреляция между признаками будет линейной.

Для оценки тесноты связи между признаками используется выборочный линейный коэффициент корреляции

,

где - выборочные средние; - выборочные средние квадратические отклонения.

Так как коэффициент корреляции определяется по выборочным данным, то он является оценкой генерального коэффициента корреляции .

Коэффициент корреляции находится в пределах от -1 до 1, т.е. . Чем ближе к -1 или 1, тем теснее связь между переменными Х и Y. Чем ближе к нулю, тем слабее связь между переменными. Таким образом, по величине коэффициента корреляции можно судить о тесноте связи между двумя переменными.

По знаку коэффициента корреляции можно судить о направлении корреляционной зависимости между переменными Х и Y. Если , то зависимость прямая. Если же , то зависимость обратная.

Квадрат коэффициента корреляции называется коэффициентом детерминации и обозначается в долях или в процентах. Он показывает, на сколько процентов в среднем изменения зависимой переменной Y зависят от независимой переменной Х.

Линейная корреляционная зависимость между переменными Х и Y приближённо выражается в виде линейного уравнения

.

Это уравнение называется уравнением регрессии Y на Х, а его график называется линией регрессии. Если уравнение регрессии описывает зависимость между двумя переменными, то такая регрессия называется парной.

Парная регрессия позволяет изучить взаимосвязь лишь двух переменных. Чаще же изменение Y связано с влиянием не одного, а нескольких факторов. В этом случае в уравнение регрессии вводят несколько переменных. Такая регрессия называется множественной.

Уравнение множественной регрессии позволяет полнее объяснить поведение зависимой переменной и даёт возможность сопоставить эффективность влияния различных факторов.

Уравнение множественной регрессии с двумя независимыми переменными имеет вид .

2. Метод наименьших квадратов

Неизвестные параметры a и b уравнения регрессии находятся методом наименьших квадратов. Применяя этот метод, получим систему нормальных уравнений

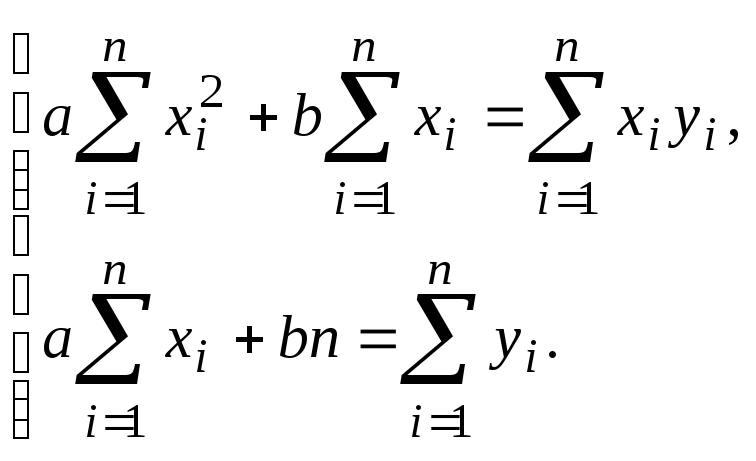
Решив систему, найдём a и b. Параметр a называется коэффициентом регрессии. Он показывает, как изменится в среднем функция Y, если аргумент Х изменится на единицу своего измерения.

Уравнение регрессии – наиболее часто встречающийся в практике вид статистической модели. Подобные модели применяются для экономического и технико-экономического анализа, где с помощью уравнений регрессии измеряют влияние отдельных факторов на зависимую переменную. Тем самым анализ становится более конкретным, а его познавательная ценность значительно увеличивается. Кроме этого, уравнения регрессии применяются при прогнозировании.

Пример. Изучается зависимость себестоимости одного изделия (Y, у.е.) от величины выпуска продукции (Х, тыс.шт.) по группе предприятий за отчётный период. Получены следующие данные:

Х	2	3	4	5	6
Y	1,9	1,7	1,8	1,6	1,4

Провести корреляционно-регрессионный анализ зависимости себестоимости одного изделия от выпуска продукции.

Решение. Построим корреляционное поле. По корреляционному полю определяем, что зависимость между себестоимостью одного изделия и выпуском продукции близка к линейной. В этом случае уравнение регрессии имеет вид .

Выполним все необходимые вычисления и запишем в виде таблицы:

№ п/п
1	2	1.9	3.8	4
2	3	1.7	5.1	9
3	4	1.8	7.2	16
4	5	1.6	8.0	25
5	6	1.4	8.4	36
Сумма	20	8.4	32.5	90

В данном примере , , , . Найдём , , , , . Вычислим выборочный коэффициент корреляции . Так как коэффициент корреляции близок к единице, то себестоимость одного изделия и объём выпускаемой продукции находятся в тесной корреляционной зависимости. Коэффициент детерминации равен , т.е. себестоимость единицы продукции на 81% зависит от объёма выпускаемой продукции и на 19% зависит от других факторов.

Для вычисления параметров a и b уравнения регрессии результаты вычислений из таблицы подставим в нормальную систему

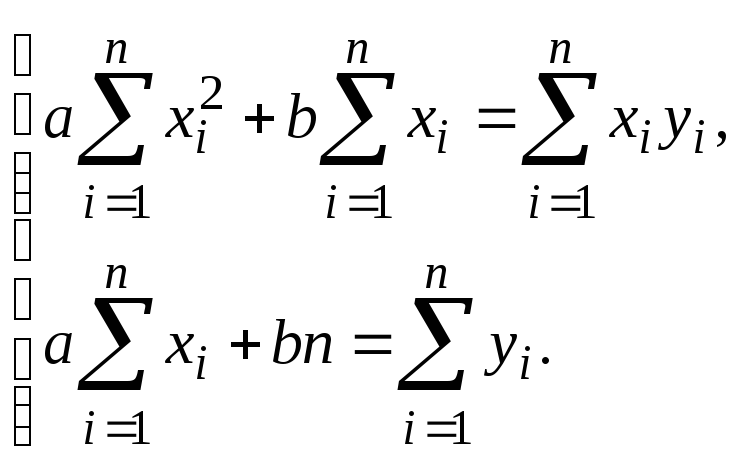
и получим систему уравнений 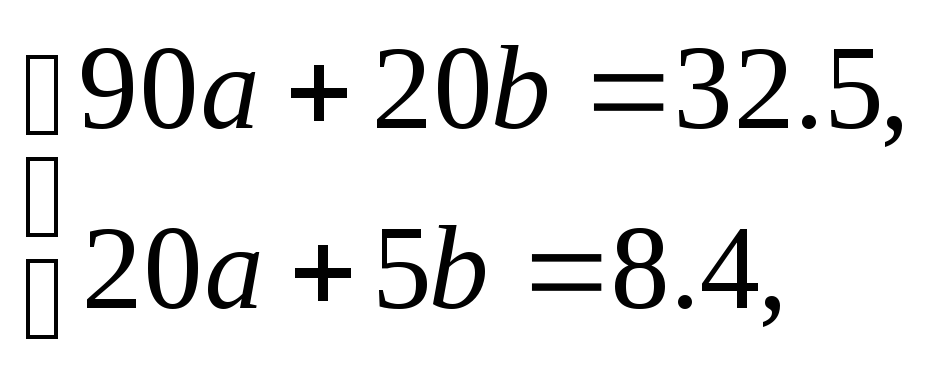из которой найдём , b=2.12. Таким образом, уравнение регрессии имеет вид . Из этого уравнения следует, что с увеличением выпуска продукции на 1 тыс. шт. себестоимость одного изделия снизится на 0.11 у.е. Если выпуск продукции составит, например, 5.2 тыс.шт., то можно определить себестоимость одного изделия: (у.е.).

Вопросы для самоконтроля знаний

1. Какие зависимости называются функциональными, а какие – стохастическими или корреляционными?

2. Когда между двумя переменными имеет место положительная, отрицательная или нулевая корреляция?

3. Что называется корреляционным полем?

4. Какой может быть корреляция по форме?

5. Для чего используется линейный коэффициент корреляции и как он определяется?

6. В каких пределах находится коэффициент корреляции?

7. Что называется коэффициентом детерминации и для чего он используется?

8. Какое уравнение называется уравнением регрессии?

9. Для чего используется метод наименьших квадратов?

9