3. Метод статистичного моделювання надійності

Метод статистичного моделювання надійності заснований на, так званому, методі Монте-Карло. Суть методу Монте-Карло полягає у використанні даних попереднього досвіду для оцінки можливих ситуацій в майбутньому. Принципова особливість методу полягає в тому, що вплив різних випадкових факторів в процесі досвіду враховується не розрахунковим, а ігровим способом. Як універсальний механізм випадкового вибору використовується сукупність випадкових чисел, рівномірно розподілених в інтервалі (0 – 1), які виробляються датчиком випадкових чисел. Випадкові числа використовуються для одержання дискретного ряду випадкових змінних, що імітують результати, які можна було б очікувати відповідно до ймовірнісного розподілу, отриманих на підставі попереднього досвіду.

Якщо ми маємо в своєму розпорядженні сукупність розподілених випадкових величин y_i (i =1, 2, …, n) в інтервалі (0 – 1), то кожній з них відповідає певне для даного виду функції F(x)=y число x_i , значення якого знаходиться зворотним перетворенням (тобто те значення аргумента x , для якого F(x) = y_i ).

Звідси слідує, що процес одержання послідовності випадкових чисел x_i із заданим законом розподілу F(x) зводиться до вирішення відносно x_i рівняння:

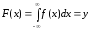(7.20)

Наприклад, якщо потрібно реалізувати випадкову величину t , розподілену за експонентним законом з відомим значенням λ

: (7.21)

Тоді, на підставі раніше наведених міркувань отримаємо

(7.22)

тоді, відповідно,

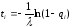(7.23)

де q_i – послідовність випадкових чисел, розподілених в інтервалі (0–1), вироблюваних датчиком випадкових чисел.

Результати моделювання являють собою статистичні середні значення величин, фіксуємі як шукані параметри:

(7.24)

де x_i – чисельне значення шуканого параметра в i -ій реалізації; N – число реалізацій алгоритму.

Відповідно до відомих граничних теорем теорії ймовірності середнє значення прагне до дійсного очікування випадкової величини при необмеженому зростанні числа випробувань.

На практиці число випробувань обмежене. В силу цього значення шуканого параметра певною мірою буде випадковим, тобто замість точного буде отримане його наближене значення, або оцінка, що має лише обмежену точність. Абсолютна величина максимального відхилення визначається в такий спосіб:

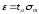(7.25)

де являє собою кількістьвеличин середньоквадратичних відхилень 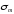для нормального закону розподілу, яку потрібно відкласти вправо і вліво від центра розсіювання, щоб ймовірність влучення на отриманий інтервал була рівною a . Значення t_a табульовані, Ф^1(a) – функція, зворотна функції Лапласа. Це означає, що кожному значенню аргументу a відповідає певна величина функції Лапласа, рівна ta .

Застосування сучасних ЕОМ дозволяє здійснити дослідження найрізноманітніших систем і при цьому імітувати реальні умови експлуатації. В цьому випадку велике значення має розробка стандартних програм і алгоритмів для вирішення типових задач надійності.

Основною характеристикою, необхідною для проведення розрахунків, є ймовірність перебування системи в певному стані P_i(t) для заданого інтервалу часу t, при якому вона здатна нормально функціонувати. В складних технічних пристроях таких станів може бути велика кількість. Для визначення конкретних станів на облік беруться всі елементи пристрою, кожний з яких може перебувати в одному із двох станів: справному або несправному.

В результаті попереднього аналізу процесу функціонування встановлюється число розглянутих станів, при яких технічний пристрій здатний функціонувати, при цьому малоймовірні ситуації звичайно виключаються.

Методика вирішення задачі оцінки надійності методом статистичного моделювання системи зводиться до наступного: заданий інтервал часу розбивається на рівні проміжки:

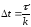(7.26)

і для кожного Δt визначається стан кожного елемента системи у відповідності з прийнятими законами розподілу часу безвідмовної роботи. Ця інформація використовується для визначення робочих станів технічних пристроїв, що відповідають деякому розглянутому проміжку часу Δt. Всі стани системи нумеруються в порядку убування показників надійності. Потім фіксується стан з найменшим номером, тобто вибирається стан системи з найкращою по надійності комбінацією справних елементів.

Аналогічно цей процес повторюється для наступного проміжку часу і так далі. Багаторазове повторення цього процесу для кожного Δt дозволяє одержати оцінку для ймовірності справного j -го стану p_j (t) в момент часу t, що належить τ.

В результаті аналізу процесу функціонування системи із множини різних M станів виділяється тільки r станів, що задовільняють вимогам нормального функціонування системи. Виходячи з цього, визначається ймовірність безвідмовної роботи системи протягом часу

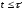
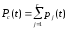(7.27)

Перевагою методу статистичного моделювання є:

- можливість не завжди використовувати аналітичні вирази, що пов'язують показники надійності технічних пристроїв і його елементів;

- простота застосування різних законів розподілу часу до відмови та часу відновлення працездатності технічних пристроїв;

- можливість використати різні способи відображення тимчасових змін значень показників надійності (гістограми, середні значення, дисперсія та інші).

В цей час метод статистичного моделювання надійності є досить популярним. В комплексі з розрахунковими методами і методами натуральних випробувань він являє собою перспективний апарат дослідження особливостей поводження і безвідмовності складних технічних пристроїв.