Методичні вказівки до виконання практичних робіт

І. До побудови лінійних регресійних моделей систем

1. Побудова лінійної регресійної моделі з одним фактором.

Розглянемо методику отримання цих моделей, загальний вигляд яких має вигляд:

y(x) = b_o + b₁·x, (1)

де b_o - вільний член;

b₁ - коефіцієнт впливу x на y (повний параметр регресії).

В завданні, що пропонується студенту, необхідно чисельно визначити значення b_o та b₁.

На координатній площині У0Х наносяться точки з координатами (х_i,y_i)

(), де N - число вибірки (розмір масивів чисел y_i та x_i). На отриманому полі, що називається кореляційним, проводиться пряма лінія y(x) таким чином, щоб відхилення y_i від цієї лінії відповідали умові:

U = [y_i – y_т(x_i)]² = min, (2)

де y_т(x_i) - значення y (теоретичні), отримані з допомогою (1) при підстановці в цю формулу x = x_i.

Особливо відмітимо, що пряма y(x) зовсім необов'язково повинна проходити через будь-яку експериментальну точку y_i, але сума квадратів відхилень y_i від y(x_i) при цьому має бути мінімальною. Якщо вираз у формулі (2) поділити на N, то отримаємо більш зрозумілу умову:

U' = [y_i – y_Т(x_i)]² = min (3)

у вигляді вимоги забезпечення мінімуму дисперсії відхилень y_i відносно лінійної математичної регресійної моделі y(x). Тому цей метод пошуку оптимального розташування y(x) на регресійному полі має назву «метод мінімізації середнього квадрату», або «метод мінімізації дисперсії відхилень», або «метод найменших квадратів» (МНК).

Щоб забезпечити умову (2), необхідно взяти похідну від U по параметрах b₀ та b₁, прирівняти її нулю. Отже:

U = 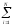[y_i - (b_o + b₁·x)]²;

звідси отримаємо наступну систему рівнянь:

(4)

Розв'язок цієї системи відносно b_о та b₁ здійснюється за допомогою правил Крамера чи Дулітла, в результаті чого отримаємо наступні формули:

(5)

Якщо помножити вираз у формулі (5) для b₁ на (-1) та поділити чисельник і знаменник на N, то можна отримати іншу форму запису цієї формули, більш зручну для користування.

(6)

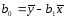
Після закінчення розрахунків b_о та b₁ проводиться перевірка гіпотези про лінійність зв'язку між y та x за допомогою коефіцієнта лінійної кореляції R - оцінка отриманої моделі на адекватність статистичним даним:

(7)

Чим ближче значення /R/ до одиниці, тим вірогідніша лінійність y(x). При цьому знак R визначається знаком коефіцієнта b₁ (якщо b₁>0, то і R > 0 і навпаки). Вважається, що лінійна модель якнайкраще описує досліджуваний процес, якщо 0,7≤R ≤1 чи -1≤R ≤-0,7.

Приклад. Математична модель, що є лінійною моделлю з двома змінними (факторами) y(x₁;x₂), має вигляд:

y = b_o + b₁·x₁ + b₂·x₂. (8)

Зробивши висновки, аналогічні для моделі y(x), можна отримати систему рівнянь відносно невідомих коефіцієнтів b_o, b₁, b₂ у вигляді:

(x'_1i)² b₁ + (x'_1ix'_2i)b₂ = (x'_1iy'_i)

(x'_2ix'_1i)b₁ + (x'_2i)² b₂ = (x'_2iy'_i) (9)

де:

x'_1iy'_i = (x_1iy_i) – N (10)

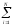(x'_1i)² = (x_1i)² – N(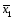)² (11)

x'_2iy'_i = (x_2iy_i) – N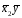 (12)

x'_1ix'_2i = (x_1ix_2i) –N (13)

(x'_2i)² = (x_2i)² – N ()² (14)

Після того, як величини, що входять в формули (10) - (14) розраховані, розв'язується система рівнянь (9) відносно b_o, b₁, b₂ за допомогою правила Крамера.

Коефіцієнт b₁ в моделі y = b_o + b₁x₁ носить назву "повний коефіцієнт регресії", який відображає вплив x₁ на y без урахування впливу x₂ на y (цей вплив враховується певним чином в значенні b₁).

Напроти, коефіцієнт b₁ в моделі y = b_o + b₁·x₁ + b₂·x₂ носить назву "частинний коефіцієнт регресії" (іноді - "чистий коефіцієнт регресії"), який відображає тільки вплив x₁ на y, виключаючи повністю вплив x₂ на y. Те ж саме стосується коефіцієнта b₂. Тому потрібно пам'ятати, що врахування найбільшої (в розумних межах) кількості змінних поліпшує точність оцінки впливу кожної з розглянутих змінних.

Аналіз отриманих моделей.

Для оцінки моделей з багатьма змінними, а також з однією змінною, застосовуються наступні показники варіації:

1. Загальна дисперсія:

(15)

2. Факторна дисперсія, що відображує вплив тільки тих змінних, які розглядаються:

(16)

3. Залишкова дисперсія (дисперсія помилок моделі):

(17)

або в більш спрощеному вигляді

(18)

Відношення

(19)

називається коефіцієнтом детермінації (у випадку лінійної множинної регресії) або індексом детермінації (у випадку нелінійної множинної регресії). Фізично він характеризує частку впливу вибраних змінних х_j в загальній варіації у.

(20)

де R – коефіцієнт множинної кореляції (або індекс кореляції для нелінійної регресії). Значення цього коефіцієнта, розрахованого за даною формулою (21), співпадає зі значенням R, розрахованим за формулою (9) для лінійної парної регресії. З урахуванням того, що , маємо ще одну розрахункову формулу:

(21)

тобто коефіцієнт кореляції розраховується по дисперсії помилок моделіі по загальній дисперсії. Розглянемо даний матеріал на конкретному прикладі.

Приклад. Визначити регресійну модель впливу капіталовкладень в розвиток виробництва (х₁), розміру основного капіталу (х₂) ті чисельності працюючих (х₃) на прибуток, який отримає підприємство після року своєї діяльності, (у). Експериментальні дані отримані в результаті огляду семи аналогічних підприємств і занесені в таблицю (N=7).

У(тис.у.о.)	620	1090	800	780	580	880	910
Х1(тис.у.о.)	10	21	15	16	11	15	19
Х2(тис.у.о.)	62	120	75	87	70	91	101
Х3(тис.у.о.)	100	170	122	138	106	140	165

Проведемо послідовний аналіз впливу:

1) капіталовкладень х₁ на прибуток у (перша модель);

2) капіталовкладень х₁ і основних фондів х₂ на прибуток у (друга модель);

3) всіх трьох змінних х₁, х_{2 і} х₃ на у (третя модель);

і прослідкуємо як при цьому змінюються параметри моделі (чисті коефіцієнти регресії) і показники точності отриманих моделей. Розрахунок виконаний ПЕОМ із застосуванням програми “MATНCAD-2”. Приведемо деякі розраховані дані:

- середньо-арифметичні значення даних величин:

Для І моделі: маємо:

тоді

Для розрахунків дисперсій визначимо за отриманою моделлю значення і для порівняння з експериментальними даними занесемо їх в таблицю:

уі	620	1090	800	780	580	880	910
	586,63	1049	796,57	838,563	628,62	736,575	964,526

Застосовуючи формули (16), (17), (19) і (20), визначимо:

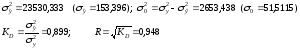
В дужках розраховані значення середньо квадратичних відхилень:

Для ІІ моделі: 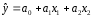маємо:

; тоді

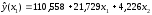
Представимо аналогічну таблицю:

уі	620	1090	800	780	580	880	910
	589,874	1074	753,461	825,904	645,904	821,079	950,258

і відповідні оцінки дисперсій та середньо квадратичних відхилень:

Оскільки _(ІІ)  _(І), а R_(ІІ) > R_(І), то можна зробити висновок, що ІІ модель більш точно описує модель в загальному вигляді.

Для ІІІ моделі: маємо:

;

тоді

Таблиця матиме вигляд:

уі	620	1090	800	780	580	880	910
	588,965	1085	761,953	824,986	649,087	813,515	936,371

Відповідні значення оцінок:

Оскільки _(ІІІ)  _(ІІ), а R_(ІІІ) > R_(ІІ), значить дана модель більш точно описує взаємозв’язки в даному об’єкті. Те, що а₃ < 0, означає неефективне використання чисельності працівників, або безпідставно збільшена заробітна плата (в межах тих даних, на яких базується даний аналіз).

2. Загальна теорія систем. Основні принципи управління в системах.

Будь-яка система управління (як технічна, так і організаційна) базується на двох основних принципах управління:

- управління по збуренню;

- управління по відхиленню.

Можлива побудова системи з використанням обох принципів одночасно, - така система є комбінованою. Кожен об'єкт управління має: змінну, якою управляють (φ); змінну, яка управляє (μ); збурення (λ).

Система управління по збуренню. Структурна схема системи, що реалізує принцип управління по збуренню має наступний вигляд:



Рис.1. Структурна схема системи управління по збуренню λ.

На рис.1 зображено: OY – об'єкт управління, що має вихідну змінну φ (наприклад, власний обсяг продажу), та дві вхідні змінні: μ – змінна, яка управляє (наприклад, ціна продажу), і λ – збурення, що впливає на φ, але не залежить від μ (наприклад, обсяг продажу конкурентів); К_р – регулятор (наприклад, регулятор ціноутворення), який змінює μ залежно від відхилення (ε) між завданням на продаж ψ та інформацією (λ_n) про збурення λ, що має місце на поточний час; компаратор ε = (ψ – λ_n), який порівнює ψ з λ_n та впливає на рішення про змінення змінної, яка керує (μ).

Коефіцієнти, що знаходяться в квадратах-блоках системи, означають відповідно:

К_λ – коефіцієнт впливу λ на λ_n, тобто λ_n = К_λ λ (якщо інформація про λ надходить без перекручень, то К_λ = 1);

К_р – коефіцієнт впливу ε на μ, тобто μ= К_р ε = К_р(ψ – λ_n);

К₁ та К₂ – відповідно коефіцієнти впливу μ та λ на φ, тобто φ= К₁μ + К₂λ.

По суті, φ = к₁μ+ к₂λ представляє собою лінійну математичну модель системи (наприклад, системи збуту автомобілів, якщо вважати К₁ = – а та К₂= – b). Враховуючи сказане вище, можна визначити залежність φ від ψ та λ таким чином:

φ= к₁μ+ к₂λ = к₁К_р(ψ – λ_n) + к₂λ = к₁К_р(ψ – К_λ·λ) + к₂λ =

= к₁К_рψ – к₁К_рК_λ·λ + к₂λ

Накінець матимемо:

φ = к₁К_рψ – (к₁К_рК_λ – к₂)λ (22)

Щоб забезпечити незалежність φ від λ, необхідне виконання умови к₁К_рК_λ – к₂ = 0, тобто К_рК_λ = к₂ / к₁. Якщо прийняти К_λ = 1 (інформація надходить без перекручень), то матимемо:

К_р =к₂ / к₁, (23)

тобто необхідну величину коефіцієнта К_р, що забезпечить незалежність φ від λ.

Таким чином, маючи модель системи збуту автомобілів, як вказано в одному з варіантів завдання, можна визначити необхідне значення коефіцієнта ціноутворення К_р, який забезпечує незалежність власного обсягу продажу від обсягу продажу конкурентів шляхом відповідної зміни вартості продажу. Студенту залишається тільки правильно визначити, чи відповідає його варіант завдання розглянутому типу системи.

Система управління по відхиленню. На відміну від попереднього типу систем управління, системи цього типу мають безпосередній зв'язок змінної, якою управляють (φ), з компаратором системи (так званий зворотній зв'язок виходу зі входом). Структурна схема систем цього типу представлена на рис.2.

-_

Позначення елементів системи прийняти ті ж, що і в попередній системі. Згідно з рис.2 зміна значення змінної μ, яка керує значенням φ, здійснюється з урахуванням відхилення ε= ψ – φ_n. Завдяки зв'язку між φ_n та φ, через коефіцієнт впливу К_оз, система діє таким чином, щоб величина відхилення ε була мінімальною навіть тоді, коли має місце значне збурення λ. Відмітимо, що в першому завданні цієї самостійної роботи є як системи управління по збуренню, так і системи управління по відхиленню. Якщо запропонована система збуту автомобілів відноситься до систем цього типу (тобто керує ціною збуту згідно з коливаннями обсягу власного продажу), то в такому випадку розв'язок даної задачі необхідно проводити за допомогою формул, що приводяться нижче.

Математична модель об'єкту залишається в тому ж вигляді: φ = К₁μ + К₂λ, але з урахуванням ε= ψ – φ_n; φ_n = К_оз·φ; μ= К_р·ε, будемо мати:

φ = (24)

що визначає залежність коливань φ від коливань завдання ψ та коливань збурення λ (для задачі, що пропонується в завданні, це залежність коливань обсягу продажу (V_n) від коливань завдання на продаж (ψ) та коливань обсягу продажу конкурентів (V_к). Всі ці змінні вимірюються у відсотках відхилення від сталого значення.

За допомогою формули (24) можна розрахувати коливання V_n (у відсотках) при заданих розмірах коливань V_k (у відсотках) та заданому значенні коефіцієнта регулятора ціноутворення при незмінності завдання (коли ψ = 0). Неважко продемонструвати, що коливання ціни продажу (μ) визначається за формулою:

μ = (25)

При ψ = 0 можна визначити μ при заданих λ та К_р. У випадку, коли необхідно визначити коливання відхилення ε (у нашому випадку – це складські залишки непроданих автомобілів), розрахунки слід проводити за формулою:

ε = φ – φ_п = ψ - К_озφ = (26)

Додамо наприкінці, що потрібно прийняти К_оз = 1, якщо інформація про обсяги власного продажу надходить у систему без перекручень.

3. Задача розподілу ресурсів між підприємствами.

Типова задача динамічного програмування (ДП) – розподілити ресурси між підприємствами на початку кожного року таким чином, щоб сумарний прибуток від усієї системи підприємств за певний період (Т) був максимальний.

Крок управління – перерозподіл ресурсів на початку кожного року.

Крокове управління на і-му кроці – сукупність виділених ресурсів підприємствам на і-му році.

Стратегія управління – сукупність крокових управлінь; її ефективність оцінюється показником ефективності (наприклад, отриманим прибутком).

Розподілити ресурси оптимально в кожному році неможливо без урахування майбутніх наслідків, тому процес динамічного програмування розгортається від кінця до початку, – таким чином знаходимо умовне оптимальне управління), а потім – від початку до кінця; серед умовних знаходяться вже оптимальні управління з урахуванням результатів попереднього кроку (початкові умови наступного року).

Розглянемо дану задачу дещо в спрощеному вигляді: як систему управління (розподілу) ресурсами між двома підприємствами з використанням лінійної регресійної моделі і умови “або все – або нічого”.

Задача розподілу ресурсів. Маємо два автотранспортні підприємства, що входять до деякого автотранспортного об’єднання. Розглянемо задачу розподілу ресурсів (капіталовкладення К) між цими підприємствами на період Т = 5 років з наступними коефіцієнтами, що є коефіцієнтами лінійних регресій, які в свою чергу є моделями функцій залишку ресурсів і отриманого року діяльності підприємств:

 – коефіцієнт щорічного прибутку І-го АТП;

 – коефіцієнт щорічного прибутку ІІ-го АТП;

 – коефіцієнт амортизації використання фондів І-го АТП;

 – коефіцієнт амортизації використання фондів ІІ-го АТП;

х – сума основних фондів, що розподіляється в І-е АТП;

у – сума основних фондів, що розподіляється в ІІ-е АТП;

К = х + у – капіталовкладення на весь період Т;

(х_і) = х_і – закон зменшення початкової суми вкладених ресурсів в І-е АТП;

(y_і) = у_і – закон зменшення початкової суми вкладених ресурсів в ІІ-е АТП;

_і = (х_і) + (y_і) – залишки від вкладань після кожного року поточного періоду, що не йдуть в прибуток (z_i), а перерозподіляються підприємствам на наступний рік (_і = к_і+1), де х_і + y_і = к_і (і=1,...,5) – сума капіталовкладень в обидва підприємства на кожному році періоду, що розглядається.

Оскільки х_і + y_і = к_і , то y_і = к_і – х_і – обсяг ресурсів, вкладених в ІІ-е підприємств ; тоді

_і = х_і + у_і = х_і +  (к_і – х_і) = ( – )х_і +  к_і ,

тобто залишок розраховується за формулою:

_і = (– )х_і +  к_і (27)

Відповідно розпишемо розрахункову формулу одержаних прибутків:

z_i = х_і + у_і = х_і + ( к_і – х_і) = (– )х_і + к_і,

тобто:

z_i = (– )х_і + к_і (28)

Розподілити ресурси між підприємствами таким чином, щоб отриманий прибуток був максимальний. Розглянемо три задачі з різними умовами: прибутки після кожного року діяльності підприємств відраховуються в автотранспортне об’єднання; прибутки вкладаються кожного року в подальший розвиток підприємств; змішаний тип задачі.

1. Задача розподілу ресурсів за умови відрахування отриманих прибутків в автотранспортне об’єднання після кожного року діяльності.

Задамо вхідні дані, які або розраховуються або задаються на основі статистичних даних відповідними службами головного підприємства:

 = 0,6,  = 0,7,  = 0,8,  = 0,85, Т= 5. Якщо параметри , , ,  в кожному році будуть різними, то задачі такого типу називаються задачами з неоднорідними етапами.

Сума прибутку, що отримується кожного року, надходить в автотранспортне об’єднання; залишок після останнього року даного періоду до прибутку не додається. Шукаємо умовне оптимальне управління, починаючи з 5-го року.

Функціональна модель задачі:

Етап 5.