
- •Рабочая программа
- •Пояснительная записка
- •Тематический план
- •Контрольные вопросы
- •Конспект лекций
- •Предисловие
- •Матрицы
- •Виды матриц
- •Равенство матриц
- •Линейные действия над матрицами
- •Линейная зависимость и независимость
- •Вопросы для самостоятельного контроля
- •Умножение матриц и системы линейных уравнений
- •Умножение матриц
- •Свойства умножения матриц
- •Матричная запись систем линейных алгебраических уравнений
- •Элементарные преобразования строк матрицы
- •Обратная матрица
- •Вопросы для самостоятельного контроля
- •Определители и системы линейных уравнений
- •Определители матриц второго порядка
- •Свойства определителя матриц второго порядка
- •Решение системы двух уравнений с двумя неизвестными с помощью определителей
- •Миноры и алгебраические дополнения элементов определителя
- •Определитель произвольного порядка
- •Свойства определителей произвольного порядка
- •Вопросы для самостоятельного контроля
- •Использование определителей для вычисления обратной матрицы и решения систем линейных уравнений
- •Отыскание обратной матрицы с помощью определителей
- •Матричный способ решения систем линейных алгебраических уравнений
- •Системы уравнений с параметрами
- •Вопросы для самостоятельного контроля
- •Решение систем линейных алгебраических уравнений в общем случае
- •Матричная запись произвольной системы
- •Ранг матрицы
- •Основная теорема о ранге матрицы
- •Вопросы для самостоятельного контроля
- •Раздел 11. Аналитическая геометрия
- •Координаты на прямой, плоскости и в пространстве
- •Простейшие задачи на координатной плоскости
- •Прямоугольные координаты в пространстве
- •Вопросы для самостоятельного контроля
- •Векторы и действия над ними
- •Понятие вектора
- •Скалярное, векторное и смешанное произведения векторов
- •Вопросы для самостоятельного контроля
- •Прямая на плоскости
- •Общее уравнение прямой
- •Геометрический смысл коэффициентов общего уравнения
- •Некоторые задачи с прямыми на плоскости
- •Взаимное расположение прямых на плоскости
- •Вопросы для самостоятельного контроля
- •Плоскость и прямая в пространстве
- •Общее уравнение плоскости
- •Прямая в пространстве
- •Взаимное расположение прямых и плоскостей
- •Вопросы для самостоятельного контроля
- •Линейные пространства
- •Основные понятия
- •Линейно независимые вектора и базис линейного пространства
- •Преобразование координат при переходе к новому базису
- •Подпространства и решения системы однородных линейных алгебраических уравнений
- •Линейные преобразования
- •Вопросы для самостоятельного контроля
- •Контроль знаний
- •Контрольная работа №3
- •Ответы
- •Глоссарий
- •Литература

Раздел 11. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
2.6. Координаты на прямой, плоскости и в пространстве
2.6.1. Задачи на координатной оси
Точка М с координатой x на оси OX обозначается M (x) . Расстояние d(A,B) между точками A (x1 ) и B (x2 ) координатной оси равно
d(A,B)= |
|
x2 − x1 |
|
(6.1) |
|
|
при любом расположении точек A и B на оси.
Для произвольного отрезка AB на оси абсцисс (A – начало отрезка, B – конец) любая третья точка С на оси делит отрезок AB в некотором от-
ношении λ , где λ = ± |
|
|
AC |
|
. Знак + выбирается только тогда, когда точка С на- |
|
|
|
|
|
|
||
|
|
CB |
|
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
ходится между A и B. Если С лежит на оси вне отрезка АВ, то выбирается знак – и λ становится отрицательным.
Пусть координата С равна x , а точек А и В, соответственно, x1 иx2 . Тогда
x = |
x1 + λx2 |
|
(6.2) |
|||
1+ λ |
||||||
|
|
|
||||
В частности, при λ =1 ,С делит АВ пополам и |
|
|||||
x = |
x1 + x2 |
|
(6.3) |
|||
|
||||||
2 |
|
|
|
|||
Пример 6.1. Построить на оси ОХ точки А(2), В(-3), С(0),Д(-3,5), Е(  2 ). Для построения точки А надо два раза отложить единичный отрезок направо от начала координат. Для точки В – утроить единичный отрезок и отложить результат влево от начала координат. Точка С – есть начало координат. Для построения точки D надо поделить единичный отрезок пополам и полученный отрезок отложить влево от точки В. Расстояние точки Е от начала координат равно длине диагонали квадрата с единичной стороной. Поэтому для построения точки Е надо построить единичный квадрат и его диа-
2 ). Для построения точки А надо два раза отложить единичный отрезок направо от начала координат. Для точки В – утроить единичный отрезок и отложить результат влево от начала координат. Точка С – есть начало координат. Для построения точки D надо поделить единичный отрезок пополам и полученный отрезок отложить влево от точки В. Расстояние точки Е от начала координат равно длине диагонали квадрата с единичной стороной. Поэтому для построения точки Е надо построить единичный квадрат и его диа-
гональ отложить вправо от начала координат.
Пример 6.2. Отрезок АВ пятью точками разделить на шесть равных частей. Найти координаты точки, ближайшей к точке В, если А(-4), В(2).
Пусть С(x) – искомая точка. Тогда λ = |
|
|
|
|
AC |
|
|
|
= 5 . Следовательно, по фор- |
||||
|
|
|
|
|
|||||||||
|
|
|
|
CB |
|
|
|
||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
муле (2) находим x = |
−4 +5×2 |
= |
6 |
=1. |
|
|
|
|
|
|
|
|
|
|
1+5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
Пример 6.3. Точка С расположена вне отрезка АВ с А(2), В(6). Расстояние от точки С до точки А в три раза больше, чем до точки В. Определить координату точки С. Нарисовать чертеж.
Имеем λ = −  BCAC
BCAC = −3. Поэтому x = 2 1−−33×6 = −−162 =8
= −3. Поэтому x = 2 1−−33×6 = −−162 =8
59

А В С
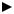 X
X
O |
|
2 |
|
6 |
|
8 |
Рис. 2.1. Иллюстрация к примеру 6.3.
Задача 6.1. |
|
Определить расстояние между точками 1) А(2) и N(-4); |
|||||||
|
|
7 |
|
|
4 |
|
; 3) A (2 5) |
|
|
2) B |
− |
|
|
и C |
− |
|
|
и B(2). |
|
|
3 |
||||||||
|
|
3 |
|
|
|
|
|
||
Задача 6.2. Убедитесь, что расстояние между точками А(x1 ) и В(x2 )можно записать в виде определителя со столбцами (1, x1 )T и (1, x2 )T .
Задача 6.3. Найти координаты середины отрезка, если его концы: 1)А(-6),
|
|
|
1 |
|
В(3); 2)А(7),С |
|
− |
|
. |
2 |
Задача 6.4. Найти точку М, симметричную точке К(-3) относительно точки Q(2). Пояснить результат чертежом.
Задача 6.5. Отрезок АВ тремя точками разделить на четыре равные части. Определить координаты всех точек деления , если А(-3), В(5).
Задача 6.6. Точка В находится правее точки А, а С – вне отрезка АВ. Убедитесь, что для всех точек С справа от В значение λ >1, а для всех точек
С слева от В верно λ <1.
Задача 6.7. Даны точки А(-7) и В(-5). Вне отрезка АВ расположены точки С и D, причем CA = BD = 3 AB . Найти координаты точек C и D.
2.6.2. Простейшие задачи на координатной плоскости
Пусть на плоскости задана прямоугольная система координат XOY. Тогда точка M этой плоскости с координатами x и y обозначается M (x, y) .
Расстояние d (M1 , M 2 ) между точками |
M1 (x1 , y1 ) и |
M 2 (x2 , y2 ) вычисляется |
|
по формуле: |
|
|
|
d (M1 , M 2 ) = |
(x2 − x1 )2 +( y2 − y1 )2 |
(6.2.1) |
|
В частности, расстояние точки M (x, y) |
от начала координат определяет- |
||
ся по формуле: |
|
|
|
d (M ,O) = d = |
x2 + y 2 |
|
(6.2.2) |
Пусть A(x1 , y1 ) и B(x2 , y2 ) – концы отрезка AB. Тогда координаты точки
С(x, y) , которая делит отрезок AB в отношении λ = ± CBAC , определяются ра-
венствами:
x = |
x1 + λx2 |
, |
y = |
y1 + λy2 |
(6.2.3) |
1 + λ |
1 + λ |
||||
|
|
|
60 |
|
|
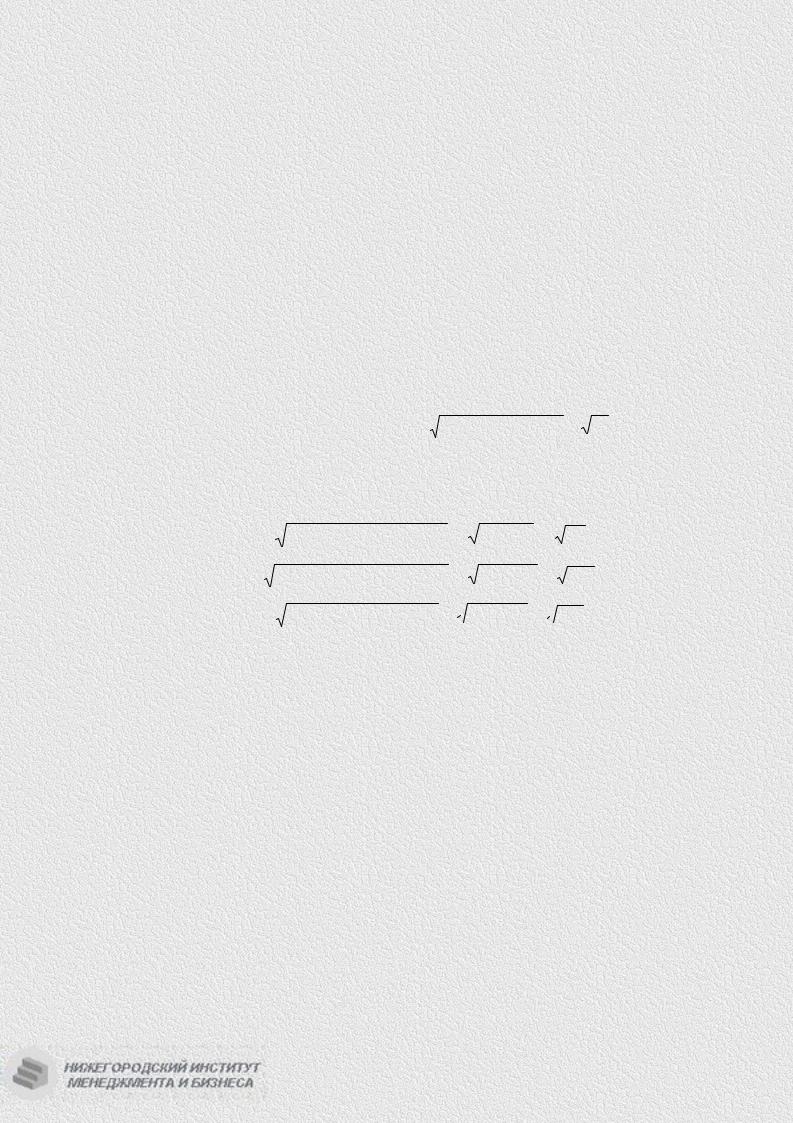
В частности, для середины отрезка AB получаем:
x = |
x1 + x2 |
, y = |
y1 + y2 |
|
(6.2.4) |
||||||||||
|
|
||||||||||||||
|
|
|
|
2 |
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|||||
Площадь треугольника с вершинами A(x1 , y1 ) , |
B(x2 , y2 ) и C(x3 , y3 ) вычис- |
||||||||||||||
ляется по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
1 |
1 |
1 |
|
|
|
|||||
|
|
|
|
|
|
||||||||||
S = |
|
|
x1 |
x2 |
|
x3 |
|
(6.2.5) |
|||||||
|
|||||||||||||||
2 |
|
|
y |
y |
2 |
|
y |
3 |
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
При этом величина площади |
|
S |
|
получается после перестановки местами |
|||||||||||
|
|
||||||||||||||
любых двух столбцов определителя, что соответствует изменению направлению обхода вершин треугольника.
Пример 6.4. Построить на координатной плоскости точки A(−2;5) , B(−2;3) и определить расстояние между точками А и В.
По формуле (6.2.1) получаем d (A, B) = (−2 + 2)2 |
+ (5 −3)2 |
= 22 = 2 . |
|||||
Пример 6.5. Показать, что треугольник с вершинами A(-5;-5), B(-3;1) и |
|||||||
C(9;-3) – прямоугольный. |
|
|
|
|
|
|
|
Для длин сторон треугольника имеем: |
|
|
|
|
|
||
d(AB) = |
(−3 +5)2 |
+ (1 −(−5))2 |
= |
22 |
+ 62 |
= |
40 |
d (AC) = |
(9 − (−5))2 |
+ (−3 − (−5))2 |
= |
142 |
+ 22 |
= |
200 |
d (BC) = (9 − (−3))2 + (−3 −1)2 =  122 + 42 =
122 + 42 =  160
160
Поскольку AB2 = 40 , AC 2 = 200 , BC 2 =160 , выполняется AC 2 = AB2 + BC 2 . Такое равенство справедливо только для прямоугольных треугольников (теорема Пифагора). Следовательно, АС – гипотенуза, АВ и ВС – катеты прямоугольного треугольника.
Пример 6.6. Найти координаты точки С, которая находится внутри отрезка АВ и отстоит от точки А (-4;3) в два раза дальше, чем от точки В (2;15).
|
Так как |
|
AC |
|
= 2 |
|
CB |
|
, то λ = |
|
|
AC |
= 2 . Здесь |
x1 = −4 , y1 = 3 , x2 = 2 , y2 |
=15 . По- |
||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
CB |
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
этому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
xc = x = − 4 + 2 × 2 = 0 , yc = y = |
3 + 2 ×15 |
=11 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 + 2 |
|
|
1 + 2 |
|
|
||||||||||||||
|
Следовательно С (0;11). |
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пример 6.7. Точка С(3;4) является серединой отрезка АВ, причем В(9;7). |
||||||||||||||||||||
Найти |
координаты точки А. |
|
|
Здесь x = 3 , |
y = 4 , x1 = 9 , y1 = 7 . |
Поэтому |
|||||||||||||||
3 = |
9 + x |
, 4 = |
7 + y |
, откуда x = −3 , |
|
|
y =1. Следовательно А (-3;1). |
|
|||||||||||||
2 |
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
61
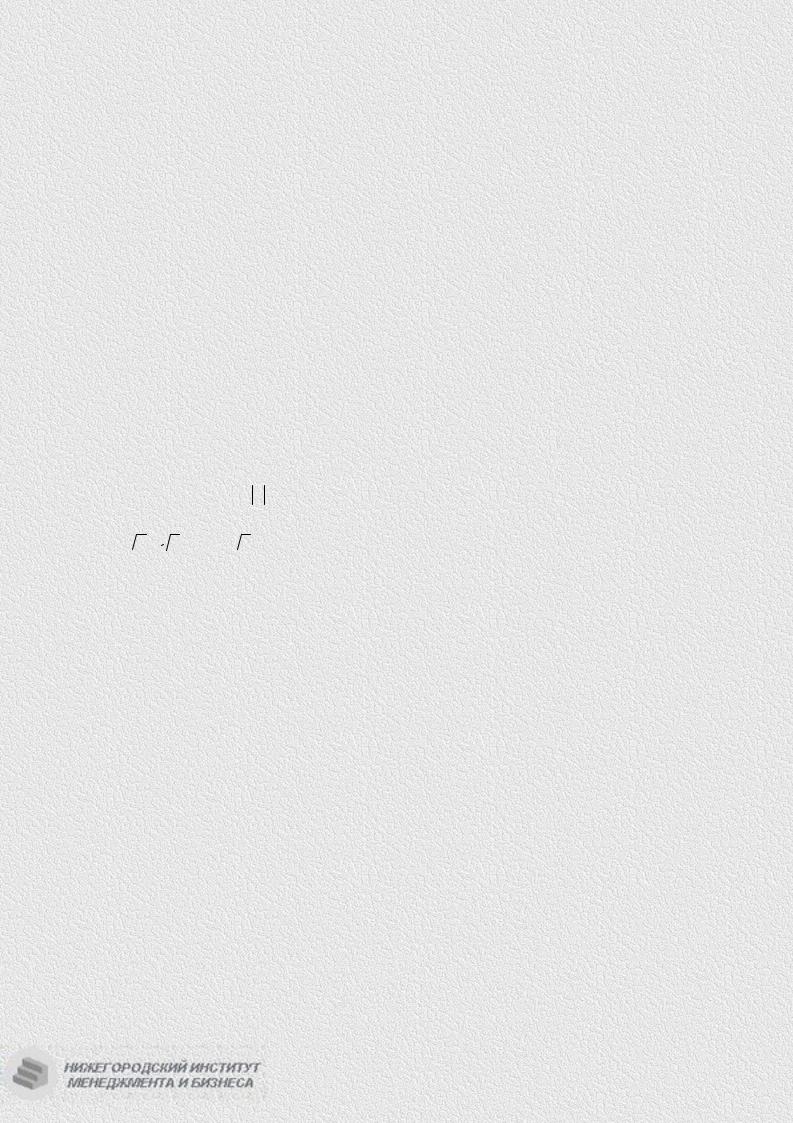
Пример 6.8. Даны вершины треугольника A(x1 , y1 ) , B(x2 , y2 ) и C(x3 , y3 ) . Найти координаты точки пересечения медиан треугольника АВС.
|
Пусть D – середина стороны АВ. Тогда ее координаты |
xD = |
x1 + x2 |
, |
||
|
2 |
|||||
|
|
y1 + y2 |
|
|
|
|
yD = |
|
. |
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
||
Известно, что точка пересечения медиан треугольника делит медиану CD в отношении 2:1, считая от точки С. Следовательно, координаты точки М пересечения медиан определяются по формулам:
x = xM |
= |
x3 + 2xD |
= |
x3 + x2 + x1 |
, y = yM |
= |
y3 + 2yD |
= |
y3 + y2 + y1 |
|
|
|
|
||||||
|
1+ 2 |
3 |
|
1+ 2 |
3 |
||||
Пример 6.9. Найти площадь треугольника с вершинами А (2;0), В (6;12)
и С (14;6).
По формуле (6.2.5) получаем:
S = |
1 |
|
1 |
1 |
1 |
= |
1 |
|
1 |
0 |
0 |
= |
1 |
(+24 |
−12 ×12) |
= |
1 |
(+24 |
−144) |
= |
1 |
(−120) |
= −60 |
|
|
2 |
6 |
14 |
|
2 |
4 |
12 |
|||||||||||||||||
2 |
2 |
2 |
2 |
2 |
||||||||||||||||||||
|
|
0 |
12 |
6 |
|
|
0 |
12 |
6 |
|
|
|
|
|
|
|
|
|
Следовательно S = 60 .
Задача 6.8. Определить расстояние между точками: 1) А(7;8) и В(-5;3); 2) C( 2;−
2;− 7) и D(3
7) и D(3 2;0) .
2;0) .
Задача 6.9. Показать, что треугольник с вершинами А(4;-1), В(7;2) и С(2;7) – прямоугольный.
Задача 6.10. Даны вершины треугольника: А(1;1), В(2;-4) и С(-8;0). Найти длину медианы, проведенной из вершины А.
Задача 6.11. Доказать, что треугольник с вершинами А(-1;-1), В(1;2) и С(2;1) – равнобедренный.
Задача 6.12. Отрезок АВ с концами А(-3;2) и В(5;6) разделен на четыре равные части. Определить координаты точек деления.
Задача 6.13. Найти площадь треугольника с вершинами А(1;3), В(2;5) и
С(4;9).
Задача 6.14. Даны две вершины треугольника: А(3;8) и В(10;2) и точка пересечения медиан М(1;1). Найти координаты третьей вершины треугольника.
Задача 6.15. Даны три последовательные вершины параллелограмма: А(10;4), В(-2;-1), С(4;7). Определить координаты четвертой вершины.
Задача 6.16. Даны вершины треугольника: А(8;3), В(2;10) и С(-7;-10). Найти расстояния точки пересечения медиан М от вершин треугольника.
Задача 6.17. Точки D(0;0), E(6;0) и F(0;8) являются серединами сторон треугольника. Вычислить площадь треугольника.
Задача 6.18. Найти периметр треугольника АВС, если А(-2;-3), В(3;-3) и
С(-2;12).
62
