4. Показательное (экспоненциальное) распределение

Определение. Непрерывная случайная величина , плотность распределения которой задается формулой

называется показательной или экспоненциальной с параметром .

График плотности вероятности равномерно распределенной случайной величины изображен на рисунке 1

Рис. 1.

В большом числе случаев показательное распределение описывает время безотказной работы прибора, при этом число интерпретируется как интенсивность отказа. Это распределение находит также широкое применение в демографии.

Свойства показательного распределения

Свойство 1. Интегральная функция распределения показательной случайной величины записывается в виде

.

Доказательство. Для того, что бы найти интегральную функцию распределения показательной случайной величины, воспользуемся свойством 3 дифференциальной функции распределения

.

Рассмотрим следующие два случая:

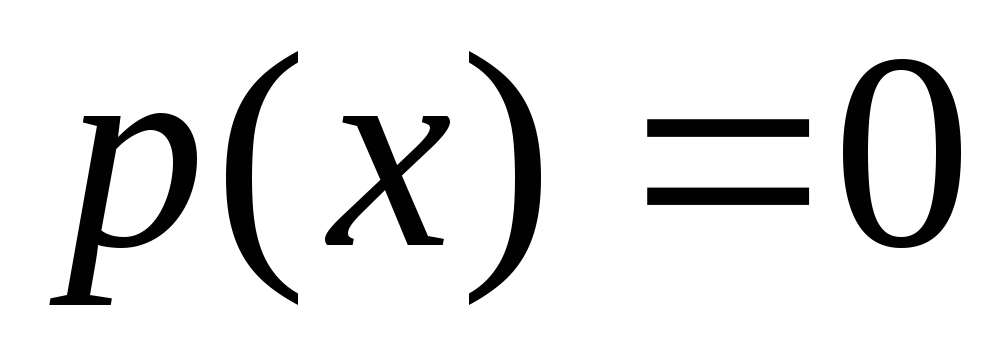1. Если , топри. Поэтому

.

2. Если , то из свойства аддитивности определенного интеграла получаем

.

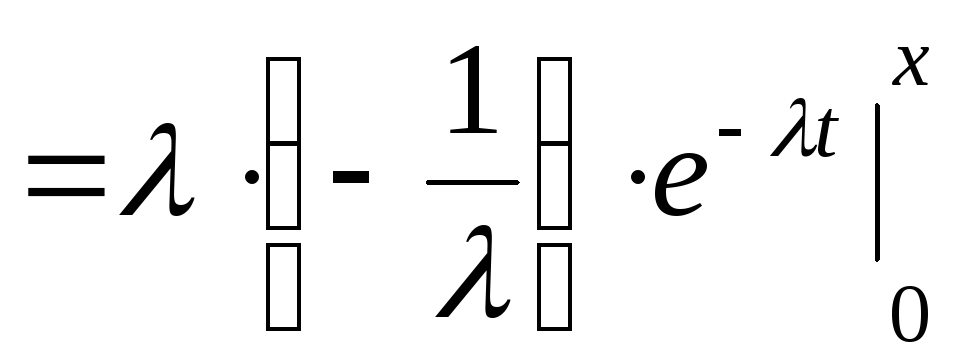
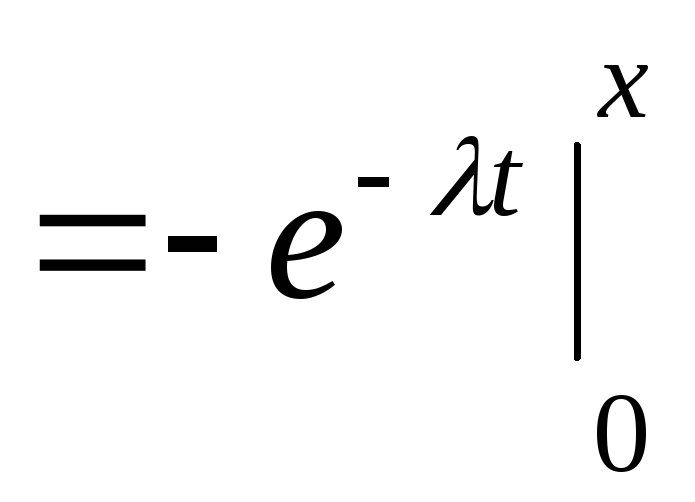
Из рассмотренных случаев следует, что интегральная функция показательно распределенной случайной величины записывается в виде

График интегральной функции показательно распределенной случайной величины изображен на рисунке 2

1

Рис. 2.

Свойство 2. Математическое ожидание случайной показательной случайной величины определяется по формуле

.

Доказательство.

.

Свойство 3. Дисперсия случайной величины показательной случайной величины определяется по формуле

.

Доказательство. Воспользовавшись формулой для вычисления дисперсии непрерывной случайной величины

,

находим

Свойство 4. Среднее квадратическое отклонение случайной величины показательной случайной величины вычисляется по формуле

.

Доказательство. Так как среднее квадратическое отклонение

,

то среднее квадратическое отклонение для равномерно распределенной случайной величины находим

Пример.

5. Нормальный закон распределения.

Нормальный закон распределения наиболее часто встречается на практике, Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Определение. Непрерывная случайная величина имеет нормальный закон распределения или закон распределения Гаусса с параметрами и, если ее плотность распределения вероятности имеет вид

.

Кривую нормального закона распределения называют нормальной или гауссовой кривой.

Выясним прежде всего теоретико-вероятностный смысл параметров нормального закона распределения.

Теорема. Если случайная величина распределена по нормальному закону, то

1) математическое ожидание случайной величины равно параметруэтого закона, т.е.

,

2) средне квадратическое отклонение случайной величины равно параметруэтого закона, т.е.

.

Доказательство.

Для того чтобы определить вид нормальной кривой, проведем исследование дифференциальной функции распределения.