Задачи по Физике

11

Относительное продольное растяжение (сжатие) :ll ,

где l – изменение длины тела при растяжении (сжатии); l – длина тела до деформации.

Относительное поперечное растяжение (сжатие) :dd ,

где d – изменение диаметра стержня при растяжении (сжатии); d – диаметр стержня.

Связь между относительным поперечным (растяжением) сжатием и

относительным продольным растяжением (сжатием) ε –,

где µ – коэффициент Пуассона.

Закон Гука для продольного растяжения (сжатия) :E ,

где Е – модуль Юнга.

Напряжение упругой деформации – Fs ,

где F – растягивающая (сжимающая) сила; s – площадь поперечного сечения. Потенциальная энергия упругорастянутого (сжатого) стержня –

O

где V – объём тела.

Механические колебания

Уравнение гармонических колебаний – x Acos t ,

где x – смещение колеблющейся точки от положения равновесия; A, ω, φ – соответственно амплитуда, круговая (циклическая) частота, начальная фаза колебаний; t – время; t – фаза колебаний в момент t.

Круговая частота колебаний – 2 , или 2 ,

где и T – частота и период колебаний.

Скорость точки, совершающей гармонические колебания, –

.

v x A sin t .

Ускорение при гармоническом колебании –

..

a x A 2 cos t .

12

Амплитуда А результирующего колебания, полученного при сложении двух, происходящих вдоль одной прямой, колебаний с одинаковыми частотами, определяется по формуле

2 12 22 2 1 2 cos 2 1 ,

где 1 и 2 – амплитуды составляющих колебаний; 1 и 2 – их начальные

фазы.

Начальная фаза φ результирующего колебания может быть найдена из формулы

tg 1 sin 1 2 sin 2 .1 cos 1 2 cos 2

Частота биений колебаний, возникающих при сложении двух колебаний, происходящих вдоль одной прямой с различными, но близкими по значению

частотами 1 и 2 , –

б 1 2 .

Уравнение траектории точки, участвующей в двух взаимно перпендикулярных

т.е. точка движется по эллипсу.

Дифференциальное уравнение гармонических колебаний материальной точки

Полная энергия материальной точки, совершающей гармонические колебания,

–

12 m 2 02 12 k 2 .

Период колебаний тела, подвешенного на пружине (пружинный маятник), –

2 mk ,

где m – масса тела; k – жёсткость пружины. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).

Период колебаний математического маятника

2 g ,

где – длина маятника; g – ускорение свободного падения.

13

где L J – приведённая длина физического маятника; J – момент инерции ma

колеблющегося тела относительно оси колебаний; a – расстояние от центра масс маятника до оси колебаний.

Эти формулы являются точными для случая бесконечно малых амплитуд. При конечных значениях они дают лишь приближенные результаты. При амплитудах не более ~ 30 погрешность в значении периода не превышает 1%.

Период крутильных колебаний тела, подвешенного на упругой нити, –

2 kJ ,

где J – момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.

Дифференциальное уравнение затухающих колебаний :

где r – коэффициент сопротивления; δ – коэффициент затухания, 2rm ;

0 - собственная круговая частота колебаний, 02 mk .

Решение дифференциального уравнения затухающих колебаний – x A(t) cos( t 0 ) ,

где А(t) – амплитуда затухающих колебаний в момент времени t; - круговая частота затухающих колебаний в момент t.

Круговая частота затухающих колебаний – 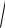0 2 2

Зависимость амплитуды затухающих колебаний от времени – t 0e t ,

где A(t) и A(t+T) – амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.

Дифференциальное уравнение вынужденных колебаний :

14

где F0 cos t – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F0 – её

Молекулярная физика

Количество вещества (молей) однородного газа находится так:

где N – число молекул газа; NA – постоянная Авогадро; m – масса газа; М – молярная масса газа.

Если система представляет собой смесь нескольких газов, то количество вещества системы равно

где n, Nn, mn, Mn – соответственно количество вещества, число молекул, масса, молярная масса n-го компонента смеси.

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона):

Законы, описывающие состояние газов на основании опытов и являющиеся частными случаями уравнения Менделеева-Клапейрона, для изопроцессов таковы:

а) закон Бойля-Мариотта (изотермический процесс: Т=const, m=const): рV=const, или для двух состояний газа p1V1=p2V2;

15

б) закон Гей-Люссака (изобарный процесс: p=const, m=const): VT const, или

для двух состояний V1 V2 ; T1 T2

состоянии; р2, V2, Т2 – те же величины в конечном состоянии.

Закон Дальтона определяет давление смеси газов: р=р1+р2+…+рn, где рn – парциальные давления компонентов смеси; n – число компонентов смеси. Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он находился в сосуде, занятом смесью.

Молярная масса смеси газов:

М m1 m2 ... mn ,

1 2 ... n

где mn – масса n-го компонента смеси; n m n – количество вещества n-го

M n

компонента смеси; n – число компонентов смеси.

Массовая доля n n-го компонента смеси газа в долях единицы или процентах находится так:

где N – число молекул, содержащихся в данной системе; – плотность вещества; V – объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов: р 23 n n ,

где n – средняя кинетическая энергия поступательного движения молекулы. Средняя кинетическая энергия поступательного движения молекулы:

n 32 kT ,

где k – постоянная Больцмана.

17

Работа расширения газа:

процессе), где Cp – показатель адиабаты.

C v

Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:

Термический кпд цикла:

Q1 Q2 , Q1

где Q1 – теплота, полученная рабочим телом от теплоотдатчика; Q2 – теплота, переданная рабочим телом теплоприемнику.

где Т1 и Т2 – термодинамические температуры теплоотдатчика и теплоприемника.

B dQ

Изменение энтропии – s A T ,

где А и В – пределы интегрирования, соответствующие начальному и конечному состояниям системы. Так как процесс равновесный, то интегрирование не зависит от формы пути.

Формула Больцмана:

s k ln W ,

где s – энтропия системы; W – термодинамическая вероятность ее состояния; k – постоянная Больцмана.

18

Электростатика. Постоянный ток.

Закон Кулона:

где F – сила взаимодействия двух точечных зарядов q1 и q2; r – расстояние между зарядами; - диэлектрическая проницаемость среды; 0 - электрическая постоянная

Закон сохранения заряда:

n

qi const,

i 1

n

где q i – алгебраическая сумма зарядов, входящих в изолированную систему;

i 1

в данную точку поля; П – потенциальная энергия заряда; А∞ - работа,

поверхности; dS – площадь элемента поверхности; En – проекция вектора напряженности на нормаль; б) через плоскую поверхность, помещенную в однородное электрическое поле:

ФЕ Е Scos .

Поток вектора напряженности Е через замкнутую поверхность –

Ф Е E n dS

S

(интегрирование ведется по всей поверхности).

Теорема Остроградского-Гаусса. Поток вектора напряженности Е через любую замкнутую поверхность, охватывающую заряды q1, q2, …, qn, –

19

n

где qi – алгебраическая сумма зарядов, заключенных внутри замкнутой

i 1

поверхности; n – число зарядов.

Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –

Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей

значение вектора напряженности составляет

E E12 E 22 2E1E 2 cos ,

где - угол между векторами Е1 и Е 2 .

Напряженность поля, создаваемого бесконечно длинной и равномерно

заряженной нитью (или цилиндром) на расстоянии r от ее оси, –

Е 2 , 4 0 r

где - линейная плотность заряда.

Линейная плотность заряда есть величина, равная его отношению к длине нити

(цилиндра):

ql .

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –

где - поверхностная плотность заряда.

20

Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:

Е qS .

Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –

E .0

Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных

которое справедливо только для изотропных диэлектриков.

Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:

Пq .

Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:

Aq .

Потенциал электрического поля в бесконечности условно принят равным нулю. Потенциал электрического поля, создаваемый точечным зарядом q на расстоянии r от заряда, –

Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков: