Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Инженерно-строительный институт

Кафедра «Автомобильные дороги и городские сооружения»

Отчет по лабораторной работе решение системы линейных алгебраических уравнений (слау)

Преподаватель __________ ______________

подпись, дата инициалы, фамилия

Студент ____________ ________________ __________ _____________

номер группы номер зачетной книжки подпись, дата инициалы, фамилия

Красноярск 2012

Содержание

Содержание …………………………………………………………………..2

1. Цель и задачи лабораторной работы…………………………… ……..3

2. Решение СЛАУ матричным методом……………………………….. …3

3. Решение СЛАУ с помощью определителей (методом Крамера)… …..4

4. Решение СЛАУ методом Гаусса…………………………………..… ….6

Вывод…………………………………………………………………….……7

Список использованных источников…………………………………….…7

1 Цель и задачи лабораторной работы

Цель: Освоить несколько вычислительных методов решения системы линейных алгебраических уравнений.

Задачи:

- научиться решать СЛАУ методами Гаусса, Крамера и обратной матрицы;

- реализовать алгоритмы решения с помощью программы Excel;

- получить навыки отладки программы;

- оценить эффективность и область применения данных методов.

2. Решение слау матричным методом

Требуется решить систему линейных уравнений

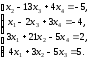(1)

Запишем систему (1) в матричном виде

. (2)

Ходрешения:

	А				Х		В
0	1	-13	4		х1		-5
1	0	-2	3		х2		-4
3	21	0	-5		х3		2
4	3	-5	0		х4		5
1. Находим определитель
det A=	2580				Функция МОПРЕД
2. Ищем обратную матрицу
-0,11047	0,09690	-0,03023	0,24845		Функция МОБР			CTRL+SHIFT+ВВОД
0,01163	0,07752	0,05581	-0,06124
-0,0814	0,12403	0,00930	-0,03798
-0,01744	0,38372	0,01628	-0,10814
3. Находим решение, умножая слева столбец В на А-1:
		Х
		1,346512			Функция МУМНОЖ				CTRL+SHIFT+ВВОД
		-0,56279
		-0,26047
		-1,95581
4. Делаем проверку - умножаем матрицу А на вектор Х слева
		-5			Функция МУМНОЖ				CTRL+SHIFT+ВВОД
		-4
		2
		5

Вывод