Электромагнетизм Основные законы и формулы

Закон Био-Савара-Лапласа:

,

где –магнитная индукция поля, создаваемого элементом проводника с током; – магнитная проницаемость; ₀ – магнитная постоянная (₀=410^-7 Гн/м); – вектор, равный по модулю длинепроводника и совпадающий по направлению с током (элемент проводника);I – сила тока; – радиус-вектор, проведенный от середины элемента проводника к точке, в которой определяется магнитная индукция.

Модуль вектора –

,

где – угол между векторами и .

Магнитная индукция связана с напряженностьюмагнитного поля соотношением

=₀,

или в вакууме

₀=₀.

Магнитная индукция в центре кругового проводника с током равна

,

где R – радиус кривизны проводника.

Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током, –

,

где r – расстояние от оси проводника до точки.

Магнитная индукция поля, создаваемого отрезком проводника, –

.

Обозначения ясны из рис. 2 а, вектор индукции перпендикулярен плоскости чертежа, направлен «к нам» и поэтому изображен точкой.

а б

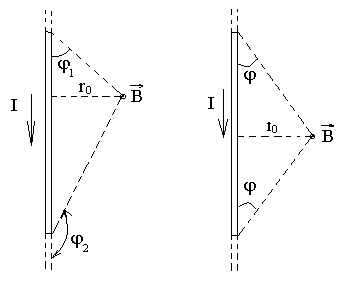
Рис. 2

При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция (рис. 2 б), -. Следовательно,

.

Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороидом на его оси), –

,

где n – число витков, приходящихся на единицу длины соленоида; I – сила тока в одном витке.

Принцип суперпозиции магнитных полей: магнитная индукция результирующего поля равна векторной сумме магнитных индукцийскладываемых полей, т.е.

.

В частном случае наложения двух полей

;

абсолютное значение вектора магнитной индукции равно

,

где  - угол между векторами .

Сила, действующая на элемент d проводника с током в магнитном поле с индукцией В (закон Ампера), –

,

где I – сила тока; – вектор, равный по модулю длине проводника и совпадающий по направлению с током;– магнитная индукция поля.

Модуль вектора определяется выражением

,

где  - угол между векторами и.

Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с током I₁ и I₂ , находящихся на расстоянии d друг от друга (с расчетом на отрезок проводника длиной ), выражается формулой

.

Вектор магнитного момента контура с током –

,

где S – площадь поверхности контура; – единичный вектор нормали к поверхности контура.

Вращающий момент сил, действующий на контур с током, помещенный в однородное магнитное поле, –

.

Модуль вращающего момента сил –

,

где  – угол между векторами и.

Потенциальная (механическая) энергия контура с током в магнитном поле –

.

Сила, действующая на контур с током в магнитном поле, изменяющемся вдоль оси х, –

,

где - изменение магнитной индукции вдоль оси х, рассчитанное на единицу длины; - угол между векторами и.

Сила , действующая на заряд, движущийся со скоростьюв магнитном поле с индукцией(сила Лоренца), выражается формулой

, или ,

где  – угол, образованный вектором скорости движения частицы и вектороминдукции магнитного поля.

Закон полного тока для тока проводимости: циркуляция вектора индукции магнитного поля вдоль замкнутого контура, охватывающего ток, выражается формулой

,

где В_е – проекция вектора индукции на направление касательной к контуру, содержащему элемент;I – сила тока, охватываемого контуром.

Если контур охватывает n токов, то

,

где – алгебраическая сумма токов, охватываемых контуром.

Магнитный поток Ф через плоский контур площадью S:

,

где  – угол между вектором нормали n к плоскости контура и вектором магнитной индукции ; В_n – проекция вектора на нормальn ().

В случае неоднородного поля

.

При этом интегрирование ведется по всей площади S.

Потокосцепление, т.е. полный магнитный поток, сцепленный со всеми

витками соленоида или тороида, –

,

где Ф – магнитный поток через один виток; N – число витков соленоида или тороида.

В магнитном поле тороида, сердечник которого составлен из двух частей, изготовленных из веществ с различной проницаемостью:

а) магнитная индукция на осевой линии тороида равна

,

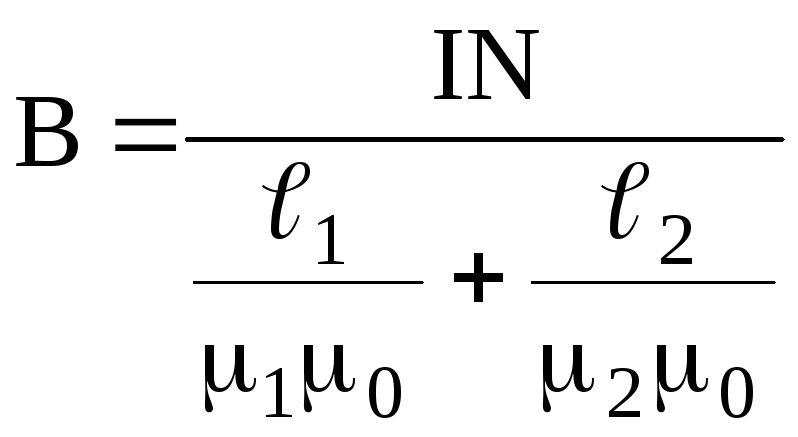где I – сила тока в обмотке тороида; N – число ее витков; ₁ и ₂ – значения длины первой и второй частей сердечника тороида; ₁ и ₂ – значения магнитной проницаемости веществ первой и второй частей сердечника тороида; ₀ – магнитная постоянная;

б) напряженность магнитного поля на осевой линии тороида в первой и второй частях сердечника составляет

; ;

в) магнитный поток в сердечнике тороида равен

,

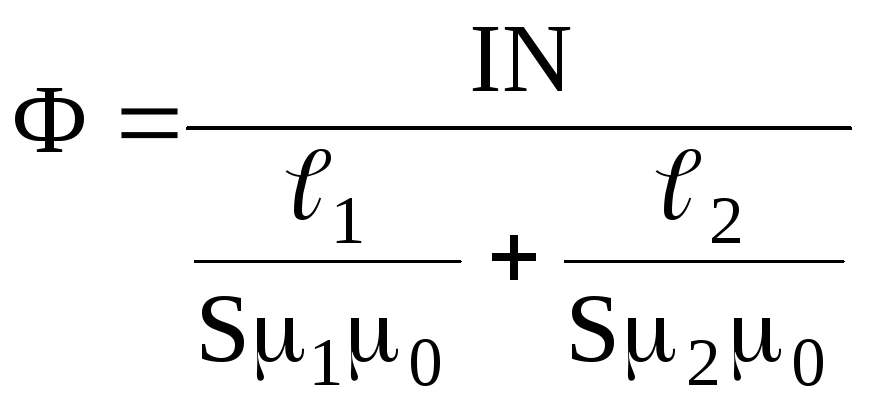или по аналогии с законом Ома (формула Гопкинсона)

,

где F_m – магнитодвижущая сила; R_m – полное магнитное сопротивление цепи;

г) магнитное сопротивление участка цепи находится по формуле

.

Магнитная проницаемость  ферромагнетика связана с магнитной индукцией В поля в нем и напряженностью Н намагничивающего поля соотноше-нием

.

Работа по перемещению замкнутого контура с током в магнитном поле равна

А=IФ,

где Ф – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; I – сила тока в контуре.

Основной закон электромагнитной индукции (закон Фарадея-Максвелла) –

,

где – электродвижущая сила индукции; N – число витков контура; – скорость изменения магнитного потока.

Частные случаи применения основного закона электромагнитной индукции:

разность потенциалов U на концах проводника длиной , движущегося со скоростьюv в однородном магнитном поле, –

,

где  - угол между направлениями векторов скорости и магнитной индук- ции;

электродвижущая сила индукции ₁ , возникающая в рамке ( число витков N, площадь – S) при ее вращении с угловой скоростью  в однородном магнитном поле с индукцией В, –

,

где t – мгновенное значение угла между вектором и вектором нормали в плоскости рамки.

Количество электричества Q, протекающего в контуре, –

,

где R – сопротивление контура;  – изменение потокосцепления.

Электродвижущая сила самоиндукции ₁ , возникающая в замкнутом контуре при изменении силы тока в нем, –

, или ,

где L – индуктивность контура.

Потокосцепление контура –

,

где L – индуктивность контура.

Индуктивность соленоида (тороида):

,

где V – объем соленоида.

Во всех случаях вычисления индуктивности соленоида (тороида) с сердечником по приведенной формуле для определения магнитной проницаемости следует пользоваться формулой

.

Мгновенное значение силы тока I в цепи, обладающей активным сопротивлением R и индуктивностью L, находится так:

после замыкания цепи – ,

где  - ЭДС источника тока; t – время, прошедшее после замыкания цепи;

после размыкания цепи – ,

где I₀ – значение силы тока в цепи при t=0; t – время, прошедшее с момента размыкания цепи.

Энергия W магнитного поля, создаваемого током в замкнутом контуре с индуктивностью L, определяется формулой

,

где I – сила тока в контуре.

Объемная плотность энергии однородного магнитного поля длинного соленоида –

.

Формула Томсона. Период собственных колебаний в контуре без активного сопротивления –

,

где L – индуктивность контура; С – его электроемкость.

Взаимосвязь длины электромагнитной волны, периода Т и частоты колебаний –

=сТ, или ,

где с – скорость электромагнитных волн в вакууме (с=310³ м/с).

Скорость электромагнитных волн в среде –

,

где  - диэлектрическая проницаемость;  - магнитная проницаемость среды.