58

ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК

Основные законы и формулы

Закон Кулона:

,

где F – сила взаимодействия двух точечных зарядов q₁ и q₂; r – расстояние между зарядами;  - диэлектрическая проницаемость среды; ₀ - электрическая постоянная

.

Закон сохранения заряда:

,

где – алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.

Напряженность и потенциал электростатического поля:

; , или,

где – сила, действующая на точечный положительный зарядq₀, помещенный в данную точку поля; П – потенциальная энергия заряда; А_∞ - работа, затраченная на перемещение заряда q₀ из данной точки поля в бесконечность.

Поток вектора напряженности электрического поля:

а) через произвольную поверхность S, помещенную в неоднородное поле:

, или ,

где  – угол между вектором напряженности и нормальюк элементу поверхности;dS – площадь элемента поверхности; E_n – проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле:

.

Поток вектора напряженности через замкнутую поверхность –

(интегрирование ведется по всей поверхности).

Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –

,

где – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.

Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –

.

Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:

внутри сферы (r R) Е=0;

на поверхности сферы (r=R) ;

вне сферы (r  R) .

Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой

.

В случае двух электрических полей с напряженностями иабсолютное значение вектора напряженности составляет

,

где  - угол между векторами и.

Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –

,

где  - линейная плотность заряда.

Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):

.

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –

,

где  - поверхностная плотность заряда.

Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:

.

Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –

.

Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.

Электрическое смещение связано с напряженностьюэлектрического поля соотношением

,

которое справедливо только для изотропных диэлектриков.

Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:

.

Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:

.

Потенциал электрического поля в бесконечности условно принят равным нулю.

Потенциал электрического поля, создаваемый точечным зарядом q на

расстоянии r от заряда, –

.

Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:

внутри сферы (r  R) ;

на поверхности сферы (r = R) ;

вне сферы (r  R) .

Во всех формулах, приведенных для потенциала заряженной сферы,  есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.

Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов , создаваемых отдельными точечными зарядами:

.

Энергия W взаимодействия системы точечных зарядов определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой

,

где - потенциал поля, создаваемый всеми (n-1) зарядами (за исключением i-го) в точке, где находится заряд .

Потенциал связан с напряженностью электрического поля соотношением

.

В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой

,

или в скалярной форме

.

В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –

,

где ₁ и ₂ – потенциалы точек двух эквипотенциальных поверхностей; d - расстояние между этими поверхностями вдоль электрической силовой линии.

Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал ₁, в другую, имеющую потенциал ₂, равна

, или ,

где E – проекция вектора на направление перемещения;- перемещение.

В случае однородного поля последняя формула принимает вид

,

где – перемещение; - угол между направлениями вектора и перемеще-ния.

Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.

Электрический момент диполя есть вектор, направленный от отрицательного заряда к положительному, равный произведению зарядана вектор, проведенный от отрицательного заряда к положительному, и называемый плечом диполя, т.е.

.

Диполь называется точечным, если его плечо намного меньше расстоянияr от центра диполя до точки, в которой нас интересует действие диполя ( r), см. рис. 1.

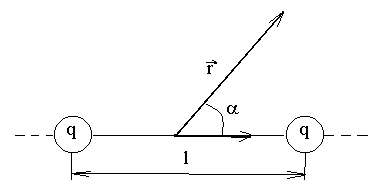
Рис. 1

Напряженность поля точечного диполя:

,

где р – электрический момент диполя; r – абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует;  - угол между радиус-вектором и плечомдиполя.

Напряженность поля точечного диполя в точке, лежащей на оси диполя

(=0), находится по формуле

;

в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , – по формуле

.

Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет

,

а в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , –

=0.

Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.

Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –

, или ,

где  - угол между направлениями векторов и.

Электроемкость уединенного проводника или конденсатора –

,

где q – заряд, сообщенный проводнику; - изменение потенциала, вызванное этим зарядом.

Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –

.

Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.

Электроемкость плоского конденсатора:

,

где S – площадь каждой пластины конденсатора; d – расстояние между пластинами;  - диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной d_i и диэлектрической проницаемостью _i каждый (слоистый конденсатор), составляет

.

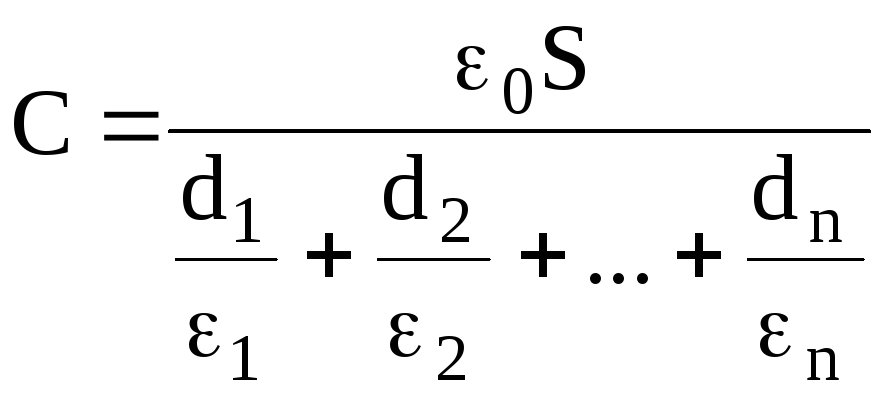Электроемкость сферического конденсатора (две концентрические сферы радиусом R₁ и R₂ , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:

.

Электроемкость последовательно соединенных конденсаторов составляет:

в общем случае –

,

где n – число конденсаторов;

в случае двух конденсаторов –

;

в случае n одинаковых конденсаторов с электроемкостью С₁ каждый –

.

Электроемкость параллельно соединенных конденсаторов определяется следующим образом:

в общем случае –

С=С₁+С₂+…+С_n;

в случае двух конденсаторов –

С= С₁+С₂;

в случае n одинаковых конденсаторов с электроемкостью С₁ каждый –

С=nС₁.

Энергия заряженного проводника выражается через заряд q, потенциал  и электроемкость С проводника следующим образом:

.

Энергия заряженного конденсатора –

,

где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.