Противоположным по отношению к событию а называется событие ā, состоящее в не появлении а и, значит, дополняющее его до ω.

Примеры

1) опыт – выстрел по мишени:

А – попадание в мишень

Ā – непопадание в мишень

2. опыт – подбрасывание игрального кубика:

А – появление четной цифры

Ā – появление нечетной цифры

2. опыт – подбрасывание монеты

А – герб

Ā – цифра

В частности, если два события А и Ā противоположны, то они образуют полную группу несовместных событий и

P(A) + P(Ā) = 1,

т.е. сумма вероятностей противоположных событий равна единице.

Это свойство противоположных событий очень широко применяется в теории вероятностей. Часто бывает проще вычислить вероятность противоположного события Ā, чем вероятность интересующего нас события А. Тогда вычисляют P(Ā), вычитают ее из единицы и находят:

P(A) = 1 – P(Ā).

Выведем еще одно следствие правила сложения. Если события а и в совместны (ав  æ), то

Р (А + В) = Р(А) + Р(В) – Р(АВ).

Докажем его. Представим событие А + В как сумму трех несовместных вариантов.

А + В = {А, но не В} + {В, но не А} + АВ =

= АB̅ + ВĀ + АВ.

По правилу сложения

Р (А + В) = Р(А B̅) + Р(ВĀ) + Р(АВ).

Но

А= АB + АВ; Р(А) = Р(А B) + Р(АВ);

В = ВĀ + АВ; Р(В) = Р(ВĀ) + Р(АВ);

откуда

Р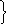(АB) = Р(А) – Р(АВ),

Р(ВĀ) = Р(В) – Р(АВ)

Подставляя это выражение, получим

Р(А + В) = Р(А) – Р(АВ) + Р(В) – Р(АВ) + Р(АВ) =

= Р(А) + Р(В) ­– Р(АВ),

что и требовалось доказать.

Условная вероятность события. Правило умножения вероятностей.

Условной вероятностью события В при наличии А называется величина

Р(В /А) = Р(АВ)/Р(А)

Условную вероятность Р(В/А) можно трактовать, как вероятность события В, вычисленную при условии (в предположении), что событие А произошло.

На практике формулу Р(В/А) = Р(АВ)/Р(А) обычно читают «в обратном порядке», для чего записывают ее в виде:

Р(АВ) = Р(А) ∙ Р(В/А)

т.е. вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого.

Сформулированное правило называют правилом умножения вероятностей.

Правило умножения вероятностей легко обобщается на случай произвольного числа событий:

Р(A₁ A₂ ... A_n) = Р(A₁) Р( A₂/A₁) Р(A₃/ A₁A₂)…Р(A_n/A₁A₂…A_{n -1}),

т.е. вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего события вычисляется при условии, что все предыдущие имели место.

Событие А называется независимым от события В, если его вероятность не зависит от того, произошло В или нет, т.е. Р(А/В) = Р(А).

В противном случае, если Р(А/В)  Р(А), событие А зависит от В.

Пример1. Опыт – два раза подбрасывается монета. Событие А - появление герба при первом бросании монеты. Событие В - появление герба при втором бросании монеты.

События независимы.

Пример 2. Опыт – выбор шара из урны с двумя белыми и одним черным шарами. Событие А - появление белого шара при первом вынимании. Событие В - появление белого шара при втором вынимании.

События зависимые.

Зависимость и независимость событий всегда взаимны: если А зависит от В, то и В зависит от А, и наоборот.

Докажем это. Пусть событие А не зависит от В:

Р(А ‌ В) = Р(А).

Запишем правило умножения в двух формах:

Р(АВ) = Р(А) ∙ Р(В/А)

Р(АВ) = Р(В) ∙ Р(А/В).

Отсюда, заменяя в последнем выражении условную вероятность Р(А/В) на «безусловную» Р(А), имеем:

Р(А)Р(В/А) = Р(В)Р(А).

Или, предполагая, что Р(А)  0, и деля обе части равенства на Р(А),

Р(В/А) = Р(В),

т.е. событие В не зависит от А, что и требовалось доказать.

В связи с этим можно дать новое определение независимых событий:

Два события называются независимыми, если появление одного из них не меняет вероятности появления другого.

Для независимых событий правило умножения вероятностей принимает особенно простой вид:

Р(АВ) = Р(А) Р(В),

т.е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Несколько событий A₁, A₂, …, A_n называются независимыми, если любое из них не зависит от любой комбинации (произведения) любого числа других. Для независимых событий правило умножения принимает вид:

Р(A₁∙ A₂∙ …∙ A_n ) = Р(A₁) ∙ Р(A₂) ∙…∙Р(A_n)

Или, короче, пользуясь знаком произведения:

= ,

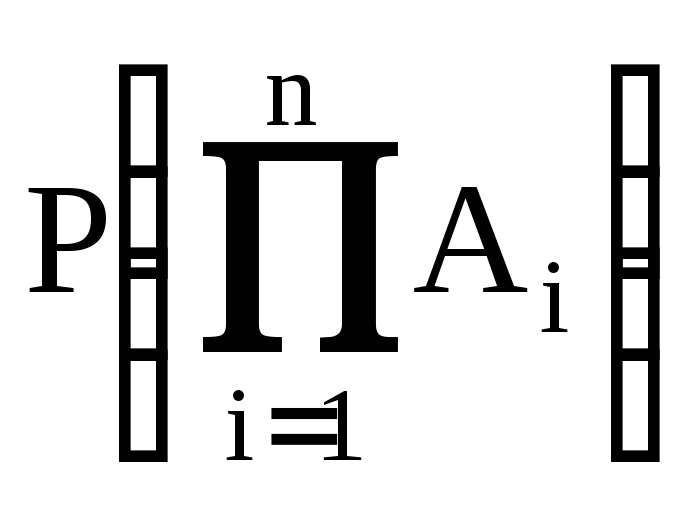т.е. вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий.

Заметим, что если имеется несколько событий

A₁, A₂, …, A_n ,

то их попарная независимость (т.е. независимость любых двух событий A_i и A_j с разными индексами) еще не означает их независимости в совокупности.

Задача. Стрелок производит 3 выстрела по одной мишени. Вероятность попадания в каждом выстреле одинакова и равна 0.9.

Найти вероятность того, что в мишени будет:

а) 0 пробоин (событие – А);

б) 1 пробоина (событие – В);

в) 2 пробоины (событие – С);

г) 3 пробоины (событие – D).

Найти Р(А); Р(В); Р(С); Р(D).

Обозначим

А₁ – попадание в 1-м выстреле

А₂ – попадание во 2-м выстреле события независимы

А₃ – попадание в 3-м выстреле

D = А₁·А₂·А₃ Р(D) = Р(А₁)·Р(А₂)·Р(А₃) = 0.9³ = 0.729

А = Ā₁ · Ā₂ · Ā₃ Р(А) = Р(Ā₁) · Р(Ā₂) · Р(Ā₃) =

= (1 – 0.9)³ = 0.001

В = А₁· Ā₂ ·Ā₃ + Ā₁ ·А₂ · Ā₃ + Ā₁ · Ā₂ ·А₃

Р(В) = 3·0.9·0.1² = 0.027

С = А₁· А₂ · Ā₃ + А₁· Ā₂ ·А₃ + Ā₁ ·А₂·А₃

Р(С) = 3·0.9²· 0.1 = 0.243

Р(А) + Р(В) + Р(С) + Р(D) =1