Метод хорд і дотичних (комбінований метод)

Розглянемо рівняння (1) і нехай у точці виконується умова. Застосуємо в цій точці метод дотичних, а в точці х₀ =а – метод хорд. Ітераційні формули комбінованого методу мають вигляд:

(7)

Геометрична інтерпретація методу. В точці проводять до­тичну до кривої та отримують наближення , а через точкитапроводять хорду й отримують набли­ження, тобто на кожному наступному кроці метод хорд застосовують до нового проміжку. Процес продовжують, доки не виконається умова <.

Коренем рівняння (1) буде .

Метод простих ітерацій

Нехай відомо, що корінь рівняння (1) лежить на відрізку .

Перетворимо рівняння (1) до вигляду

(8)

Таке перетворення може бути виконано різними способами, але для збіжності треба забезпечити виконання умови

<1 (9)

Метод простих ітерацій або метод послідовних наближень полягає у тому, що вибираємо початкове наближення кореня рівняння (8), де й обчислимо перше наближення за формулою, а далі. Наступні наближення описує формула

,(10)

Якщо існує границя ,тоє коренем рівняння (8).

Теорема 1. Нехай функція визначена та диференційована на відрізку(в області), причому всі її значення. Тоді, якщо існує правильний дрібтакий, що виконується нерівність (9) при, то:

1. процес ітерації (10) збіжний незалежно від початкового наближення ;

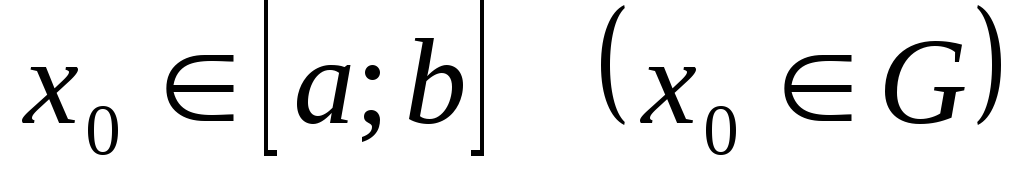2. граничне значення є коренем рівняння (8) на відрізку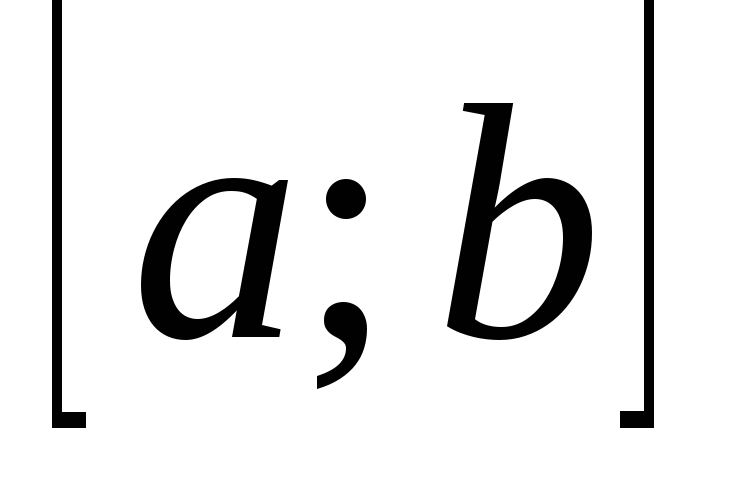

(в області ).

Зауваження 1. Теорема залишається вірною, якщо визначена і диференційована в нескінченому інтервалі, причомуповинна задовольняти (9).

Зауваження 2. В умовах теореми 1 ітерації збігаються при будь-якому виборі . Окрема похибка в обчисленнях, яка не виходить за межі проміжку, не впливає на кінцевий результат. Зростає лише об'єм обчислень. Тому це надійний метод обчислень.

Теорема 2. Нехай функція визначена і диференційована на деякому відрізку, причому рівняння (8) має корінь, який лежить у більш вузькому відрізку, де;. Тоді, якщо виконується (9) і початкове наближення, то:

1. всі послідовні наближення знаходяться в інтервалі :

2. процес послідовних наближень збіжний, тобто існує , причому- єдиний корінь на відрізкурівняння (8);

3. виконується оцінка (11).

(11)

Зауваження. Нехай в деякому околі коренярівняння (8) похідназберігає сталий знак і виконана нерівність (9). Тоді, якщо похіднадодатна, послідовні наближення (10) збігаються до коренямонотонно. Якщо похіднавід’ємна, то послідовні наближення коливаються біля кореня.

Геометрична інтерпретація Геометрична інтерпретація

методу простих ітерацій методу простих ітерацій

для випадку для випадку

Геометрична інтерпретація Геометрична інтерпретація

методу простих ітерацій методу простих ітерацій

для випадку > для випадку>1

Приклад 1. Знайти дійсні корені рівняння з точністю до трьох значущих цифр.

Запишемо . Графічним способом встановлюємо, що рівняння має на відрізкуодин дійсний корінь. Дотримуючись визначень теореми 2, задаємо:і. Звідси

.

Так як і, то примаємо:

<1.

Якщо виберемо , то всі умови теореми 2 будуть виконані. Виберемоі граничну абсолютну похибку

4 і 5 наближення збігаються з точністю до 4 знаків. Тому:

Так як гранична абсолютна похибка приблизного кореня , включаючи похибку округлення, не перевищує: 0,0005+0,0001=0,0006<0,0005, то можна прийняти.

Приклад 2. Методом простих ітерацій з точністю знайти корінь трансцендентного рівняння на відрізку.

Запишемо рівняння у вигляді: . На відрізкумаємо<1. За початкове наближення обираємо. Ітераційний процес запишемо у вигляді:

Послідовно знаходимо:

На 5 і 6 ітераціях виконується <, тому.

Звідси бачимо, що збіжність двостороння і лінійна, тому що відношення приблизно однакові прита рівні(знаменник геометричної прогресії).

Зауваження 1. Вихідне рівняння можна записати у вигляді рівності, вибираючи різним способом. У деяких випадкахбуде менший, а в інших – більший в околі шуканого кореня. Для метода простої ітерації найкращим є такий запис, для якого<1, причому для меншихшвидкість збіжності до кореняє більшою.

Зауваження 2. Можна виразити із рівняннятак, щоб для отриманого рівняння виконувалась умова збіжності<1 в околі шуканого кореня.

Зауваження 3. Загальний прийом зведення (1) до (2), для якого забезпечено виконання <1.

Нехай , причому 0<. Замінюємо (1) еквівалентним

, де >0- константа. Тоді:. Вибираємо λ, щоб в околі ξ виконувалась нерівність:<1.

Звідси на основі попереднього: Якщо,, то<1.

Приклад 3. Знайти найбільший додатній корінь рівняння(1) з точністю. Інтервал знаходження кореня. Рівняння (1) можна записати у вигляді:тощо.

Остання формула є найбільш вдалою, тому що, взявши інтервал (9;10) і визначивши матимемо:, тому

. Обчислюємо послідовні наближення з одним запасним знаком за формулами:

Звідси:

Приклад 4. Знайти методом простої ітерації корінь рівняння з точністю 0,01.

Зауваження 2. Виконання умови не гарантує наближеності до точного розв’язку.

Приклад 5. Для розв'язування рівняння х² =а можна прийняти або і, відповідно, записати такі ітераційні процеси:

або .

Перший процес взагалі не збігається, а другий збігається для будь-якого . Другий процес збігається дуже швидко, бо.

Метод простих ітерацій має просту геометричну інтерпретацію. Побудуємо графіки функцій і. Коренем рівняння (8) є абсциса точки перетину графіків. Від початкового наближення х₀ будуємо ламану, абсциси вершин якої є послідов­ними наближеннями кореня. На рис. 5 показано випадок, коли, а на рис. 6 — випадок для

Оцінка похибки методу. Оцінимо похибку n-го наближення:

звідки, звівши подібні члени, отримаємо

Якщо то; тоді оцінка похибки на­ближеннях_п зводиться до оцінки модуля різниці двох послідов­них наближень.

Зауваження 1. Особливість методу простих ітерацій ― ненакопичення похибки обчислень. Похибка обчислень може вплинути на кількість ітерацій, однак не на точність кінцевого результату.

Зауваження 2. Метод простих ітерацій має лінійну швидкість збіжності.