2. Операції над матрицями та їхні властивості

Основними операціями над матрицями є додавання і множення матриць та множення матриць на число.

Нехай А = () і В = () – довільно вибрані () – матриці.

Означення 1.

Сумою матриць А = і В =називають матрицюS = , де= () (;), і записуютьS = А+В.

У розгорнутому вигляді маємо

+ =.

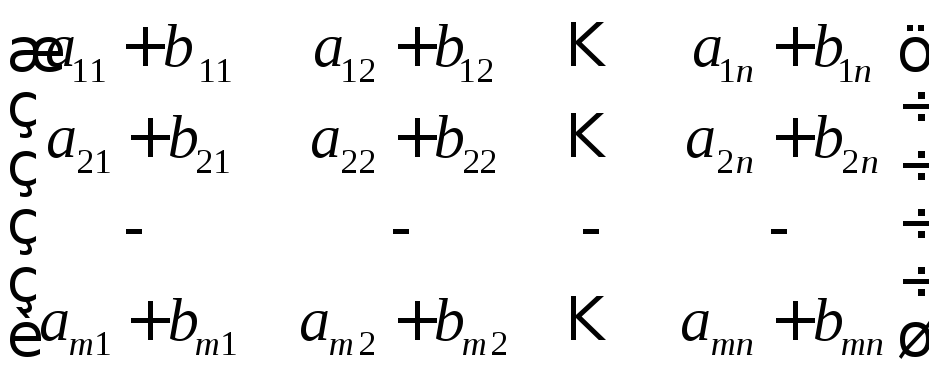Отже, додавання матриць зводиться до додавання всіх пар їхніх відповідних елементів.

Приклад

, ..

З означення суми матриць випливають такі властивості :

1) Операція додавання матриць асоціативне, тобто для будь-яких матриць А,В,С одного й того ж самого розміру (А+В) + С = А + (В+С).

2) Операція додавання матриць комутативне, тобто для будь-яких матриць А і В одного й того ж розміру А+В = В+А.

Матриця, всі елементи якої дорівнюють нулю, називається нульовою матрицею і позначається символом О.

Для будь-якої матриці справджуються рівності

.

Нехай А = () – довільно вибрана (m,n) – матриця і λ – деяке дійсне число.

Означення 2.

Добутком матриці А =на число λ називають матрицею В =, де= λ(;), і записується В=λА.

У розгорнутому вигляді маємо

Таким чином, множення матриці на число зводиться до множення всіх її елементів на це число.

Приклад

З означення добутку матриці на число випливають такі властивості:

1) Операція множення матриці на число асоціативне:

.

2) Операція множення матриці на число дистрибутивна відносно додавання матриць:

.

3) Операція множення матриці на число дистрибутивна відносно додавання чисел:

4) Операція множення матриці на число комутативне:

Означення 3.

Добутком матриці А = на матрицю В =називають матрицю С =, елементи якої визначаються за формулами

; ), (3)

і записують С = АВ.

Формула (3) є правилом множення матриці А на матрицю В. Це правило формулюють так : щоб дістати елемент матриці С , слід елементи і-го рядка матриці А помножити на відповідні елементи к-го стовпця матриці В і добутки додати.

Зауважимо, що формулу (3) можна застосовувати тільки тоді, коли кожен рядок матриці А містить стільки елементів, скільки їх у кожному стовпці матриці В.

Добуток АВ визначений тільки тоді, коли число стовпців матриці А дорівнює числу рядків матриці В, причому число рядків матриці АВ дорівнює числу рядків матриці А, а число стовпців – числу стовпців матриці В.

Приклади

1.

2.

Властивості множення матриць.

1. Операція множення матриць не комутативна.

Проте для деяких пар квадратних матриць А, В може трапитись, що АВ=ВА. Такі матриці називають переставними. Переставними, наприклад, є матриці:

і ,

оскільки

і .

2. Операція множення матриць асоціативна, тобто якщо добутки АВ і ВС визначені,то (АВ)С = А(ВС).

3) Операція множення матриць дистрибутивна відносно операції додавання :

а) якщо добутки АС і ВС визначені, то (А+В)С = АС+ВС;

б) якщо добутки СА і СВ визначені, то С(А+В) = СА+СВ;

4) Якщо добуток АВ матриць А і В визначений, то для будь-якого числа λ

.

Крім розглянутих основних операцій над матрицями застосовується ще одна операція – транспонування матриць.

Транспонуванням матриці А називається таке її перетворення, при якому рядки цієї матриці стають стовпцями з тими самими номерами.

Сума і добуток матриць та добуток матриці на число транспонують за такими правилами :

1. Для будь-яких матриць А і В того самого розміру

.

2. Якщо добуток АВ матриць А і В визначений, то

.

3. Для кожної матриці А і будь-якого числа λ

.

► Доведемо справедливість другого правила. Нехай А = , В =. Елемент, що стоїть в і-му рядку й к-му стовпці матриці, дорівнює елементу, який стоїть у

к-му рядку й і-му стовпці матриці АВ, тобто дорівнює :

.

Проте цей вираз є сумою добутків елементів і-го рядка матриці на відповідні елементик-го стовпця матриці . Отже. ◄

Справедливість правил 1) і 3) пропонуємо довести самостійно.

Нехай А = () і В = () – квадратні матриці порядкуn, тоді добуток АВ визначений і є квадратною матрицею порядку n. Серед квадратних матриць n-го порядку особливу роль відіграє матриця

,

всі елементи головної діагоналі якої дорівнюють одиниці, а інші – нулю. Ця матриця називається одиничною матрицею n-го порядку й позначається символом Е. Для будь-якої матриці А порядку n справджуються нерівності

АЕ = ЕА = А, А0 = 0А = 0.

Квадратна матриця вигляду

називається діагональною матрицею, а матриця вигляду

- скалярною матрицею.

Діагональну матрицю позначають символом (), а скалярну – символом.

Кожна скалярна матриця, очевидно, є діагональною матрицею. Одинична матриця і квадратна нульова матрицяє скалярні, а отже, і діагональні матриці.

Кожна скалярна матриця . переставна з будь-якою матрицею n-го порядку:

А=А