за допомогою двох перестановок з чисел 1, 2, 3,…, n, тобто

,

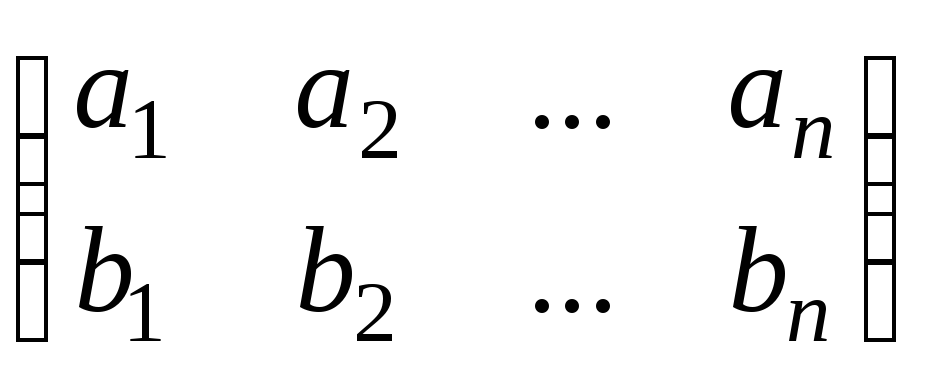причому перестановку а₁, а₂,…, а_n завжди можна вибрати довільно.

Означення 7. Підстановка φ називається парною, якщо сумарне число інверсій у верхній і нижній перестановках парне, в противному разі вона називається непарною.

Приклад. Визначити парність підстановки 6-го степеня

φ =.

У верхній перестановці цього запису 5 інверсій, а в нижній їх 11. Загальне число інверсій в обох перестановках – 16. Отже, підстановка φ парна.

Запишемо підстановку, що розглядається так:

φ =.

У верхній перестановці цього запису 0 інверсій, а в нижній – їх 8. Загальне число інверсій – 8.

Цей приклад показує, що при різних записах даної підстановки парність загального числа інверсій зберігається, а саме число інверсій змінюється.

3. Визначники n-го порядку та їхні властивості

Нехай дано квадратну матрицю n-го порядку

А=.

Означення 8. Визначником (детермінантом) n-го порядку матриці А називається число, яке дорівнює сумі n! доданків, кожний з яких є добутком n елементів, взятих по одному з кожного рядка і кожного стовпця матриці із знаком (-1)^t, де t – число інверсій у підстановці із індексів елементів добутку.

Детермінант матриці А позначають символами

Δ=detA==.

За означенням 8

Δ=.

У цьому записі перші індекси – номери рядків. Другі індекси - номери стовпців визначника матриці А, t – число інверсій у підстановці

.

Знак, з яким член входить до визначника, визначається числом інверсій у перестановці (). Власне він визначається парністю перестановки (): якщо перестановка парна, то член входить до визначника із знаком плюс, в протилежному разі – із знаком мінус.

Зауважимо, що при визначенні знака даного члена визначника за допомогою підстановки, утвореної індексами його елементів, не обов’язково розташовувати множники члена в порядку зростання їхніх перших індексів. Якщо і є один і той самий член, то підстановки

і ,

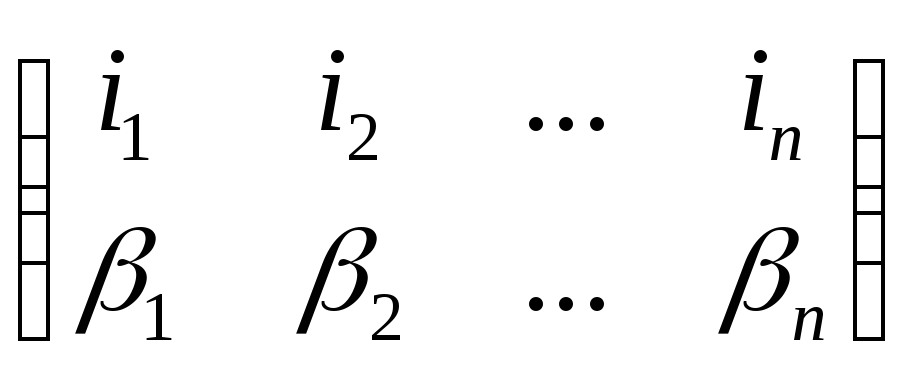як відомо, будуть однієї і тієї самої парності.

Приклад. Обчислити визначник, користуючись лише означенням

Δ=.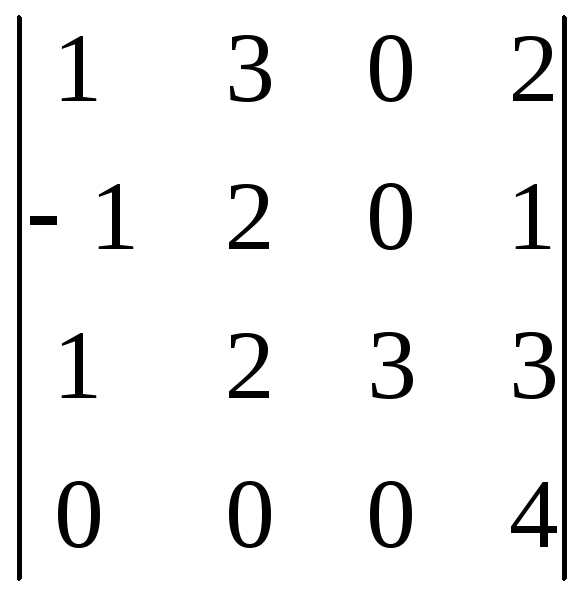

Даний визначник має 4!=24 члени. Відмінним від нуля елементом четвертого рядка є тільки 4. Не дорівнюють нулю два добутки, в які входить 4, а саме: 1∙2∙3∙4 і 3∙(-1)∙3∙4. Перший з них входить у визначник із знаком плюс. Знак другого добутку збігається із знаком числа (-1)^t, де t – число інверсій у підстановці

,

t =1, тому (-1)¹=-1. Отже, Δ=1∙2∙3∙4+3∙1∙3∙4=60.

Розглянемо деякі елементарні властивості визначників n-го порядку, які стосуватимуться умов, за яких визначник дорівнює нулю, і перетворень матриці, які не змінюють її визначника або ж викликають зміни, що легко враховуються.

Властивість 1. Визначник матриці не змінюється при її транспонуванні.

detA=detA^t.

Дана властивість стверджує рівноправність рядків і стовпців визначника: будь-яке твердження про рядки визначника справедливе й для його стовпців і навпаки.

Властивість 2. Якщо який-небудь з рядків (стовпців) визначника складається з нулів, то визначник дорівнює нулю.

► Це твердження безпосередньо випливає з означення 8. Справді, нехай всі елементи i-го рядка визначника є нулі. Оскільки до кожного члена визначника входить як співмножник один елемент i-го рядка, то всі члени визначника дорівнюють нулю, а отже, і визначник дорівнює нулю. ◄

Властивість 3. Якщо у визначнику поміняти місцями будь-які два рядки (стовпці), то визначник змінить знак на протилежний.

(Довести самостійно).

Властивість 4. Визначник, в якому є два однакові рядки (стовпці), дорівнює нулю.

► Нехай у визначнику однакові s-й і k-й рядки. Поміняємо їх місцями, дістанемо визначник detÃ. За властивістю 3, detÃ=–detA. Оскільки переставлено однакові рядки, то визначник detA від цього не зміниться, і тому detÃ=detA. Звідси випливає, що detA=– detA. Отже, detA=0. ◄

Властивість 5. Якщо всі елементи одного з рядків (стовпців) визначника помножити на деяке число λ, то визначник помножиться на λ.

► Припустимо, що всі елементи i-го рядка визначника помножено на число λ. Оскільки до кожного члена визначника входить співмножником один елемент з i-го рядка, то в кожному члені з’явиться множник λ. Тому і визначник помножиться на λ. ◄

Наслідок. Спільний множник всіх елементів будь-якого рядка (стовпця) визначника можна винести за знак визначника.

Властивість 6. Визначник, в якого є два пропорційні рядки (стовпці) дорівнює нулю.

► Нехай k-й рядок визначника detA дістаємо з s-го рядка (k≠s) множенням s-го рядка на деяке число λ, тобто (j=). Винісши спільний множник λ елементівk-го рядка за знак визначника, дістанемо визначник, в якого k-й і s-й рядки будуть однакові. Цей визначник, за властивістю 4, дорівнює нулю. Отже, й визначник detA дорівнює нулю. ◄

Властивість 7. Якщо всі елементи деякого рядка (стовпця) визначника є сумою двох доданків, то такий визначник дорівнює сумі двох визначників:

=+.

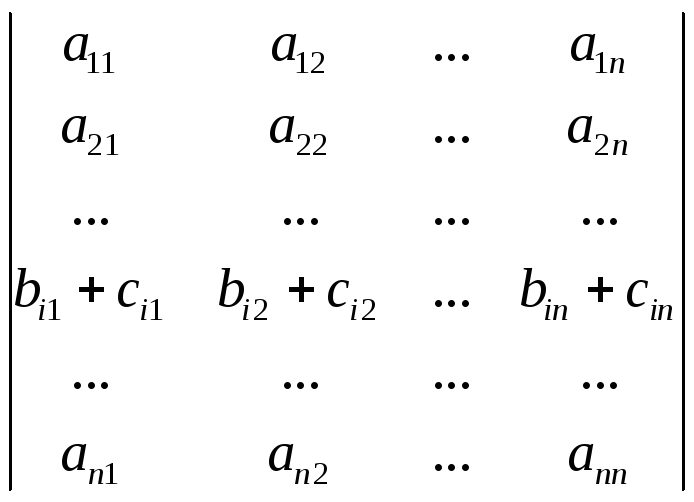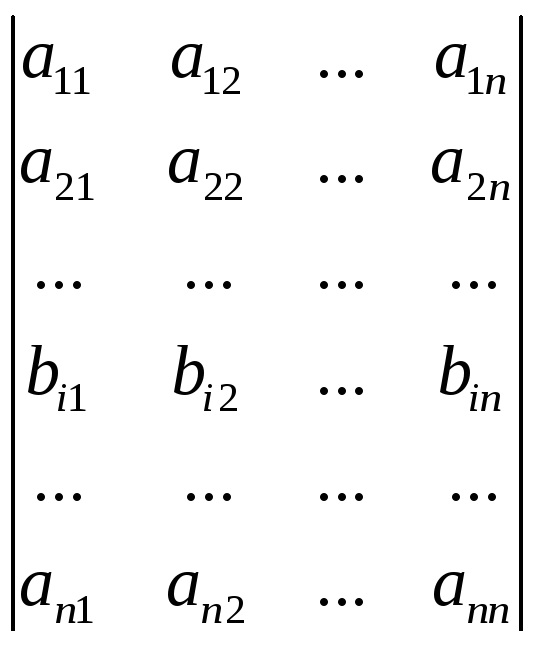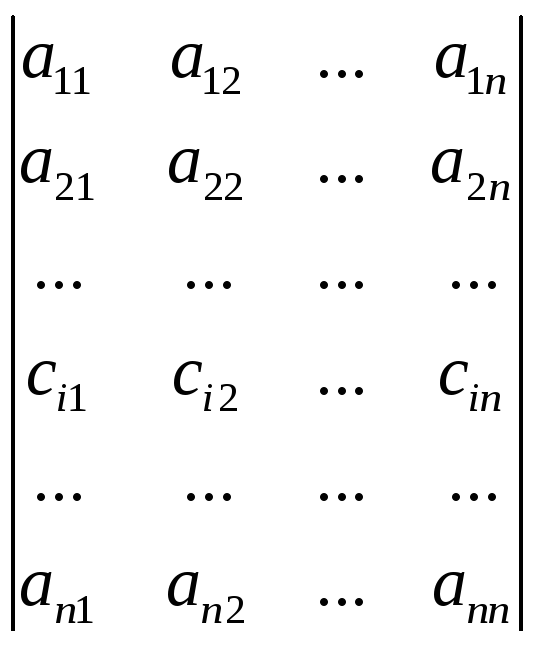Властивість 8. Якщо один з рядків (стовпців) визначника є лінійною комбінацією інших його рядків (стовпців), то визначник дорівнює нулю.

► Справді, нехай i-й рядок визначника detA є лінійною комбінацією m інших його рядків,2≤ m ≤n–1. Тоді кожен елемент i-го рядка є сумою m доданків. За властивістю 7, detA дорівнює сумі m визначників, в кожного з яких i-й рядок буде пропорційний одному з інших його рядків. Всі ці визначники, за властивістю 6, дорівнюють нулю, а тому дорівнює нулю й визначник detA. ◄

Властивість 9. Якщо до одного з рядків (стовпців) визначника додамо інший його рядок (стовпець), помножений на деяке число λ, то визначник не зміниться.

► Справді, припустимо, що до i-го рядка визначника detA додано s-й рядок, помножений на число λ. В новому визначнику detà кожен елемент i-го рядка має такий вигляд: (j=). За властивістю 7, визначникdetà дорівнює сумі двох визначників, перший з яких є detA, а другий дорівнює нулю, оскільки в нього i-й і s-й рядки пропорційні. Отже, detà = detA. ◄