Комбинаторика

Вспомним «дерево вариантов». Обозначим животных цифрами.

Пусть 1 – козёл, 2 – осёл, 3 – мартышка,

4 – мишка.

Получим, что возможных вариантов их расстановки 4∙ 3 ∙ 2 ∙ 1 = 24

В задаче были подсчитаны всевозможные комбинации из четырёх элементов, отличающиеся друг от друга только порядком расположение в них элементов. Такие комбинации называются перестановками из нескольких элементов.

ОПРЕДЕЛЕНИЕ: Комбинации из n элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются перестановками

из n элементов.

Лейбницем в 1666 г. в работе «Рассуждение о комбинаторном искусстве» впервые дано научное обоснование теории сочетаний и перестановок.

Число всевозможных перестановок из n элементов обозначают Рn (Р- первая буква французского слова permutation – перестановка).

С помощью правила произведения можно обосновать, что Рn= n∙(n-1) ∙… ∙3∙2∙1.

После применение переместительного закона умножения перепишем формулу в виде:

Pn=1∙2∙3∙…∙ (n-1) ∙n.

Для сокращённой записи произведения первых n натуральных чисел используется факториал n!

Рn= n!

21

Упражнения

1)5 друзей решили сфотографироваться. Сколькими способами они могут сесть? (120)

2)Сколько фигурок можно составить из Танграма? (5040)

3)Свидетель ДТП заметил номер машины, совершившей наезд. Он запомнил, что в номере буквы АВ и цифры 2, 3, 4, но не помнит их порядок. Сколько вариантов номеров нужно проверить милиции, чтобы найти нарушителя? (6)

4)Сколько различных пятизначных чисел, все цифры которых различны,

5)Турист решил объехать 10 городов Золотого кольца. Сколько у него существует вариантов выбора маршрута?

6)На балу собрались 10 дам и 10 кавалеров. Сколькими способами они могут разбиться на пары ?

7)Имеется множество чисел N = {1,2,3,4,5}.

Сколько существует трёхзначных чисел, все цифры которых различны? Сколько существует четырёхзначных чисел, все цифры которых различны? Сколько существует пятизначных чисел, все цифры которых различны?

Размещения

Задача. Имеется множество чисел N = {1,2,3,4,5}.

а) Сколько существует пятизначных чисел, все цифры которых различны? Решение: Данные комбинации чисел будут перестановками, Р5 = 5! = 120 б) Сколько существует трёхзначных чисел, все цифры которых различны?

Решение: Это уже не перестановки. Первую цифру можно выбрать 5 способами, вторую – четырьмя, третью цифру – тремя способами, т.е. число трёхзначных чисел будет 5× 4 × 3 = 60

22

в) Сколько существует четырёхзначных чисел, все цифры которых различны?

Решение: Это также не перестановки. Первую цифру можно выбрать 5 способами, вторую – четырьмя, третью цифру – тремя способами, четвёртую

– двумя способами, т.е. число четырёхзначных чисел будет 5× 4 × 3 × 2 = 120

Имеется n различных предметов. Сколько из них можно составить k- расстановок?

При этом две расстановки считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.

Такие комбинации, отличающиеся друг от друга порядком элементов и составом, называются размещениями.

ОПРЕДЕЛЕНИЕ: Размещением из n элементов по k (k £ n) называется любое подмножество данного множества, состоящее из любых k элементов, взятых в определённым порядке из данных n элементов.

Число размещений из n элементов по k обозначают Аnk (читают А из n по

k).

Размещения – это упорядоченные подмножества данного множества.

По правилу произведения число упорядоченных k-элементных подмножеств множества N, состоящего из n элементов, находится как произведение чисел: n (n – 1) (n – 2) (n – 3)….( n – k + 1). Или число размещений из n элементов по k вычисляется по формуле:

Можно сказать что размещения из п элементов по п – это перестановки из п-элементов. Сравним число таких комбинаций, вычисленное по формуле размещений и по формуле перестановок:

23

Изучением «размещений» впервые занимался Якоб Бернулли во второй части своей знаменитой книги «Искусство предугадывания», опубликованной в 1713 г. Он же ввел соответствующий термин.

Яков (Якоб) Бернулли

Математик, физик, астроном и механик Яков Бернулли (1654 — 1705) родился в Базеле (Швейцария). Отец хотел, чтобы сын был священником, и поэтому Я. Бернулли, поступив в Базельский университет, в основном изучал теологию и языки. Он владел немецким, французским, английским, итальянским, латинским и греческим языками.

Но больше всего его привлекала математика, которую он изучал тайком от отца. Наиболее значительные достижения Якова I в развитии анализа бесконечно малых, теории рядов, вариационного исчисления и теории вероятностей. В 1687г., ознакомившись с первыми работами Г.Лейбница по дифференциальному исчислению (1684г.), Бернулли применил новые идеи к изучению свойств ряда кривых: логарифмические спирали, открытой им лемнискаты, цепной линии и др. Определил площадь сферического треугольника, вычислил площади конусоидальных и сфероидальных поверхностей, произвел многочисленные квадратуры и спрямления. Книга Бернулли "Арифметические приложения о бесконечных рядах и их конечных суммах" (1689-1704гг.) явилась первым руководством по теории рядов. Бернулли – это целая семья математиков. Совместно с братом Иоганном I, Яков положил начало вариационному исчислению. Выдвинул и частично решил изопериметрическую задачу и задачу о брахистохроне, или кривой быстрейшего спуска, поставленную братом

24

Иоганном. В труде "Искусство предложения" Яков I в 1713г. решил некоторые задачи комбинаторики; открыл числа, позднее названные числа Бернулли; доказал так называемую теорему Бернулли - частный случай закона больших чисел, имеющего большое значение в теории вероятностей и ее приложениях к статистике; построил математическую модель для описания серии независимых испытаний (схема Бернулли). Благодаря его работам теория вероятностей приобрела важнейшее значение в практической деятельности.

Решение задач

Задача № 1. Сколько двузначных чисел можно составить из чисел 1,2,3,4?

Задача № 2. Сколько всего 7-значных телефонных номеров, в каждом из которых цифры не повторяются?

Это размещения из 10 элементов по 7.

Задача № 3. Сколькими способами могут занять 1, 2, 3 места 8 команд - участниц городского турнира по волейболу?

0,1,2,3,4,5,6,7,8,9?

Это размещения из 10 по 2, но нужно исключить те числа, первая цифра которых 0, таких чисел 9.

25

Сочетания

Задача: Имеются 5 различных соков. Сколько различных коктейлей можно получить из этих соков, если смешивать в каждом по три вида соков?

Зависит ли вкус коктейля от того, в каком порядке находятся в нём соки? Конечно, нет. Т.е. это не размещения.

Подсчитаем вначале, сколько будет размещений из 5 по 3:

Но размещения АБВ и БВА в коктейле дают один и тот же результат, всего таких перестановок Р3 = 3! = 6.

Значит, число коктейлей в 6 раз меньше возможного числа размещений,

5!

60: 6 = 10, или (5 - 3)!×3!

ОПРЕДЕЛЕНИЕ: Число всех комбинаций из n элементов по k, отличающиеся друг от друга только составом элементов, называются

сочетаниями из n элементом по k.

размещений. В самом деле, составим сначала все k-сочетания из n элементов, а потом переставим входящие в каждое сочетание элементы всеми возможными

26

Число сочетаний из n элементов по k вычисляется по формуле:

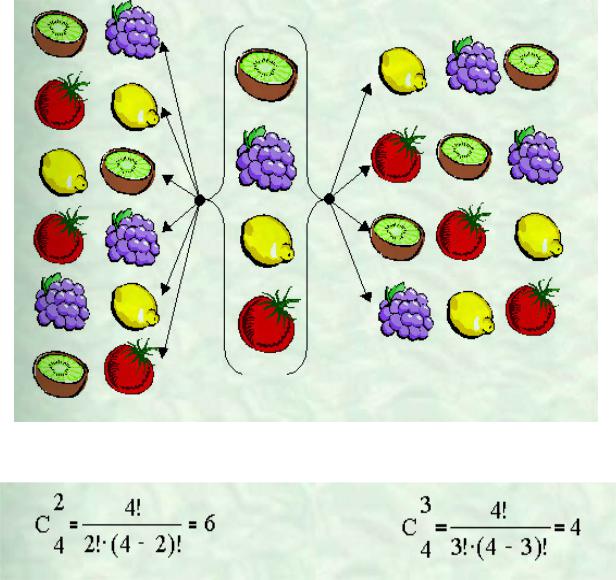
Задача . Имеются киви, лимон, помидор, виноград. Вычислим, сколькими способами можно их взять, если можно брать по 2 штуки. А если брать по 3 штуки?

Проверим наше решение по формуле числа сочетаний

Число сочетаний имеет некоторые свойства

27

Задача 1. Из 15 членов туристической группы надо выбрать 3 дежурных. Сколькими способами можно сделать этот выбор?

Решение: Речь идёт о сочетаниях из 15 элементов по 3.

Задача № 2. В группе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в олимпиаде?

Задача 3. В классе 30 учеников. Нужно разделить их на «миги» по 5 человек. Сколькими способами это можно сделать? (142506)

Упражнения

1)В магазине продается белая, черная и синяя ткань. Нужно купить ткань двух различных цветов. Из какого числа вариантов приходится выбирать?

2)Иван-царевич едет в гости в соседнее королевство и везет в подарок трем дочерям короля перстень, браслет и ожерелье. Что кому дарить, он пока не решил. Сколько у него вариантов распределить подарки?

3)Поэт-модернист написал стихотворение, в котором первая строка «Хочу пойти гулять куда-нибудь», а все остальные строки разные и получены из

28

первой перестановкой слов. Какое наибольшее количество строк может быть в этом стихотворении?

4) В некотором государстве кабинет министров состоит из 10 человек. Сколькими способами они могут выбрать из состава кабинета премьерминистра, первого и второго вице-премьеров?

Дополнительные задачи:

1.Сколько экзаменационных комиссий, состоящих из 7 человек, можно создать из 14 преподавателей? (ответ: 3432)

2.При встрече 12 человек обменялись рукопожатиями. Сколько сделано рукопожатий? (ответ: 66)

3.На плоскости даны 5 точек, никакие три из них не лежат на одной прямой. Сколько прямых можно провести через эти точки? (ответ: 10)

4.Сколько диагоналей в выпуклом десятиугольнике? (ответ: 35)

5.В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем? (5×3=15)

6.У Димы есть пять шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами он сможет украсить ими пять елок, если на каждую требуется надеть ровно один шарик? Р5 = 5! = 120

7.Вите хочется купить пять разных книг. Книги стоят одинаково, а денег хватает только на три книги. Сколькими способами Витя может выбрать три

29

помощника. Сколькими способами это можно сделать?

11.Сколькими способами можно купить две порции мороженого, если в продаже есть вафельные стаканчики, конусы, шоколадные брикеты и эскимо?

12.Сколькими способами можно выложить на полке в ряд 5 книг? 13.«Проказница Мартышка, Осёл, Козёл и косолапый Мишка затеяли

сыграть квартет». Мишке поручили принести со склада 8 какихнибудь музыкальных инструментов из имеющихся там 13. Сколько способов выбора есть у Мишки?

14.В гимназии в 9 классе в понедельник 6 уроков: математика, русский, литература, история, английский и физкультура. Сколько вариантов расписания в этом классе можно составить на понедельник?

15.Ваня, Петя, Саша и Коля носят фамилии Ваньков, Петров, Санеев и Колов. Известно, что: Ваня и Санеев – отличники; Петя и Ваньков – троечники; Ваньков ростом выше Петрова; Коля ростом ниже

Петрова; Саша и Петя одинакового роста; Определите фамилию каждого мальчика.

16.На заводе работали три друга: слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семёнов. Известно, что: у слесаря нет ни братьев, ни сестёр и он самый младший из друзей; Семёнов, женатый на сестре Борисова, старше токаря. Определите фамилии друзей.

30