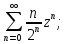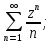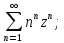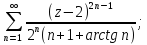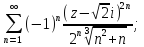- •Программа курса по тфкп
- •Вопросы Для экзамена по математическому анализу
- •Тематика практических занятий.
- •Комплексные числа. Линии и области в с.
- •Функции комплексного переменного. Рельеф функции. Дифференцируемость функций.
- •Линейные и дробно-линейные функции.
- •Вопросы и упражнения для самопроверки к занятиям 1-3.
- •Элементарные функции.
- •Решение уравнений с.
- •Степенные ряды.
- •Контрольная работа.
- •Интеграл в с.
- •Интегрирование голоморфных функций.
- •Ряды Тейлора.
- •Ряды Лорана. Изолированные особые точки голоморфной функции.
- •Приложение №1. Контрольные задания по курсу тфкп.
- •Список рекомендуемой литературы.
Степенные ряды.
Основные вопросы теории:
Определение степенного ряда. Область сходимости степенного ряда.
Теорема Коши-Адамара. Радиус и круг сходимости степенного ряда.
Почленное дифференцирование рядов.
Геометрический ряд.
На занятии рекомендуется решить задачи:
Найти область сходимости рядов:
Используя геометрический ряд, разложить в степенной ряд в окрестности
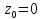 функции
функции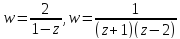 . Найти радиус сходимости полученных
рядов.
. Найти радиус сходимости полученных
рядов.Разложить в степенной ряд в окрестности
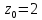 функции
функции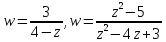 .
.Используя возможность почленного дифференцирования степенного ряда, вычислить сумму ряда
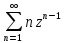 .
.
По теме занятия рекомендуется самостоятельно решить задачи:
№ 334, 336, 338, 340, 341, 346, 347, 348, 381, 393.
Занятие № 7.
Контрольная работа.
Примерные варианты контрольной работы по темам занятий №№ 1-6 содержится в Приложении 1 (с. 28, задачи 1-6).
Занятие № 8.
Интеграл в с.
Основные вопросы теории:
Гладкие и кусочно-гладкие кривые, односвязные и многосвязные области в С.
Определение криволинейного интеграла и его свойства.
Применение криволинейного интеграла к вычислению площадей. Формула Грина.
На занятии рекомендуется решить задачи:
Вычислить интегралы по определению: а)
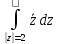 ;
б)
;
б)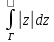 ,
Г – радиус-вектор точки2-i;
в)
,
Г – радиус-вектор точки2-i;
в)
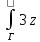 4dz,
Г={z ∈
С| |z|=1, 0 ≤ arg z ≤ π};
4dz,
Г={z ∈
С| |z|=1, 0 ≤ arg z ≤ π};Пусть Г – замкнутая кривая, ограничивающая фигуру площади S (гладкая). Используя формулу S=
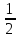
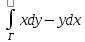 ,
доказать равенства:
а)
,
доказать равенства:
а)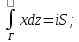 б)
б)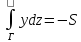 ;
в)
;
в)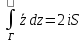 ;
;
По теме занятия рекомендуется самостоятельно решить задачи:
№№ 352, 353, 358.
Занятие № 9.
Интегрирование голоморфных функций.
Основные вопросы теории:
Интегральная теорема Коши для односвязных областей.
Обобщение интегральной теоремы Коши на случай многосвязных областей.
Интегральная формула Коши.
На занятии рекомендуется решить задачи:
Вычислить интегралы:
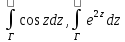 Г
– радиус-вектор точки 2. Зависит ли
величина интегралов от формы пути
интегрирования: А от направления?
Г
– радиус-вектор точки 2. Зависит ли
величина интегралов от формы пути
интегрирования: А от направления?
Вычислить интегралы: а)
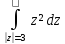 ;
б)
;
б)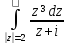 ;
в)
;
в)
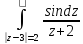 ;
г)
;
г)
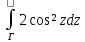 ,
Г={z∈
С| |z|=2, Im
z≥0}
,
Г={z∈
С| |z|=2, Im
z≥0}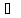 {z∈
С| |Re z|≤2,
Im
z=0,
|Re z|≤2}
;
д)
{z∈
С| |Re z|≤2,
Im
z=0,
|Re z|≤2}
;
д)
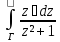 ;
;
е)
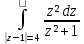 ;
ж)
;
ж)
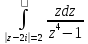 ;
з)
;
з)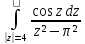 ;
и)
;
и)
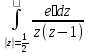 ;
к)
;
к)
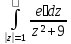 ;
;
По теме занятия рекомендуется самостоятельно решить задачи:
№№ 365, 366, 368, 371, 376.
Занятие № 10.
Ряды Тейлора.
Основные вопросы теории:
Теорема о разложении голоморфной функции в степенной ряд. Ряды Тейлора. Интегральные и дифференциальные формулы для коэффициентов ряда Тейлора.
Неравенства Коши. Теорема Леувилля.
Ряды Тейлора для основных элементарных функций (показательной, тригонометрических, логарифмических).
На занятии рекомендуется решить задачи:
Непосредственным вычислением коэффициентов найти разложение в ряд Маклорена функции w=cos t.
Разложить в ряд Маклорена в окрестности z0 =
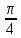 функцию w
= sin
t.
функцию w
= sin
t.Найти первые 4 члена разложения в ряд Маклорена функций: а) w=
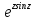 ;
б)
w=
;
б)
w=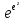 ;
в)
w=ln(1+
;
в)
w=ln(1+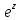 );
);Разложить в ряд Маклорена функции: а) w=
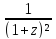 ;
б)
w=sin²z;
;
б)
w=sin²z;Вычислить интегралы: а)
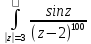 dz;
б)
dz;
б)
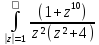 ;
;Разложить в ряд Маклорена функцию w=
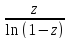 , доопределив
ее в точке z=0.
, доопределив
ее в точке z=0.
По теме занятия рекомендуется решить задачи:
№№ 385, 386, 390, 395, 399.
Занятие № 11.