- •Метод гаусса решения систем линейных уравнений и его модификации
- •Кафедра: «Математического анализа»
- •Введение
- •Компактная схема Гаусса
- •Компактная схема Гаусса
- •Порядок заполнения таблицы (прямой ход):
- •Обратный ход:
- •Модификация Краута – Дулитла
- •Порядок заполнения таблицы, прямой ход:
- •3. Схема Гаусса с выбором главного элемента
- •Задания к лабораторной работе по теме «Решение систем линейных уравнений»
- •Тесты для защиты лабораторной работы Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •1. Последние строки разделов и всех столбцов, кромеи, это результат:
- •Список литературы
- •Михащенко Татьяна Николаевна Метод гаусса и его модификации
- •640669, Г. Курган, ул. Гоголя, 25
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Курганский государственный университет
Кафедра математического анализа
Метод гаусса решения систем линейных уравнений и его модификации
Методические указания к выполнению лабораторных работ по дисциплине Численные методы для студентов направлений (специальностей) 010100 Математика, 050100 Педагогическое образование (050101, 050202)
Курган 2014
Кафедра: «Математического анализа»
Дисциплина: «Численные методы»
010100 Математика,
050100 Педагогическое образование (050101, 050202)
Составили: канд. пед. наук, доц. Т.Н. Михащенко (теоретическая часть,
варианты заданий, общая редакция);
студент Лобков В.Ю. (примеры расчета, набор текста).
Введение
Известно, что почти 75% всех расчётных математических задач приходится на решение систем линейных алгебраических уравнений, так как математические модели тех или иных явлений или процессов или сразу строятся как линейные, или сводятся к ним. Поэтому не трудно переоценить роль, которую играет выбор эффективного способа решения системы линейных уравнений. Современная вычислительная математика располагает большим арсеналом методов, а математическое обеспечение ЭВМ – многими пакетами прикладных программ, позволяющих решать различные линейные системы.
Целью данного методического пособия является ознакомление студентов с различными модификациями самого распространенного метода решения систем линейных уравнений – метода Гаусса.
В пособии содержатся методические рекомендации по организации вычислений, задание для лабораторной работы по теме «Методы решения систем линейных уравнений», все схемы снабжены подробными инструкциями по их применению и алгоритмизированы для программирования на ЭВМ.
На выбор студенту предлагается несколько модификаций проведения и оформления вычислений: полная и компактная схемы Гаусса, модификация Краута-Дулитла, схема Гаусса с выбором главного элемента.
Компактная схема Гаусса
Компактная схема Гаусса дает экономный способ записи вычислений и полностью соответствует традиционному методу Гаусса, изучаемому в курсе алгебры.
Суть метода Гаусса….
Рассмотрим порядок составления схемы для системы четырёх уравнений с четырьмя неизвестными. Все результаты вычислений будем записывать в одну таблицу (таблица 1).
Таблица 1
Компактная схема Гаусса
|
|
i |
ai1 |
ai2 |
ai3 |
ai4 |
ai5 |
ai6 |
|
|
|
I |
1 |
a11 |
a12 |
a13 |
a14 |
a15 |
a1j = a16 |
| |
|
2 |
a21 |
a22 |
a23 |
a24 |
a25 |
a2j = a26 |
| ||
|
3 |
a31 |
a32 |
a33 |
a34 |
a35 |
a3j = a36 |
| ||
|
4 |
a41 |
a42 |
a43 |
a44 |
a45 |
a4j = a46 |
| ||
|
|
1 |
b12 |
b13 |
b14 |
b15 |
a16 / a11= b16 |
| ||
|
II |
2 |
|
a |
a |
a |
a |
a |
| |
|
3 |
|
a |
a |
a |
a |
a |
| ||
|
4 |
|
a |
a |
a |
a |
a |
| ||
|
|
|
1 |
b |
b |
b |
a |
| ||
|
III |
3 |
|
|
a |
a |
a |
a |
| |
|
4 |
|
|
a |
a |
a |
a |
| ||
|
|
|
|
1 |
b |
b |
a |
| ||
|
IV |
4 |
|
|
|
a |
a |
a |
| |
|
V |
|
|
|
|
1 |
x4 |
|
| |
|
|
|
|
1 |
|
x3 |
|
| ||
|
|
|
1 |
|
|
x2 |
|
| ||
|
|
1 |
|
|
|
x1 |
|
| ||

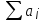

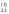
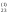


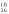
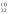
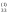
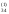
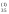
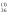

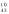
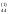
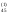
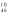

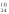

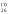 /a
/a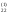 =b
=b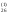
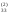

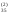
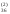
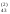
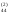
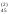
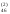
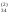
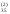
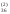 /a
/a =b
=b