8. Графическое представление результатов измерений

Графический способ представления результатов измерений широко используется на практике. Рассмотрим правила, которые применяются при построении графиков.

1) Графики строятся на бумаге, снабженной координатной сеткой (например, миллиметровой).

2) Каждый график подписывается.

3) Наносятся координатные оси графика.

4) На концах осей указываются откладываемые физические величины и их размерности. Обычно порядок масштаба, т.е. также выносится на конец оси. Расшифровка обозначений дается либо в тексте, либо в надписи под графиком.

5) Масштабные деления откладываются через равные промежутки. Расстояние между делениями по оси абсцисс и ординат можно выбирать различными.

6) Масштаб должен быть простым, поэтому на оси наносят масштабные деления так, чтобы расстояние между делениями составляло 1, 2, 5 единиц измеренной величины (или 0.1, 0.2, 0.5, или 10, 20, 50 и т.д.).

7) Нумеруют масштабные деления через равные промежутки, так чтобы числа не сливались.

8) Точка пересечения осей не обязательно должна соответствовать нулю по каждой из осей, кроме тех случаев, когда это необходимо.

9) Начало отсчета по осям и масштабы следует выбирать так, чтобы график занял всю координатную плоскость.

10) После построения осей наносят экспериментальные точки, обозначая их маленькими кружками, квадратиками и т.д.

11) Если на одной координатной плоскости строится несколько графиков, то для точек выбираются разные обозначения. Затем от каждой точки вверх, вниз и вправо, влево откладывают отрезки, соответствующие погрешностям (доверительным интервалам) точек в масштабах осей.

12) Если погрешность по одной из осей (или по обеим осям) оказывается слишком малой, то предполагается, что она отображается на графике размером самой точки.

13) По экспериментальным точкам строится теоретический график той функции (линейной, квадратичной, экспоненциальной, тригонометрической и т.д.), которая отражает физическую закономерность, выраженную в виде соответствующей формулы. Причем, сам график должен лежать в пределах погрешностей каждой из экспериментальных точек. В случае явной нелинейности, точки соединяют «наилучшей» плавной кривой.

В лабораторном практикуме встречаются два случая: проведение теоретического графика для нахождения из эксперимента неизвестных параметров функции (тангенса угла наклона прямой, показателя экспоненты и т.д.) либо делается сравнение предсказаний теории с результатами эксперимента.

В первом случае график соответствующей функции проводится "на глаз" так, чтобы он проходил по всем областям погрешности возможно ближе к экспериментальным точкам. При проведении графика "на глаз" рекомендуется пользоваться зрительным ощущением равенства нулю суммы положительных и отрицательных отклонений точек от проводимой кривой.

Во втором случае график строится по результатам расчетов, причем расчетные значения находятся не только для тех точек, которые были получены в опыте, а с некоторым шагом по всей области измерений для получения плавной кривой. После проведения теоретической кривой расчетные точки с графика убираются.

Если в расчетную формулу входит уже определенный (или заранее известный) экспериментальный параметр, то расчеты проводятся как со средним значением параметра, так и с его максимальным и минимальным (в пределах погрешности) значением. На графике в этом случае изображается кривая, полученная со средним значением параметра, и полоса, ограниченная двумя расчетными кривыми для максимального и минимального значений параметра (рис.2а).

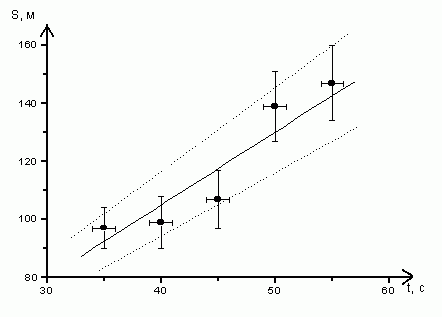
Рис.2 График: а) экспериментальной зависимости;

б) линеаризованной зависимости.

В качестве примера рассмотрим случай, когда необходимо найти угловой коэффициент для линеаризованной зависимости, построенной в осях, со свободным членом(рис.2б).

Графически угловой коэффициент можно найти как тангенс угла наклона прямой, т.е. отношение произвольного приращения вдоль осик соответствующему приращениювдоль осис учетом масштаба из графика:. Необходимо учесть, что угловой коэффициент может иметь различный знак в зависимости от ориентации прямой в выбранной системе отсчета.