Перпендикулярность

Тема: Перпендикулярность прямых и плоскостей в пространстве

План:

1. Общие методические замечания

2. Перпендикулярность двух прямых

3. Перпендикулярность прямой и плоскости

4. Перпендикулярность двух плоскостей

(1) В этой теме рассматривается основной вопрос с взаимного расположения прямых и плоскостей с точки зрения отношения перпендикулярности. Схема изучения состоит из:

1. Перечисляются логические возможности взаимного расположения

   1. перпендикулярность двух прямых

   2. перпендикулярность прямой и плоскости

   3. перпендикулярность двух плоскостей

2. Анализируется вопрос о том, осуществляются ли эти возможности

3. Решается вопрос о единственности

Отметим, что при рассмотрении второго вопроса можно решать конструктивные задачи (на воображаемый чертеж). Например, прямая и плоскость:

1. Даны прямая и точка

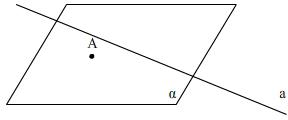
2. Дана плоскость

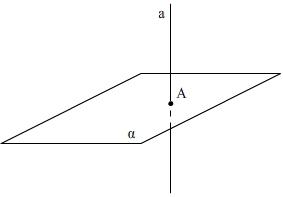
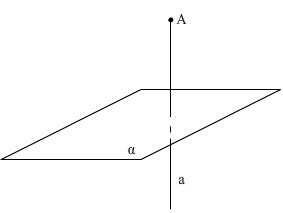
Обратить внимание учащихся на то, что на таких задачах показывается существование. Остановимся на таких особенностях этой темы, как решение стереометрических задач.

Роль задач велика. Так как эти задачи имеют большое практическое значение. Появляется больше задач на вычисление, так как вводится понятие расстояния.

Важную роль играет теорема о трех перпендикулярах.

Можно отметить методическую особенность этой темы: усиление роли задач. То есть, движение не от теории к задачам, а от задач к теории.

(2) Понятие перпендикулярности двух прямых в пространстве рассматривается так же, как на плоскости.

Сначала мы демонстрируем и обсуждаем окружающую нас действительность о взаимном расположении двух перпендикулярных прямых.

Чтобы подвести к определению перпендикулярных прямых, достаточно поставить задачу: дана прямая , построить прямую, перпендикулярную ей на плоскости.

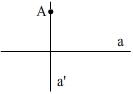
С помощью прямоугольного треугольника мы показываем существование.

Мы решили вопрос о существовании.

Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

Решим вопрос о единственности: доказать, что через любую точку прямой можно провести прямую, перпендикулярную ей в пространстве.

Решение:

Точка принадлежит прямой

1. построить плоскость

2. в этой плоскости можно провести такую прямую по теореме 2.3

3. такая прямая единственна (по этой же теореме)

Теорема. Признак перпендикулярности (перпендикулярность через параллельность).

Пересекающиеся прямые, соответственно параллельные перпендикулярным прямым сами перпендикулярны.

1. две прямые на плоскости (методом от противного)

2. лежат в разных плоскостях

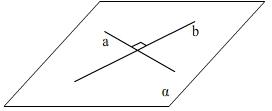
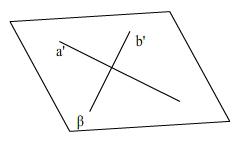
(3) Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой в этой плоскости.

Как проводить перпендикулярность прямой и плоскости?

Берем угольник и двумя измерениями проверяем (2 угольника). Берется нитка с грузиком или прибор-уровень.

Показали существование этого случая и можно перейти к признаку, который гарантирует перпендикулярность прямой и плоскости.

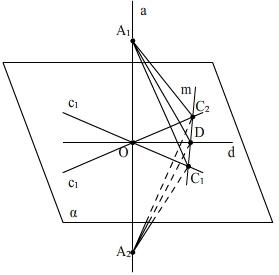
Идея доказательства заключается в том, что выполняется дополнительное построение: проводим . Показать:

Рассматриваем равнобедренные треугольники:

- медиана, а значит и высота в треугольнике

Покажем, что через любую точку данной прямой можно провести перпендикулярную ей плоскость.

По предложенному случаю: провести прямую перпендикулярную прямой через точку .

.

После изучения этих случаев можно провести математический диктант на закрепление определений и признаков типа: запишите символически признак перпендикулярности, постройте…, какие применяются признаки перед определением? И так далее.

Теорема. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

Заметим, что именно здесь рассматривается вопрос о расстоянии между точкой и плоскостью, а именно дается определение перпендикуляра, рассматривается круг задач на вычисление.

Пример. Как найти расстояние от точки до плоскости?

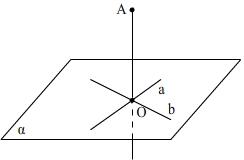
- расстояние.

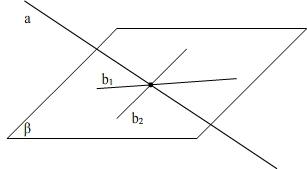
(4) Перпендикулярность двух плоскостей. У Погорелова доказательство проводится через третью плоскость. У Атанасяна через двугранный угол.

Две пересекающиеся плоскости называются перпендикулярными, если какая либо плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Вопросы:

1. Как проверить, что плоскости перпендикулярны?

2. Как построить?

Ответы:

1. На практике проверяют через отвес, уровень.

2. На этот вопрос отвечает признак перпендикулярности

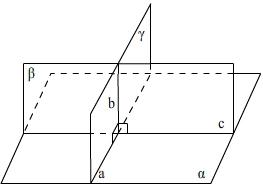
Доказательство:

1. 

2. 

3. 

Задача: даны прямая и плоскость . Провести через прямую плоскость перпендикулярную .

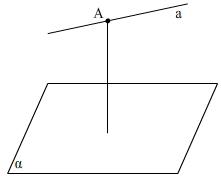
Возьмем точку на прямой . Проведем прямую через точку перпендикулярно .

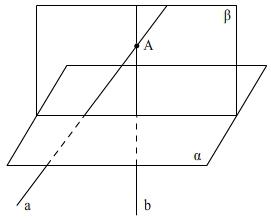
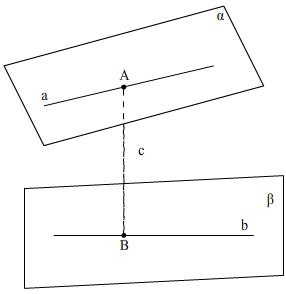
Расстояние между скрещивающимися прямыми.

Общий перпендикуляр:

- перпендикуляр

Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходящими через эти прямые.

Итоговая контрольная должна содержать задания:

1. Отыскать расстояние от точки до плоскости (опустить перпендикуляр).

2. Связь между длинами отрезков и их проекциями.

3. Перпендикуляры и наклонные (теорема о трех перпендикулярах).

По итогам двух тем (параллельность и перпендикулярность) можно провести занятие в виде теста или математического диктанта. На этом занятии можно поставить вопросы типа:

1. Запишите словесно аксиому…(группы С).

2. Изобразите и запишите символически аксиому, позволяющую строить плоскости (на каком основании можно строить плоскости).

3. Сформулируйте определение…

4. Запишите символически и выполните чертеж признака…

5. Какие преимущества имеет признак перед определением?

6. Как провести (построить), например: через заданную точку прямую параллельную плоскости?

7. Как определить расстояние от точки до плоскости; расстояние между двумя плоскостями; расстояние между скрещивающимися прямыми?

Дополнение.

Дано: Доказать:

Дано: Доказать:

При доказательстве первой теоремы через прямую проводят две различные плоскости и , которые пересекают как плоскость , так и плоскость соответственно по прямым и , и , причем и .

Прямая пересекает плоскость в точке пересечения прямых и , а плоскость - в точке пересечения прямых и . Отсюда следует, что .

Другая теорема доказывается от противного.