
МатАн_ЛинАлг_080100 / МА_экз_1курс_экономика_заочн
.doc+: -1
I:
S:
Чему равна вторая производная функции
![]() в
точке
в
точке
![]() ?
?
+: 0
I:
S:
Чему равна вторая производная функции
![]() в
точке
в
точке
![]() ?
?
+: 3
I:
S:
Чему равна вторая производная функции
![]() в
точке
в
точке
![]() ?
?
+: 7
I:
S:
Чему равна вторая производная функции![]() в точке
в точке
![]() ?
?
+: -9
I:
S:
Чему равна вторая производная функции
![]() в
точке
в
точке
![]() ?
?
+: 4
I:
S:
Чему равна вторая производная функции
![]() в
точке
в
точке
![]() ?
?
+: 1
I:
S:
Чему равна вторая производная функции
![]() в
точке
в
точке
![]() ?
?
+: 4
I:
S:
Чему равна вторая производная функции
![]() в
точке
в
точке
![]() ?
?
+: 0
I:
S:
Чему равна вторая производная функции
![]() в
точке
в
точке
![]() ?
?
+: 3
V2: Дифференциал
I:
S:
Значение функции
![]() в
точке
в
точке
![]() можно
вычислить по формуле …
можно
вычислить по формуле …
-:
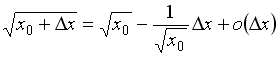
-:

-:
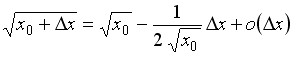
+:
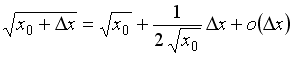
I:
S:
Значение функции
![]() в
точке
в
точке
![]() можно
вычислить по формуле …
можно
вычислить по формуле …
-:

-:
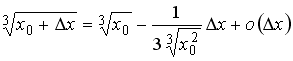
-:
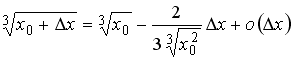
+:

I:
S:
Значение функции
![]() в
точке
в
точке
![]() можно
вычислить по формуле …
можно
вычислить по формуле …
-:

-:
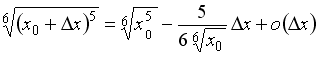
+:
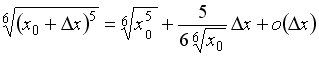
-:

I:
S:
Значение функции
![]() в
точке
в
точке
![]() можно
вычислить по формуле …
можно
вычислить по формуле …
-:
![]()
-:
![]()
-:
![]()
+:
![]()
V1: Исследование функции и построение графика
V2: Точки экстремума
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
+: 0
-: Функция не имеет экстремума
-: 3
-:
![]()
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
-: Функция не имеет экстремума
+: 0
-: -3
-: 3
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
-: -6
+: 6
-: 1
-: 5
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
+: 0
-: 8
-: Функция не имеет экстремума
-: 9
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
-: 2
+: Функция не имеет экстремума
-: 1
-: 8
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
-: 0
+: 6
-: -6
-: 5
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
-: 0
-: 2
+: -2
-: Функция не имеет экстремума
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
-: 4
+: Функция не имеет экстремума
-: 0
-: 2
I:
S:
Сумма координат точек, в которых функция
![]() достигает экстремума, равна
достигает экстремума, равна
-: 0
+: -2
-: 2
-: 1
I:
S:
Сумма координат точек, в которых функция
![]() достигает
экстремума, равна
достигает
экстремума, равна
-: 0
-: 3
+: 1
-: Функция не имеет экстремума
I:
S:
При каком значении х функция
![]() имеет минимум?
имеет минимум?
-: 0
+: 4
-: Ни при каком х
-: 2
I:
S:
При каком значении х функция
![]() имеет минимум?
имеет минимум?
-: 0
-: 4
-: 2
+: Ни при каком х
I:
S:
При каком значении х функция
![]() имеет максимум?
имеет максимум?
+: 1
-: 5
-: Ни при каком х
-: 3
I:
S:
При каком значении х функция
![]() имеет максимум?
имеет максимум?
-: Ни при каком
-: -4
+: 0
-: 4
I:
S:
При каком значении х функция
![]() имеет минимум?
имеет минимум?
+: Ни при каком х
-: -2
-: 4
-: 0
I:
S:
При каком значении х функция
![]() имеет минимум?
имеет минимум?
-: 1
+: 5
-: Ни при каком х
-: 3
I:
S:
При каком значении х функция
![]() имеет максимум?
имеет максимум?
-: 0
-: 4
+: Ни при каком х
-: 2
I:
S:
При каком значении х функция
![]() имеет минимум?
имеет минимум?
-: Ни при каком х
-: -4
+: 0
-: 4
I:
S:
При каком значении х функция
![]() имеет максимум?
имеет максимум?
+: Ни при каком х
-: -4
-: 0
-: 4
I:
S:
При каком значении х функция
![]() имеет максимум?
имеет максимум?
-: Ни при каком х
+: -3
-: 3
-: 1
V2: Точки перегиба. Интервалы вогнутости, выпуклости
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
-:
![]()
+:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
-:
![]()
+:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
-:
![]()
+:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
+:
![]()
-:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
-:
![]()
+:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
+:
![]()
-:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
+:
![]()
-:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
+:
![]()
-:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
-:
![]()
+:
![]()
-:
![]()
I:
S:
Функция
![]() является вогнутой на интервале
является вогнутой на интервале
-:
![]()
+:
![]()
-:
![]()
V1:Дифференциальное исчисление функции нескольких переменных
V2: Частная производная
I:
S: Частная
производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
![]() равна…
равна…
-:-1
-: 2
+:1
-:0
I:
S: Частная
производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
![]() равна…
равна…
-:-1
-: 4
+:-4
-: 0
I:
S: Частная
производная функции
![]() по
переменной х в точке
по
переменной х в точке
![]() равна…
равна…
-: -1
-: 3
+: -3
-: 0
I:
S: Частная
производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
![]() равна…
равна…
-: -1
-: 0,5
+:1
-: 0
I:
S: Частная
производная функции
![]() по
переменной х в точке
по
переменной х в точке
![]() равна…
равна…
-: -0,5
-: 0,5
+: 3
-: 0
I:
S: Частная
производная функции
![]() по
переменной х в точке
по
переменной х в точке
![]() равна…
равна…
-: – 0,5
-: 0,5
+: 4
-: -4
I:
S: Частная
производная функции
![]() по
переменной у в точке
по
переменной у в точке
![]() равна…
равна…
-: -0,5
-: 0,5
+: 1
-: -1
I:
S: Частная
производная функции
![]() по
переменной у в точке
по
переменной у в точке
![]() равна…
равна…
-: -2
-: 0,5
+: 5
-: 0
I:
S: Частная
производная функции
![]() по
переменной х в точке
по
переменной х в точке
![]() равна…
равна…
-: -2
-: 0,5
+: 0
-: 7
I:
S: Частная
производная функции
![]() по
переменной х в точке
по
переменной х в точке
![]() равна…
равна…
-: -8
-: 0,5
+: 0
-: 4
I:
S: Частная
производная функции![]() по
переменной у в точке
по
переменной у в точке
![]() равна…
равна…
-: -2
-: 4
+: 6
-: 1
I:
S: Частная
производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
![]() равна…
равна…
-: 3
+: 1,5
-: 1
-: 0,5
I:
S: Частная
производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
![]() равна…
равна…
-: е
-: 2е
+: 3е
-: 3
I:
S: Частная
производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
![]() равна…
равна…
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S: Частная
производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
![]() равна…
равна…
-: – 3
-:
![]()
-: 1
+: 3
I:
S:
Частная производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
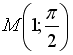 равна…
равна…
-: 1
-: 0
+: – 1
-: 4
I:
S:
Частная производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
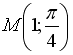 равна…
равна…
-: 0
+: – 2
-: 5
-: 10
I:
S:
Частная производная функции
![]() по
переменной
по
переменной
![]() в
точке
в
точке
![]() равна…
равна…
+:
![]()
-:
![]()
-: 1
-:
![]()
V1: Интегральное исчисление
V2:Основные методы интегрирования
I:
S: Первообразными
функции
![]() являются
…
являются
…
+:
![]()
-:
![]()
+:
![]()
-:
![]()
+:
![]()
I:
S: Первообразными
функции
![]() являются…
являются…
-:
![]()
+:
![]()
+:
![]()
-:
![]()
I:
S: Первообразными
функции
![]() являются…
являются…
-:
![]()
+:
![]()
+:
![]()
-:
![]()
I:
S: Первообразными
функции
![]() являются…
являются…
-:
![]()
+:
![]()
+:
![]()
-:
![]()
I:
S: Первообразными
функции
![]() являются…
являются…
-:
![]()
+:
![]()
-:
![]()
+:
![]()
I:
S:
Первообразными
функции
![]() являются…
являются…
+:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S:
Первообразными
функции
![]() являются…
являются…
-:
![]()
+:
![]()
+:
![]()
-: -7cos7x
I:
S:
Первообразными
функции
![]() являются…
являются…
+:
![]()
-:
![]()
+:
![]()
-: -2cos9x
I:
S:
Первообразными
функции
![]() являются…
являются…
+:
![]()
+:
![]()
-:
![]()
-: 84sin12x
I:
S:
Первообразными
функции
![]() являются…
являются…
+:
![]()
+:
![]()
-:
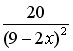
-:
![]()
V2:Интегрирование рациональных дробей
I:
S: Установите соответствие между неопределенными интегралами и разложениями подынтегральных функций на элементарные дроби.
L1:
![]()
R1:
![]()
L2:
![]()
R2:
![]()
L3:
![]()
R3:
![]()
L4:
![]()
R4:
![]()
R5:
![]()
I:
S: Установите соответствие между неопределенными интегралами и разложениями подынтегральных функций на элементарные дроби.
L1:
![]()
R1:
![]()
L2:
![]()
R2:
![]()
L3:
![]()
R3:
![]()
L4:
![]()
R4:
![]()
R5:
![]()
I:
S: Установите соответствие между неопределенными интегралами и разложениями подынтегральных функций на элементарные дроби.
L1:
![]()
R1:
![]()
L2:
![]()
R2:
![]()
L3:
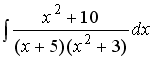
R3:
![]()
