2012_MATAN-2 / 2012 МАТАН-2 / 2012 ПРАКТИКА / ПРАКТИКА №7 Геометрические приложения определённого интеграла

2

Практическое занятие:

Тема: Геометрические приложения определённого интеграла.

Площадь фигуры , равна .

Площадь фигуры , равна .

Если фигура ограничена кривой, заданной параметрическими уравнениями ,, прямыми , и осью , то её площадь равна , где и определяются из уравнений , ( на отрезке ).

Площадь криволинейного сектора , , где - полярные координаты, равна .

В задачах 7.235-7.238 вычислить площади фигур, ограниченных линиями, заданными в прямоугольных координатах:

7.235 а) , ; б) , ; в) , .

7.236 а), ; б), ; в) , , , .

7.237 а) , , ; б) ,; в) , , , , .

7.238 а) , ; б),; в) , , .

В задачах 7.240-7.243 вычислить площади плоских фигур, ограниченных линиями: а) заданными параметрически; б) заданными в полярных координатах.

7.240 а) (астроида); б) , (окружности).

7.241 а) (эллипс) и ; б) (трилистник) .

7.242 а) (циклоида) и ; б) (кардиоида)

7.243 а) (кардиоида); б) (лемниската).

7.244 Найти площадь фигуры, ограниченной лемнискатой и окружностью ).

Длина дуги плоской кривой , равна

Длина дуги плоской кривой, заданной параметрическими уравнениями ,, , равна .

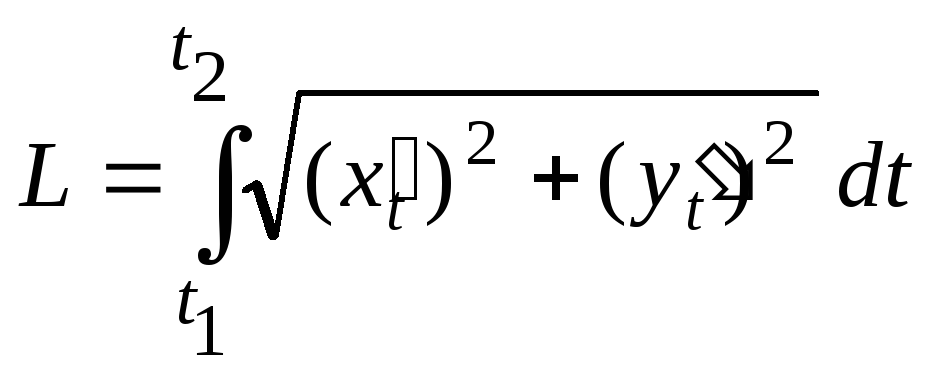В задачах 7.246-7.249 найти длины дуг следующих кривых:

7.246 а) ; б) (астроида).

7.247 а) ; б)

7.248 а) ; б) (циклоида)

7.249 а) ; б) ;

Объём тела, образованного вращением вокруг оси плоской фигуры , равен .

Объём тела, образованного вращением вокруг оси плоской фигуры ,, равен .

Объём тела, образованного вращением вокруг оси фигуры , , равен .

В задачах 7.255-7.260 вычислить объемы тел, полученных вращением плоской фигуры Ф , ограниченной указанными линиями вокруг: а) оси ; б) оси .

7.255 Ф: . 7.256 Ф: .

7.257 Ф: . 7.258 Ф: .

ОТВЕТЫ:

7.235 а) б) в) . 7.236 а) б) в). 7.237 а) б) в) . 7.238 а) б) в) . 7.240 а) б) 7.241 а) б) 7.242 а) б) 7.243 а) б) 7.244 7.246 а) б) 7.247 а) б) 7.248 а) б) 7.249 а) б) 7.251 а) ; б) ; в) . 7.252 а) ; б) ; в) . 7.253 а) ; б) ; в) . 7.255 , . 7.256 , . 7.257 , . 7.258 , .