Лабораторная работа № 2.10 Исследование температурной зависимости удельного сопротивления меди и кремния

Цель работы:

• наблюдение температурной зависимости удельного сопротивления меди и кремния;

• определение величины температурного коэффициента сопротивления меди на основе опытных данных;

• определение энергии активации кремния с помощью опытных данных.

Приборы и оборудование: специальная установка, омметр, соединительные проводники.

Краткие теоретические сведения

1.1. Электрический ток в металлах и полупроводниках

По своей способности проводить электрический ток твёрдые тела подразделяются на проводники, диэлектрики и полупроводники.

Для количественной характеристики электрических свойств тел используют физические величины: проводимость проводника, а также сопротивление проводника. Материал, из которого изготовлены элементы цепи, оценивают с помощью физических величин: удельная электрическая проводимость и удельное сопротивление проводника.

Сила тока I, текущего по однородному цилиндрическому проводнику постоянного сечения, пропорциональна падению напряжения U на проводнике:



где – сопротивление однородного цилиндрического проводника (Ом) длиной L (м) и с постоянным поперечным сечением S (м²),  – удельное сопротивление вещества, из которого изготовлен проводник (Ом·м), – проводимость проводника (), – удельная электрическая проводимость вещества ().

В проводнике удельная электрическая проводимость, а также удельное сопротивление могут меняться от точки к точке, поскольку они характеризуют электрические свойства вещества, заключённого в физически бесконечно малом объёме вокруг рассматриваемой точки проводника. Среди твёрдых тел наименьшей удельной электрической проводимостью обладают изоляторы (диэлектрики). Значения удельной проводимости диэлектриков лежат в диапазоне от до. Наибольшей удельной проводимостью обладают твёрдые тела, относящиеся к группе проводников. Удельная электрическая проводимость металлов лежит в пределах отдо.

1.2. Температурная зависимость электропроводности металлов и полупроводников

С изменением температуры удельная проводимость металлов и полупроводников меняется по-разному. С понижением температуры удельная проводимость металлов возрастает и для чистых металлов стремится к бесконечности при стремлении температуры проводника к абсолютному нулю. По мере роста температуры удельная проводимость металлов убывает. Увеличение сопротивления металлического проводника электрическому току с ростом температуры объясняется увеличением интенсивности колебательного движения ионов кристаллической решётки проводника, препятствующего направленному перемещению электронов проводимости в образце.

Зависимость сопротивления металлического проводника от температурыt (в °С) в широком интервале температур можно считать линейной

,

где – сопротивление проводника при 0 °С, – температурный коэффициент сопротивления проводника ().

У полупроводников наблюдается иная, чем у металлов, температурная зависимость электропроводности.

При понижении температуры удельная электрическая проводимость полупроводника убывает. При температурах, близких к абсолютному нулю, полупроводник ведёт себя подобно диэлектрику. При увеличении температуры образца удельная проводимость полупроводников, начиная с некоторой температуры, сравнима с удельной проводимостью металлов. Такое поведение удельной проводимости полупроводника связано с увеличением числа носителей тока при возрастании температуры образца. При комнатной температуре сопротивление полупроводника с хорошей точностью определяется следующей формулой

,

где – сопротивление полупроводникового образца при абсолютной температуреT (в К); A – некоторый коэффициент, характеризующий свойства данного образца и слабо зависящий от температуры, – постоянная Больцмана,E – энергия активации полупроводника.

Пользуясь формулой , можно найти энергию активации E, которая определяется следующим выражением

.
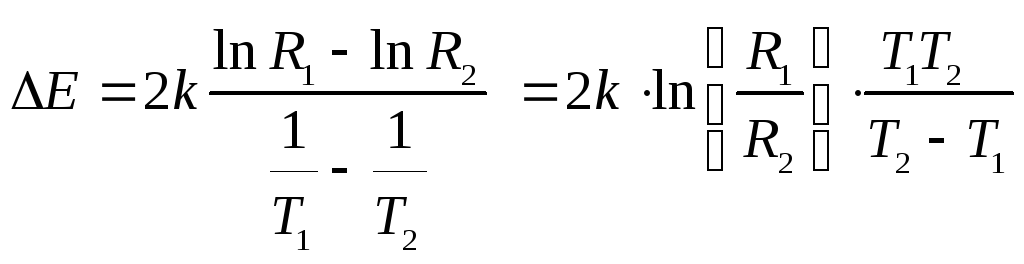