Построение графика функции с условием

Функция может быть задана разными формулами на разных участках изменения аргумента. При задании функции можно использовать условную функцию.

Пример 3.2

Пример 3.2

Построить график функции Y(x), заданной следующим образом:

Y=ln(x), x>0

Y=1/x, x<=0

Используем условную функцию if(cond, x, y)

Условная функция возвращает x , если условие cond есть true, возвращает y, если условие есть false. Условий может быть несколько.

На графике (Рис.3.8) нанесена риска x=0

,

,

Рис. 3.8. Листинг построения графика примера 3.2

Условную функцию удобно использовать при построении области определения функции. Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. С помощью условной функции можно показать график области допустимых значений .

Пример 3.3

Пример 3.3

Построить область определения функции

Ведем функцию

тогда

Область допустимых значений

Строим функцию S(x), используя условную функцию

Строим график функции S(x) (Рис.3.9)

Рис. 3.9. Листинг построения графика примера 3.3

Построение графика функции для табулированных значений

Часто бывает необходимо построить график по точкам. Для этого аргумент и функция вводятся как индексные переменные от номера точки, номер точки – ранжированная переменная.

Пример 3.4

Пример 3.4

Построить график функции по 15 точкам, x меняется от 0 до 1,5 с шагом = 0,1:

, ,

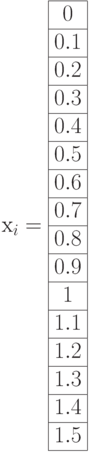
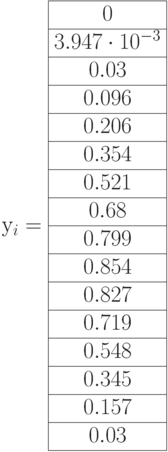
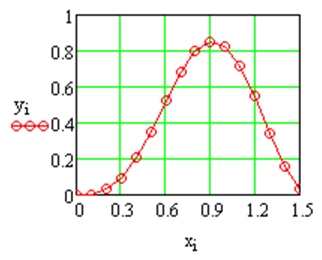
Рис. 3.10. Листинг построения графика примера 3.4

• Ввести номер точки i как ранжированную переменную.

• Ввести xi как с индексную переменную. Ввести функцию с индексом 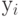. Построить таблицы значений аргумента и функции в виде вектор-столбцов.:

• Построить график, подставляя индексные переменные (Рис.3.10).

Можно ввести x и y, как векторы. В этом случае на графике в соответствующих ячейках указываются только имена переменных (Рис.3.11).

, ,

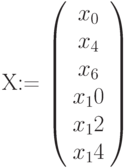
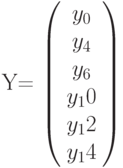
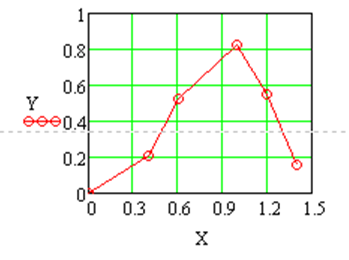
Рис. 3.11. Листинг построения графика примера 3.4. На графике введены точки как значения векторов

Графики функции, заданной параметрически

В ряде случаев для задания функций используются параметрически заданные уравнения. Например, пусть функции x=x(t), y=y(t), непрерывны при t из (a, b) и устанавливают зависимость (x,y) точки плоскости от значения параметра t. Таким образом, задается на плоскости кривая в параметрической форме. Х=f1(t) и у=f2(t).

Пример 3.5

Пример 3.5

Построить график функции, заданной в виде:

при

В случае построения графика параметрически заданной кривой в шаблоне функции необходимо указать y(h), вместо независимой переменной x под осью абсцисс необходимо соответственно задать x(h) (Рис.3.12).

, ,

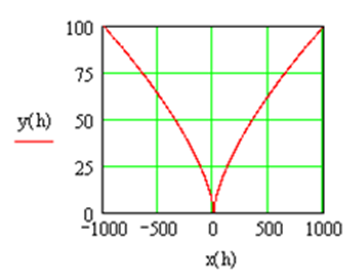
Рис. 3.12. Листинг построения графика примера 3.5

Графики в полярных координатах

В MathCAD полярные графики рисуются с использованием стандартных преобразований и. Предполагается, что r имогут принимать и положительные, и отрицательные значения. Типичный полярный график показывает зависимость выражения для радиуса от угла.

Построение графика

Полярный график строится с использованием шаблона полярного графика на панели Графика. Выражение для функции и угла вводятся в соответствующие шаблоны графика. Можно построить несколько графиков на одном и том же чертеже. Все выражения должны использовать одну и ту же переменную. Угол вводится в радианах (по умолчанию) или в градусах (указываются единицы – deg).

• Определить 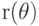как функцию,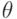

• заполнить шаблоны,

• отобразить график в полярных координатах (Рис.3.13).

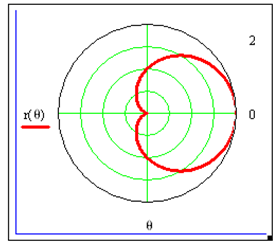
Рис. 3.13. График в полярных координатах. В шаблонах для радиуса: r: (0;2)