38)Циліндричні поверхні. Циліндри.

Циліндричною називається поверхня, що утворена переміщенням прямої (твірної) вздовж деякої заданої лінії (напрямної) паралельно заданому напряму.

Будемо розглядати циліндричні поверхні, напрямні яких знаходяться в одній з координатних площин, а твірні паралельні координатній осі, що перпендикулярна цієй площині.

Нехай у площині 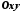міститься деяка лінія, рівняння якої має вигляд:

(1.5)

Побудуємо циліндр з твірними, паралельними осі , і напрямною.

Теорема. Рівняння циліндра з твірними, паралельними осі , має вигляд (1.5), тобто не містить координати.

Доведення. Візьмемо на циліндрі будь-яку точку . Вона знаходиться на деякій твірній. Нехайє точкою перетину цієї твірної з площиною. Отже, точказнаходиться на лініїі її координати задовольняють рівняння (1.5). Але точкамає ті ж самі абсцису і ординату, що і точка. Таким чином, рівнянню (1.5) задовольняють і координати точки, тому що воно не містить, і оскільки 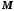– це будь-яка точка циліндра, то рівнянням циліндра буде рівняння (1.5).

Аналогічно, рівняння 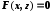є рівнянням циліндра з твірними, паралельними осі , ає рівнянням циліндра з твірними, паралельними осі . Назва циліндра визначається назвою напрямної. Якщо напрямною єеліпс

(1.6)

у площині , то відповідна йому циліндрична поверхня називаєтьсяеліптичним циліндром (рис. 1.7). Його рівняння співпадає з рівнянням еліпса (1.6).

Частинним випадком еліптичного циліндра є круговий циліндр, який визначається рівнянням

. (1.7)

Рівняння

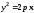(1.8)

визначає параболічний циліндр (рис 1.8), а рівняння

(1.9)

визначає гіперболічний циліндр (рис 1.9).

39)Лінійчасті поверхні. Дати означення квадратичної форми і записати її матрицю.

Означення 4. Квадратичною формою називається многочлен від n змінних , в якому повний степінь коженого одночлена дорівнює двом.

Приклад.

Числова функція f(x,x) одного векторного аргумента x, яка отримується з білінійної форми f(x,y) при x = y є квадратичною формою від координат вектораx.

В загальному випадку квадратичная форма має вигляд:

Квадратичній формі співставляється симетрична матриця

яка називається матрицею квадратичної форми. Легко бачити, що матриця А збігається з матрицею симетричної білінійної форми, з якої отримується дана квадратична форма. Позначимо через - стовпчик, що складається зі змінних. Тоді

=

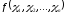Ранг матриці квадратичної форми А називаєься рангом відповідної квадратичної форми

40)Канонічний вигляд квадратичної форми.

Нехай тоді канонічний вигляд квадратичної форми буду таким:

   (4.21)

   Приведемо без доведення дві теореми про канонічний вигляд квадратичної форми ( доведення цих теорем див., наприклад, в підручнику Д.В.Беклемишева. Курс аналитической геометри и линейной алгебры ).

   Теорема 1. Для кожної квадратичної форми існує базис, в якому вона має канонічний вигляд.

   Теорема 2. (закон інерції квадратичних форм). Число додатних і від’ємних коефіцієнтів в канонічному вигляді квадратичної форми не залежить від вибору базису, в якому вона приведена до канонічного вигляду.