
- •1)Поняття прямокутної матриці. Види матриць.
- •2) Лінійні операції над матрицями
- •3)Добуток матриць
- •9) Системи алгебраїчних лінійних рівнянь. Матрична форма запису лінійної системи.
- •11)Матричний метод
- •12)Поняття вектору. Лінійні операції над векторами.
- •14)Довжина вектора та відстань між двома відрізками.
- •16)Обчислення площі паралелограма, побудованого на двох неколінеарних векторах. Умова колінеарності двох векторів.
- •17)Мішаний добуток, його властивості та обчислення.
- •18)Обчислення об’єму паралелепіпеду, побудованого на трьох не компланарних векторах. Умова компланарності двох векторів.
- •19)Різні типи рівнянь прямої на площині.
- •20)Відхилення та відстань точки від прямої
- •21)Кут між прямими на площині.
- •22) Умови паралельності та перпендикулярності прямих на площині.
- •23)Різні типи рівнянь площини.
- •24)Відхилення та відстань точки від площини.
- •29)Лінії другого порядку(коло, еліпс, гіпербола, парабола)
- •30)Загальне рівняння ліній другого порядку.
- •31)Системи координат у просторі.
- •32)Площина у просторі.
- •33)Поверхні другого порядку.
- •34)Загальне рівняння поверхні другого порядку.
- •35)Сфера, еліпсоїд.
- •36)Гіперболоїди, параболоїди.
- •37)Конічні поверхні. Конус.
- •38)Циліндричні поверхні. Циліндри.
- •39)Лінійчасті поверхні. Дати означення квадратичної форми і записати її матрицю.
- •40)Канонічний вигляд квадратичної форми.
- •41)Означення знаковизначених квадратичних форм.
- •44)Закон інерції для квадратичних форм.
- •46)Метод Лагранжа зведення квадратичної форми до канонічного вигляду.
- •47)Критерії Сільвестра.
- •49)Поняття тензора. Компоненти тензорів та їх перетворення.
- •52)Додавання та множення тензорів. Згортання тензорів. Властивість симетрії тензорів. Перестановка індексів, симетрування та альтернування. Сложение тензоров
- •54)Векторне поле. Циркуляція векторного поля. Дивергенція та ротор векторного поля. Векторные поля
- •Циркуляция векторного поля
- •Дивергенция и ротор векторного поля
- •55) Теорема Гаусса-Остроградського. Теорема Стокса. Диференціювання вектора за напрямом. Векторне формулювання теорем Гаусса-Остроградського і Стокса.
33)Поверхні другого порядку.
Еліпсоїд
![]()

Сфера
![]()

Однополий гіперболоїд
![]()

Однополий гіперболоїд обертання
![]()

Двополий гіперболоїд
![]()

Двополий гіперболоїд обертання
![]()
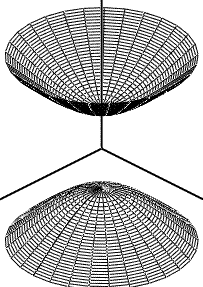
Конус


Конус обертання
![]()

Еліптичний параболоїд
![]()

Параболоїд обертання
![]()

Гіперболічний параболоїд


Еліптичний циліндр
![]()

Гіперболічний циліндр
![]()

Параболічний циліндр
![]()

34)Загальне рівняння поверхні другого порядку.
Поверхня другого порядку - геометричне місце точок,декартові прямокутні координатияких задовольняють рівняння виду
a 11 x 2 + a 22 y 2 + a 33 z 2 + 2 a 12 x y + 2 a 23 y z + 2 a 13 x z + 2 a 14 x + 2 a 24 y + 2 a 34 z + a 44 = 0
в якому принаймні один з коефіцієнтів a 11 , a 22 , a 33 , a 12 , a 23 , a 13 відмінний від нуля.!
35)Сфера, еліпсоїд.
Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением
![]()
где a, b, c>0 — параметры эллипсоида. Это уравнение называется каноническим уравнением эллипсоида, а система координат, в которой эллипсоид описывается каноническим уравнением, называется канонической.
В частном случае a = b = c = R имеем уравнение сферы
![]()
36)Гіперболоїди, параболоїди.
Канонічне рівняння параболоїда в декартових координатах:
![]()
якщо a і b мають один знак, то параболоїд зветься еліптичним.
якщо a і b мають різні знаки, то параболоїд зветься гіперболічним.
якщо один з коефіціентів дорівнює нулю, то параболоїд зветься параболічним циліндром.
Еліптичний параболоїд
Еліптичний параболоїд виглядає як овальна чашка й може мати точку максимуму або мінімуму. У системі координат з трьома осями x, y і z, еліптичний параболоїд може бути поданий рівнянням
![]()
Гіперболічний параболоїд
Гіперболічний параболоїд (не плутати з гіперболоїдом) — це двічі лінійчата поверхня, що має вигляд сідла. У підходящій системі координат гіперболічний параболоїд може бути поданий рівнянням
![]()
Гіперболо́їд — вид поверхні другого порядку в тривимірному просторі, що задається в Декартових координатах рівнянням
![]() (Однопорожнинні
гіперболоїд),
(Однопорожнинні
гіперболоїд),
де a і b - дійсні півосі, а c - уявна піввісь;
або
![]() (Двопорожнинні
гіперболоїд),
(Двопорожнинні
гіперболоїд),
де a і b - уявні півосі, а c - дійсна піввісь.
Якщо a = b, то така поверхня називається гіперболоїдом обертання. Однопорожнинні гіперболоїд обертання може бути отримати обертаннямгіперболи навколо її уявної осі, двопорожнинний - навколо дійсної.
 гіперболоїд
гіперболоїд
37)Конічні поверхні. Конус.
Поверхня,
яка утворена прямими лініями, що проходять
через задану точку
 і перетинають задану плоску лінію
і перетинають задану плоску лінію (яка не проходить через
(яка не проходить через ),
називаєтьсяконічною
поверхнею
або конусом.
Лінія
),
називаєтьсяконічною
поверхнею
або конусом.
Лінія
 називаєтьсянапрямною
конуса,
точка
називаєтьсянапрямною
конуса,
точка
 – їївершиною,
а пряма, яка описує поверхню – твірною.
– їївершиною,
а пряма, яка описує поверхню – твірною.
Нехай
напрямна
 задана рівняннями
задана рівняннями
 ,
(1.10)
,
(1.10)
а
точка
 є вершиною конуса (рис. 1.4).
є вершиною конуса (рис. 1.4).
Візьмемо
на поверхні конуса будь-яку точку
 (рис. 1.4). Твірна, яка проходить через
точки
(рис. 1.4). Твірна, яка проходить через
точки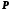 і
і перетинає напрямну
перетинає напрямну у деякій точці
у деякій точці .
Координати точки
.
Координати точки задовольняють рівнянням (1.10) напрямної,
тобто
задовольняють рівнянням (1.10) напрямної,
тобто
 .
(1.11)
.
(1.11)
Канонічні
рівняння твірних, що проходять через
точки
 і
і мають вигляд
мають вигляд
 .
(1.12)
.
(1.12)
Рівняння
конічної поверхні отримаємо після
виключення
 і
і з рівнянь (1.11) і (1.12). Наприклад, якщо
вершина конуса розташована в точці
з рівнянь (1.11) і (1.12). Наприклад, якщо
вершина конуса розташована в точці ,
а напрямною є еліпс
,
а напрямною є еліпс , який лежить в площині
, який лежить в площині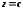 ,
то рівняння (1.11) і (1.12) відповідно мають
вигляд
,
то рівняння (1.11) і (1.12) відповідно мають
вигляд і
і .
Виключаючи з них
.
Виключаючи з них і
і з урахуванням того, що
з урахуванням того, що ,
отримаємо рівняння конуса
,
отримаємо рівняння конуса .
.
Поверхні, що утворені рухом прямої, отримали назву лінійчатих, а прямі, що їх складають, називаються прямолінійними твірними. Серед поверхонь другого порядку лінійчатими є циліндричні і конічні поверхні, а також однопорожнинний гіперболоїд і гіперболічний параболоїд.\
Ко́нус — геометричне тіло, отримане шляхом об'єднання всіх променів, що виходять з однієї точки — вершини конуса, і таких що проходять через довільну плоску поверхню.
