23)Різні типи рівнянь площини.

Загальне рівняння площини

Будь-яку площину можна задати рівнянням площини першого ступеня вигляду

A x + B y+ C z + D = 0

де A, B і C не можуть одночасно дорівнювати нулю.

Рівняння площини в відрізках

Якщо площина перетинає осі OX, OY і OZ в точках з координатами (a, 0, 0), (0, b, 0) і (0, 0, с), то вона може бути знайдена, якщо використати формулу рівняння площини в відрізках

x	+	y	+	z	= 1
a		b		c

Рівняння площини, що проходить через точку, перпендикулярно вектору нормалі

Щоб скласти рівняння площини, за координатами точки площини M(x₀, y₀, z₀) і вектора нормалі площини n = {A; B; C}можна використати наступну формулу.

A(x - x₀) + B(y - y₀) + C(z - z₀) = 0

Рівняння площини, що проходить через три задані точки, які не лежать на одній прямій

Якщо задані координати трьох точок A(x₁, y₁, z₁), B(x₂, y₂, z₂) і C(x₃, y₃, z₃), які лежать на площині, то рівняння площини можна знайти за наступною формулою

x - x1	y - y1	z - z1	= 0
x2 - x1	y2 - y1	z2 - z1
x3 - x1	y3 - y1	z3 - z1

24)Відхилення та відстань точки від площини.

Відхилення точки від площини заданої нормованим рівнянням

, Якщо і початок координат лежать по різні сторони площини, в протилежному випадку. Відстань від точки до площини дорівнює

Відстань від точки, До площини, заданої рівнянням, Обчислюється за формулою:

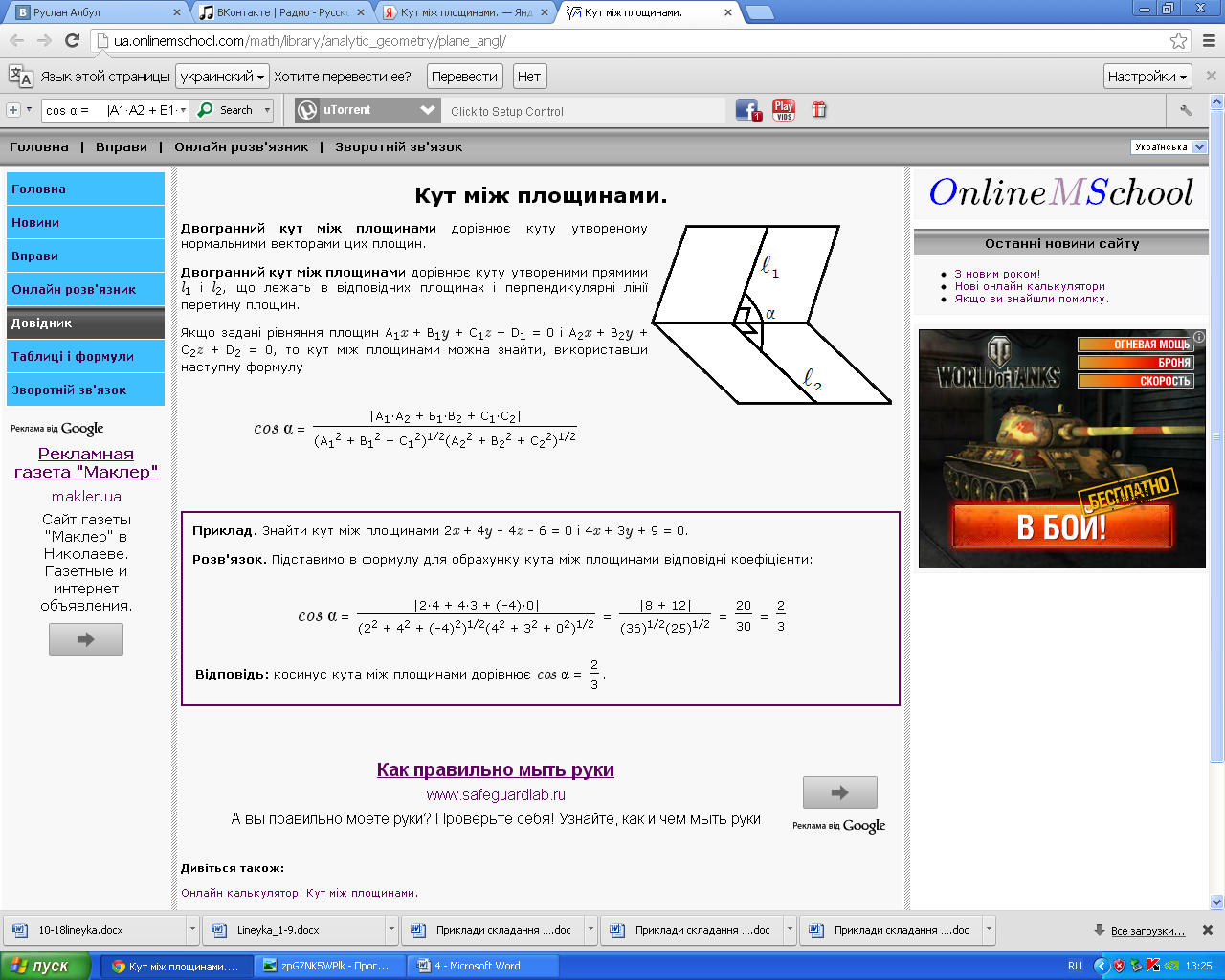
25)Кут між площинами.

Двогранний кут між площинами дорівнює куту утвореними прямими l₁ і l₂, що лежать в відповідних площинах і перпендикулярні лінії перетину площин.

Якщо задані рівняння площин A₁x + B₁y + C₁z + D₁ = 0 і A₂x + B₂y + C₂z + D₂ = 0, то кут між площинами можна знайти, використавши наступну формулу

26)Канонічне та параметричне рівняння прямої в просторі.

Канонічне рівняння прямої в просторі

Якщо відомі координати точки A(x₀, y₀, z₀), що лежить на прямій і напрямного вектора n = {l; m; n}, то рівняння прямої можна записати у каноничному вигляді, якщо використати наступну формулу

Параметричне рівняння прямої в просторі

Параметричне рівняння прямої може бути записане наступним чином

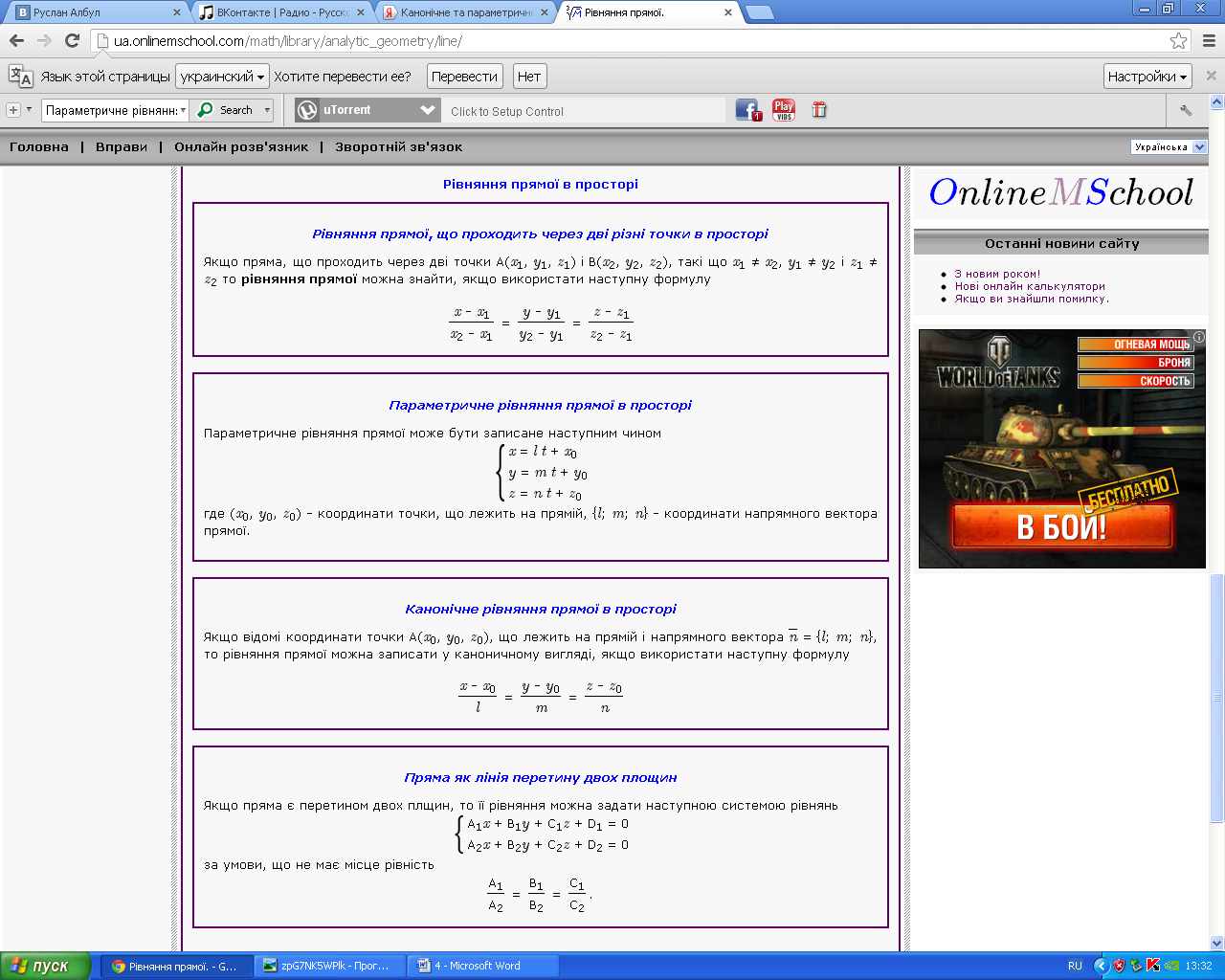
где (x₀, y₀, z₀) - координати точки, що лежить на прямій, {l; m; n} - координати напрямного вектора прямої.

27)Пряма як перетин двох площин.

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

28)Геометричнмй зміст лінійних нерівностей з двома змінними.

Якщо вираз F(x, у) є лінійним, тобто F(x, у) = Ax + By + С, де А, В, С - сталі, то ми маємо лінійне рівняння

Ax + By + С = 0, (2-40)

та дві лінійні нерівності

Ах + Ву + С < 0, (2-41)

Ax + By + С > 0. (2-42)

Якщо коефіцієнти А і В не дорівнюють одночасно нулю, то рівнян-ня (2.40) визначає на площині пряму а нерівності (2.41) і (2.42) -відповідно дві півплощини, на які пряма (2.40) розбиває всю коор-динатну площину. Для того щоб з’ясувати, яка із цих двох півпло-щин визначається заданою лінійною нерівністю, можна застосувати, наприклад, такий спосіб.

Виберемо яку-небудь точку, підставляємо її координати в нерівність, що перевіряється.

Якщо координати точки задовольняють нерівність, то нерівність визначає ту площину в якій знаходиться вибрана точка; якщо ж координати точки не задовольняють нерівність, то нерівність визначає площину, яка не містить вибраної точки.