
Економетрика
.docx
Варіант 25
Завдання 27. Моделі, які зводяться до моделі множинної лінійної регресії. Приклади застосування простої лінійної регресії.
Економетрика – це галузь економічної теорії, яка вивчає моделі економічних систем у формі, що уможливлює перевірку цих моделей на адекватність засобами математичної статистики. Мета економетрики – здійснювати емпіричну перевірку положень економічної теорії, підтверджуючи чи відхиляючи останні.
За допомогою моделі простої лінійної регресіїї ми вивчали зв’язок між залежною змінною y та незалежною змінною x. Так, наприклад, при дослідженні попиту нас цікавить залежність обсягу попиту на деякий товар від ціни на цей товар, цін на взаємозамінні з даним товари та від доходів споживачів. При наявності n спостережень модель множинної лінійної регресії записується у вигляді
y=β0 xi0 + β1xi1 +…+ β k-1 xi,k-1 + ε1
де xij– значення j-ї незалежної змінної (xj) в i-му спостереженні, збурення εi задовольняють тим самим припущенням, що і в моделі простої регресії. 1. Нульове середнє: Eεi = 0,i = 1n .
2. Рівність дисперсій: Dεi = Eεi2= σ2= const,i = 1n, .
3. Незалежність збурень: εі та εj незалежні при i ≠ j .
4. Незалежність збурень та регресорів: xij та εі незалежні для всіх i та j (якщо регресори не стохастичні , то дане припущення виконується автоматично).
5. (Додаткове). Збурення εi нормально розподілені для всіх i.
Моделі, які зводяться до моделі множинної лінійної регресії.
Розглянемо виробничу функцію Коба–Дугласа:
Y = ALα Cβ (1)
де Y–валовий випуск, L–обсяг трудових ресурсів, С–обсяг капіталу (виробничих фондів), A, α, β – параметри. Коефіцієнт пропорційності A відображає рівень технології. Парамери α та β є коефіцієнтами еластичності відносно праці та капіталу (отже, функція Коба–Дугласа є виробничою функцією зі сталою еластичністю). Прологарифмувавши рівняння (1), маємо:
y = a + αl + βc (2)
де a = lnA, l = lnL, c = lnC. Якщо ввести до рівняння (2) стохастичний доданок, то одержимо модель лінійної регресії:
y = a + αl + βc +ε. (3)
Щоб перетворити вихідну модель (1) на стохастичну, обчислимо експоненту від обох частин рівності (3):
Y = ALα Cβ eε . (4)
Ми бачимо, що модель (4) можна звести до моделі лінійної регресіі. Аналогічно можна вивчати досить широкий клас моделей, які за допомогою перетворень змінних та рівнянь можна звести до моделі лінійної регресії. Широковживаним є приклад поліноміальної регресії:
y= β0+ β1x+ β1x2+…+ β k-1xk-1+ ε.
Приклади застосування простої лінійної регресії.
Припустимо, що існують дві змінні x i y, де x - незалежна змінна (регресор), y - залежна змінна. Співвідношення між цими змінними позначимо: y = f (x). Будемо розрізняти детерміновані і статистичні співвідношення. При статистичному співвідношенні кожному значенню x відповідає не єдине значення y, але залежну змінну y можливо точно описати у імовірнісних термінах. Припустимо, що функція f(x) лінійна за x, тобто f(x) = α + βx, а співвідношення між x та y є статистичним, а саме
yi = α + βx + ε (1.1)
де доданок ε називається збуренням або похибкою і має відомий імовірносний розподіл (тобто є випадковою величиною). В рівнянні (1.1) α + βx є детермінованим компонентом, збурення ε є випадковим або стохастичним компонентом; α і β називаються регресійними коефіцієнтами або параметрами регресії, які потрібно оцінити на основі даних про x та y.
Приклад.
В Таблиці 1.1. наведено обсяги сукупного доходу у розпорядженні та сукупного споживання для США у постійних доларах 1972 р. Дані з Таблиці 1.1. зображено графічно на Рис.1.3. З графіка видно, що точки, які відповідають спостереженням, розташовані навколо деякої прямої, отже доцільно розглянути лінійну функцію споживання. Оцінимо її за допомогою моделі простої лінійної регресії:
yi = α + βxi + εi , i=1,10
де через xi та yi позначено відповідно рівень доходу і споживання в році 1969 + i (наприклад i = 5 відповідає 1974 року). Спочатку обчислимо


x =(751,6+779,2+810,3+864,7+857,5+874,9+906,8+942,9+988,8+1015,7)/10 = =879,24;
y =(672,1+696,8+737,1+767,9+762,8+779,4+823,1+864,3+903,2+927,6)/10 =
= 793,43;
Sxx = ((751,6 – 879,24)2 + (779,2 – 879,24)2 + (810,3 – 879,24)2 + + (864,7 – 879,24)2 + (857,5 – 879,24)2 + (874,9 – 879,24)2 + + (906,8 – 879,24)2 + (942,9 – 879,24)2 + (988,8 – 879,24)2 + + (1015,7879,24)2 ) = 67192,4;
Syy = ((672,1 – 793,43)2 + (696,8 – 793,43)2 + (737,1 – 793,43)2 + + (767,9 – 793,43)2 + (762,8 – 793,43)2 + (779,4 – 793,43)2 + + (823,1 – 793,43)2 + (864,3 – 793,43)2 + (903,2 – 793,43)2 + + (927,6 – 793,43)2 ) = 64972,1;
Sxy = ((751,6 – 879,24) (672,1 – 793,43) + (779,2 – 879,24) (696,8 – 793,43) +
+ (810,3 – 879,24) (737,1 – 793,43) + (864,7 – 879,24) (767,9 – 793,43) + (857,5 – 879,24) (762,8 – 793,43) + (874,9 – 879,24) (779,4 – 793,43) + (906,8 – 879,24) (823,1 – 793,43) + (942,9 – 879,24) (864,3 – 793,43) + (988,8 – 879,24) (903,2 – 793,43) + (1015,7879,24) (927,6 – 793,43) ) = 65799,3.
За
формулами
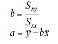 знаходими оцінки методу найменших
квадратів коефіцієнгів моделі yi
= α + βxi
+
εi:
знаходими оцінки методу найменших
квадратів коефіцієнгів моделі yi
= α + βxi
+
εi:
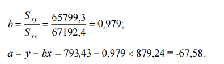
Отже, рівняння вибіркової регресійної прямої (рівняння фунцції споживання) має вигляд:
y = – 67,58 + 0,979x.(1.2)
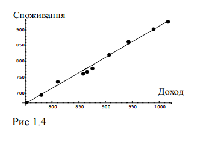
Графік цієї прямої зображено на Рис. 1.4. разом з фактичними даними. Щоб мати уявлення про тісноту зв’язку між доходом і споживанням, обчислимо коефі- цієнт детемінації. За формулою
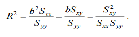
Маємо: R2 = bSxy/Syy = 0.979×65799,3/64972,1 = 0.990702.
Як ми бачимо, зв’язок між споживанням і доходом є вельми тісним. Перед тим, як використовувати рівняння (y = – 67,58 + 0.979x) для економічного аналізу або побудови прогнозів, модель (yi = α + βxi + εi ,i = 1,10,) потрібно перевірити на адекватність. Перевіримо гіпотезу про значущість регресії двома способами. Спочатку використаємо F-статистику
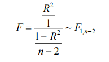
Маємо:
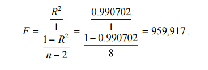
Нехай, рівень значущості α дорівнює 0,05. Критичне значення F кр = 5,32. Ми бачимо, що |F|≥Fкр, отже гіпотеза про рівність β нулю відхиляється, тим самим модель (yi = α + βxi + εi ,i = 1,10) є значущою. Обчислимо стандартні похибки оцінок. Спочатку знайдемо суму квадратів залишків RSS.
RSS = Syy – b2 Sxx = 64972,1 – 0.9792 ×67192,4 = 537,0.
Далі знаходимо оцінку дисперсії збурень
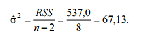
Стандартна похибка b дорювнює:

Перевіримо
гіпотезу про те, що коефіцієнт нахилу
регресійної прямої β
дорівнює нулю за допомогою t-статистики
перевірки гіпотез(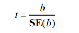 ):
):
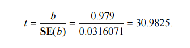
Нехай, рівень значущості α дорівнює 0,05. Критичне значення tкр = 2,306. Ми бачимо, що |t|≥tкр, отже гіпотеза відхиляється. Отже, ми можемо вважати модель адекватною.
З теорії споживання відомо, що коефіцієнт нахилу лінійної функції споживання є маргінальною або граничною схильністю до споживоння. Таким чином, ми встановили, що в середньому 0.979×100 = 97,9% прирісту доходу витрачається на споживання). Обчислене значення граничної схильності до споживання знаходиться в інтервалі (0; 1), що узгоджується з економічною теорією.
Завдання 57. Міри точності прогнозів.
Розробка прогнозу вимагає оцінки його точності та надійності. Точність і надійність прогнозів – широко поширені в прогностичній літературі терміни, сенс яких, як це уявляється на перший погляд, цілком очевидний. Проте зміст цих термінів часто тлумачиться достатньо суб'єктивно.
Про точність прогнозу прийнято судити по розміру помилки прогнозу - різниці між прогнозним і фактичним значенням досліджуваної змінної. Проте такий підхід до оцінки точності можливий тільки в двох випадках. По-перше, коли період попередження вже закінчився, і дослідник має фактичні значення змінної. При короткостроковому прогнозуванні це цілком реально. По-друге, коли прогноз розробляється, тобто прогнозування здійснюється для деякого моменту часу в минулому, для котрого вже є фактичні дані. При цьому наявна інформація ділиться на дві частини. Одна з них, що охоплює більш ранні дані, служить для оцінювання параметрів прогностичної моделі, а більш пізні дані розглядаються як реалізації відповідних прогностичних оцінок. Отримані ретроспективно помилки прогнозу якоюсь мірою характеризують точність застосованої методики прогнозування і можуть виявитися корисними при зіставленні декількох методів. У той же час, розмір помилки ретроспективного прогнозу не можна розглядати як остаточний доказ придатності, або навпаки, непридатності застосовуваного методу прогнозування. До неї варто ставитися з відомою обережністю і при її застосуванні в якості міри точності необхідно враховувати, що вона отримана при використанні лише частини наявних даних. Проте ця міра точності має більшу наочність і теоретично більш надійна, ніж похибка прогнозу, обчислена для періоду, характеристики котрого вже були використані при оцінюванні параметрів моделі. У останньому випадку похибки, як правило, будуть незначними і мало залежні від теоретичної обґрунтованості, застосованої для прогнозування моделі.
У зв'язку з перевіркою точності прогнозів необхідно зробити ще одне зауваження. Так, якщо для ретроспективного прогнозування застосовується модель, що містить одну або декілька екзогенних змінних, то точність прогнозу буде значною мірою залежати від того, наскільки точно визначені значення цих змінних на період попередження. При цьому можливі два шляхи: скористатися фактичними значеннями екзогенних змінних (так званий прогноз ex post) і очікуваними їхніми значеннями (так званий прогноз ex ante). Природно, що точність прогнозу ex post, що, як правило, і одержують при перевірці, буде вище, ніж точність прогнозу ex ante, тому що в першому випадку буде виключений вплив похибки у значеннях екзогенних змінних.
Перевірка точності одного прогнозу мало що може сказати досліднику. Гарний одиничний прогноз може бути отриманий і по поганій моделі, і навпаки. Звідси випливає, що про якість прогнозів застосовуваних методик і моделей можна судити лише по сукупності зіставлень прогнозів і їхньої реалізації.
Найбільш простою мірою якості прогнозів за умови, що є дані про їхню реалізацію, може стати відносне число випадків, коли фактична реалізація охоплювалася інтервальним прогнозом, до загального числа прогнозів.
Ефективність методу прогнозування залежить від багатьох чинників. На практиці дослідник має досить велику свободу вибору не тільки типу моделі, але і кількості введених до неї параметрів. Виділяють такі критерії:
1) кількість зусиль, що витрачаються на побудову моделі і наявність готових машинних програм;
2) швидкість, із яким метод уловлює істотні зміни у поведінці ряду, наприклад, раптовий зсув математичного сподівання або збільшення кута нахилу лінії тренду;
3) існування серійної кореляції у помилках;
4) незмінюваність первинних даних;
5) повний обсяг роботи в деяких сферах діяльності - тисячі рядів щомісяця потребують оновлення, невеликі витрати і швидкість мають першорядне значення;
6) терміновість прогнозування.
Практика розробки різноманітного роду прогнозів спирається на цілу систему методів, серед яких статистичні методи прогнозування займають важливе місце. Вирішальну роль у статистичному підході до прогнозування грає вибір відповідної моделі, що, будучи наповненої числовими параметрами, стає безпосереднім інструментом прогнозування – предиктором. Володіючи предиктором, можна одержати варіанти прогнозу, що відповідають визначеним гіпотезам і умовам, врахованим при його побудові. Мета статистичної моделі - не замінити судження і досвід спеціаліста, а дати йому в руки інструмент, що дозволяє більш глибоко проникнути в сутність досліджуваних явищ, інструмент, у якому специфічним чином узагальнена і зведена у систему різноманітна статистична інформація. Одержувані на основі предикторів прогнози мають сенс тільки в рамках тих умов, гіпотез і припущень, що були враховані при розробці відповідних статистичних моделей і при їхньому застосуванні для прогнозування. Таким чином, розробка і застосування моделей у прогностичних цілях припускають поглиблений економіко-статистичний аналіз досліджуваного об'єкта.
