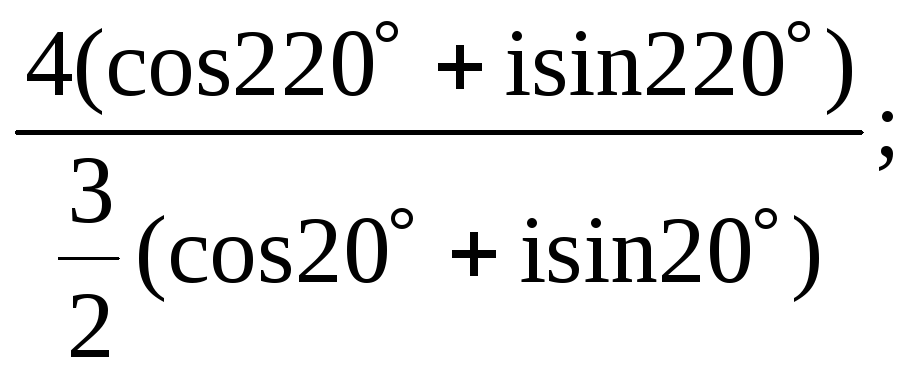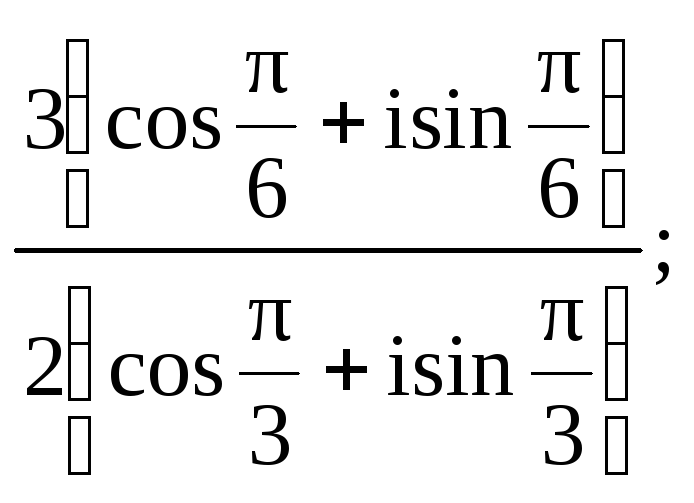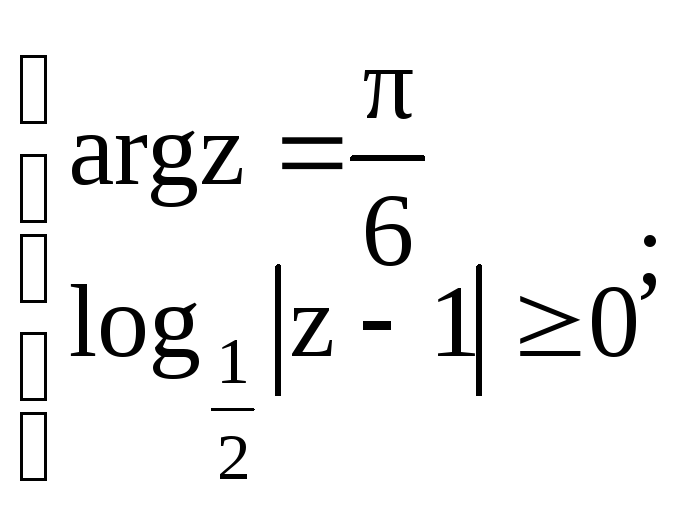§ 11 Аналитическое задание множеств

на комплексной плоскости

1) Re z = a (или х = а) – уравнение вертикальной прямой

(Re z = 0 – уравнение мнимой оси);

2) lm z = b (или y = b) – уравнение горизонтальной прямой

(lm z = 0 – уравнение действительной оси);

3) Re z > a (Re z < a) – полуплоскость, лежащая справа (слева) от прямой Re z = a (рисунки 15, 16).

Например, Re z > 0 (рисунок 17);

Рисунок 15 Рисунок 16 Рисунок 17

4) Im z > b (Im z < b) – полуплоскость, лежащая сверху (снизу) от прямой Im z = b (рисунки 18, 19).

Например, Im z  0 (рисунок 20).

Рисунок 18 Рисунок 19 Рисунок 20

5) z – z₀ = R – окружность с центром в точке z₀, радиусом R. Например, z = R – окружность с центром в точке О;

6) z - z₀ < R (z – z₀ > R) – круг радиусом R с центром в точке z₀ (внешность такого же круга) (рисунки 21, 22);

Например, z 1 – круг с центром в точке (0; 0), радиусом R с его границей (рисунок 23);

7) arg (z – z₀) = -луч, выходящий из точки z₀ под углом  к положительному лучу (рисунок 24).

arg z =  – аналогичный луч, выходящий из точки z = 0 (рисунок 25);

Рисунок 21 Рисунок 22 Рисунок 23

Рисунок 24 Рисунок 25

8)  < arg (z – z₀) <  – угол с вершиной в точке z₀, стороны которого составляют с положительным лучом углы  и  (рисунок 26).

Например,  < arg z <  – угол с вершиной в точке (0; 0), стороны которого составляют с положительным лучом углы  и  (рисунок 27).

Рисунок 26 Рисунок 27

Пример 11.1 Изобразить на комплексной плоскости множество всех точек, для которых:

а) lm z > 2; б)z + 2 = 2; в) z + 3 - i > 2;

г)

Решение:

а) если z = x + iy, то lm z = y. Неравенство можно записать в виде y > 2 (рисунок 28).

Рисунок 28 Рисунок 29

б)

. Множество точек, удовлетворяющих данному уравнению лежит на окружности с центром в точке (-2; 0) и радиусом 2 (рисунок 29).

в)

Это все точки, которые лежат вне окружности с центром в точке (– 3; 1) и радиусом 2 (рисунок 30).

Рисунок 30 Рисунок 31

г) данная система равносильна следующей (рисунок 31):

.

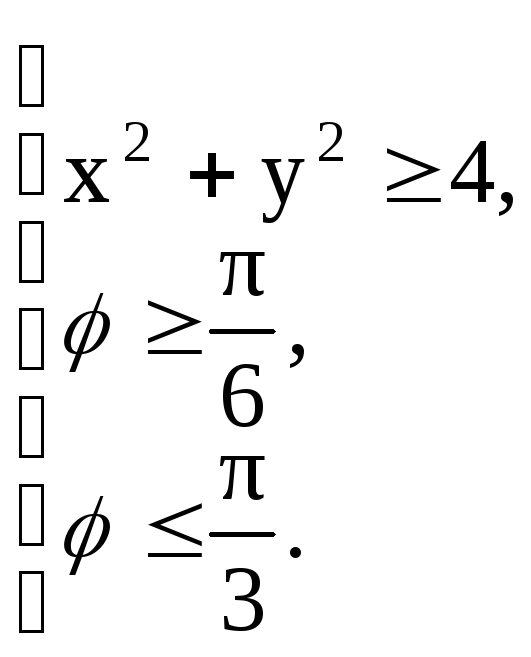Упражнения

14 Представить числа в тригонометрической форме:

а) –4 +4i; б);

в) ;.

15 Выполнить действия. Результат записать в тригонометрической форме:

а)	б)
в)	г)

16. Выполнить действия. Результат записать в алгебраической форме:

а)	б)
в)	г)

д)

17 Вычислить, используя формулу Муавра. Результат записать в алгебраической форме:

а) (1 – i)30;	б)
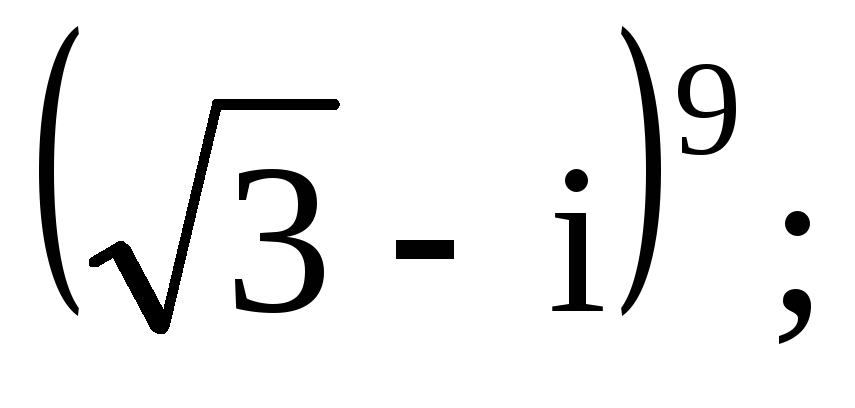
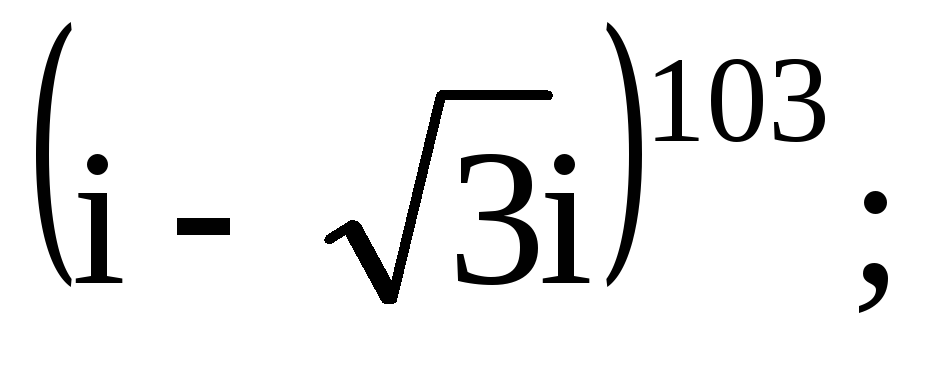
в)	г)
д)	е)
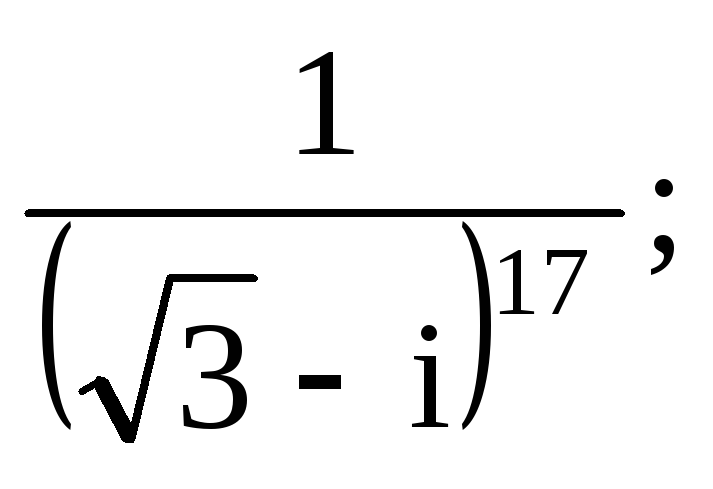
ж)	з)
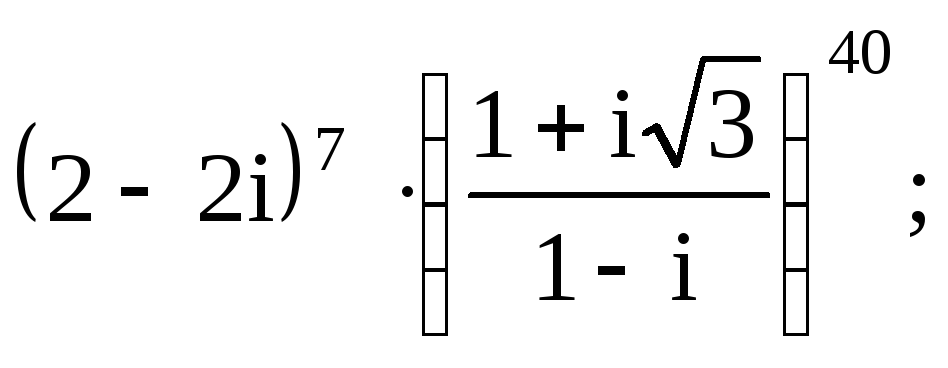
и)

18 Изобразить на комплексной плоскости множество точек, для которых:

а)	б)	в)
г)	д)	е)
ж)

19 Вычислить корни, а результат изобразить на комплексной плоскости:

а) б)

20 Решить уравнение:

а) z⁴ – 16 = 0; б) i - z⁵ = 2;

в) 2z⁶ + 5 = 0; г)

21 Решить уравнение:

а) z² + z + 5 = 0; б) 2z² – 3z + 4 = 0;

в) z² – (2 + 3i) + z + 4i – 2 = 0; г) z² – 3z + 3 + i = 0;

г) 16z⁴ + 4 z² + 1 = 0; д) z² + (5 + 5i)z + 2 + 11i = 0.