Введение

Основная цель предмета «Высшая математика» для технического колледжа – это выработка у учащихся и студентов умений и навыков математического анализа прикладных задач, связанных с их профессиональной деятельностью. Материал темы «Комплексные чис-ла» востребован при изучении таких предметов, как «Теоретические основы электротехники», «Теоретическая механика», «РЭС и комп-лексы» и др.

Настоящее учебно-методическое пособие адресовано студентам всех специальностей колледжа и предназначено для индивидуальной и самостоятельной работы студентов. Оно может быть востребовано и для аудиторной работы при проведении практических занятий.

Материал темы в пособии разбит на параграфы. Каждый параграф содержит: теоретический материал, примеры решения задач, упражнения для практической и самостоятельной работы студентов. Изучать учебный материал следует в той последовательности, которая приведена в пособии.

Для обобщения и закрепления материала по теме студенты выполняют индивидуальное домашнее задание (ИДЗ), варианты которого приведены в работе. Вариант ИДЗ совпадает с порядковым номером студента в учебном журнале. Сроки выполнения ИДЗ определяет преподаватель.

Для отлично успевающих студентов предлагаются дополнительные задания повышенной сложности.

§1 Определение комплексного числа

Пара чисел является упорядоченной, если указано, какое из чисел пары является первым и какое – вторым. Пары чисел (a; b) и (b; a), если b ≠ a, считаются различными.

Определение. Комплексным числом называется упорядоченная пара (x; y) действительных чисел x и y, если на множестве этих пар определены понятия равенства, а также операции сложения и умножения по следующим правилам:

1) (x₁; y₁) = (x₂; y₂) ;

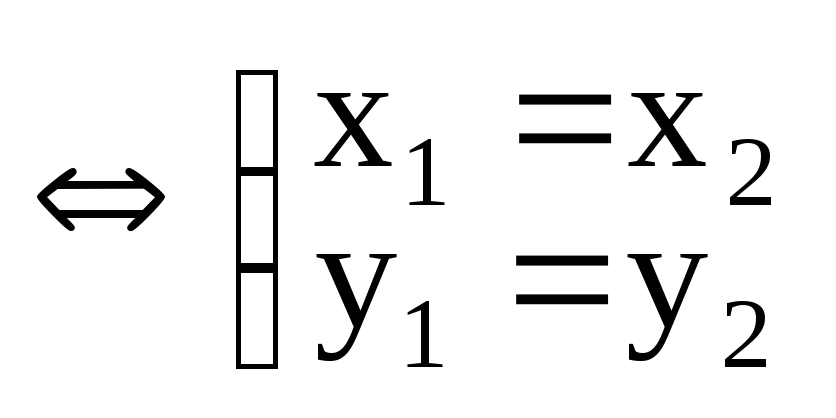2) (x₁; y₁) + (x₂; y₂) = (x₁ + x₂; y₁ + y₂);

3) (x₁; y₁) · (x₂; y₂) = (x₁ x₂ – y₁ y₂; x₁ y₂ + x₂ y₁).

Например,

(3; –6) + (2; 8) = (3 + 2; –6 + 8) = (5; 2);

(3; –6) · (2; 8) = (3 · 2 – ( –6) · 8; 3 · 8 + (–6) · 2) = (54; 12).

Комплексные числа часто обозначают одной латинской буквой, причём обычно используют для этого буквы z и w, иногда с индек­сами, например z₁, z₂, w₀. Равенство z = (x; y) обозначает, что ком­плексное число (x; y) обозначено буквой z. Множество комплексных чисел обозначается С.

§2 Алгебраическая форма записи комплексного числа

Рассмотрим числа вида (х; 0). В результате сложения и умножения таких чисел всегда получаются числа того же вида:

(x₁; 0) + (x₂; 0) = (x₁+x₂; 0);

(x₁; 0) · (x₂; 0) = (x₁·x₂; 0).

Комплексное число (х; 0) отождествляют с действительным чис­лом xи считают (х; 0) = х.

Например, (0; 0) = 0; (2; 0) = 2; (– 5; 0) =– 5; (1; 0) = 1.

Таким образом, множество действительных чисел содержится во множестве комплексных чисел R C.

Отметим, что во множестве Сесть числа, квадрат которых равен отрицательному действительному числу. Это числа вида (0;y):

(0; y) · (0;y) = (–y²; 0) = –y².

Они называютсямнимыми. В частности, число (0; 1) называетсямнимой единицейи для краткости обозначается символомi:

i =(0; 1).

Для этого числа i·i=i²= (0; 1) · (0; 1) = –1. Поэтому числоi(также как и –i= (0; –1)) является корнем уравнения х²+ 1 = 0.

Каждое комплексное число z= (x;y) можно представить в виде

z= (x;y) = (x;y) + (0;y) = (x;y) + (y; 0) · (0; 1) =x+iy.

Запись числа z= (x;y) в видеx+iyназываетсяалгебраической формой комплексного числа. Действительные числа х и у называются соответственнодействительной имнимой частью комплексного числаz=x+iyи обозначаются:

x = Re z = Re(x + iy); y = Im z = Im(x + iy).

Пример 2.1 НайтиRezиImz, если а)z= 1; б)z=i; в)z= 3 – 2i.

Решение.

а) Так как z= 1 = 1 + 0 ·i, тоRe1 = 1, Im1 = 0;

б) z = i = 0 + 1i  Re i = 0, Im i =1;

в) z = 3 – 2i  Re(3 – 2i) = 3, Im(3 – 2i) = –2.

§ 3 Действия над комплексными числами, заданными

в алгеб­раической форме

В результате алгебраических действий над комплексными числами снова получается комплексное число, эти действия производятся по тем же правилам, что и действия над многочленами.

Пусть z₁=x₁+iy₁иz₂=x₂+iy₂.

Правило сложения.При сложении комплексных чисел складыва­ются действительные и мнимые части соответственно.

Пример 3.1 Найти сумму и разность чиселz₁иz₂, гдеz₁= 3 + 2i и z₂= 1 –i.

Решение.

z₁ + z₂ = (3 + 2i) + (1 – i) = 3 + 1 + (2 – 1)i = 4 + i.

z₁ – z₂ = (3 + 2i) – (1 –i) = 3 + 2i – 1 + i = (3 – 1) + (2 + 1)i = 2 + 3i.

Правило умножения. Комплексные числа перемножаются как дву­члены, при этом учитывается, чтоi²= –1.

Пример 3.2 Найти произведение чиселz₁= 1 – 2iиz₂= 3 + 4i.

Решение.

z₁ · z₂ = (1 – 2i)( 3 + 4i) = 1 · 3 + 1 · 4i – 2i · 3 – 2 · 4i² =

= 3 + 4i – 6i + 8 = 11 – 2i.

Правило возведения в степень. Применяется формула бинома Ньютона.

.

Пример 3.3 Найти различные степени числа i, т.е. iⁿ

Решение.

i1 = i;	i2 = –1;	i3 = i2 · i = – i;	i4 = (i2)2 = 1;
i5 = i;	i6 = –1;	i7 = – i;	i8 = 1.

Получаем, для n = 4k, n = 4k + 1, n = 4k + 2, n = 4k + 3 следующие значения:

i^{4k + 1} = i^4k · i = i;

i^{4k + 2} = i^4k · i² = –1;

i^{4k + 3} = i^4k · i³ = –i;

i^4k = (i⁴)^k = 1.

Пример 3.4 Найти i¹⁹⁹⁹.

Решение.

Найдем остаток от деления 1999 на 4:

1999 : 4 = 499 · 4 + 3. Остаток равен 3, поэтому i¹⁹⁹⁹ = i³ = – i.

Пример 3.5 Возвести (2 – i) в третью степень.

Решение.

(2 – i)³ = 2³ – 3 · 2²i + 3 · 2i² – i³ = 8 – 12i – 6 – i = 2 –13i.