§ 8 Алгебраические действия над комплексными

числами в тригонометрической форме.

Формула Муавра

Пусть z₁ = r₁(cos ₁ + isin ₁) и z₂ = r₂(cos ₂ + isin ₂).

Тригонометрическую форму записи комплексного числа удобно использовать для выполнения действий умножения, деления, возведения в целую степень и извлечения корня степени n.

z₁ ∙ z₂ = r₁ ∙ r₂(cos (₁ + ₂) + i sin(₁ + ₂)).

≠0.

При умножении двух комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. При делении их модули делятся, а аргументы вычитаются.

Следствием правила умножения комплексного числа является правило возведения комплексного числа в степень.

z = r(cos  + i sin ).

z ⁿ = r ⁿ(cos n + isin n).

Это соотношение называется формулой Муавра.

Пример 8.1 Найти произведение и частное чисел:

и

Решение

z₁∙z₂∙

= ;

Пример 8.2 Записать в тригонометрической форме число

∙–i)⁷.

Решение

Обозначим и z₂ = – i .

r₁ = |z₁| = √ 1² + 1² = √ 2; ₁ = arg z₁ = arctg;

z₁ = ;

r₂ = |z₂| = √(√ 3)² + (– 1)² = 2; ₂ = arg z₂ = arctg ;

z₂ = 2;

z₁⁵ = ()⁵; z₂⁷ = 2⁷

z = ()⁵ ·2⁷ =

= 2⁹

§ 9 Извлечение корня из комплексного числа

Определение. Корнем n-й степени из комплексного числа z (обо­значают ) называется комплексное число w такое, что wⁿ = z. Если z = 0, то = 0.

Пусть z  0, z = r(cos + isin). Обозначим w = (cos + sin), тогда уравнение wⁿ = z запишем в cледующем виде

ⁿ(cos(n·) + isin(n·)) = r(cos + isin).

Отсюда ⁿ = r,

n·  =  + 2k, k  Z.

Далее ,

 =

Таким образом, w_k = · .

Среди этих значений ровно n различных.

Поэтому k = 0, 1, 2, …, n – 1.

На комплексной плоскос-ти эти точки являются вершинами правильного n-угольника, вписан-ного в окружность радиусом с центром в точке О (рисунок 12).

Рисунок 12

Пример 9.1 Найти все значения .

Решение.

Представим это число в тригонометрической форме. Найдем его модуль и аргумент.

r = .

.

w_k = 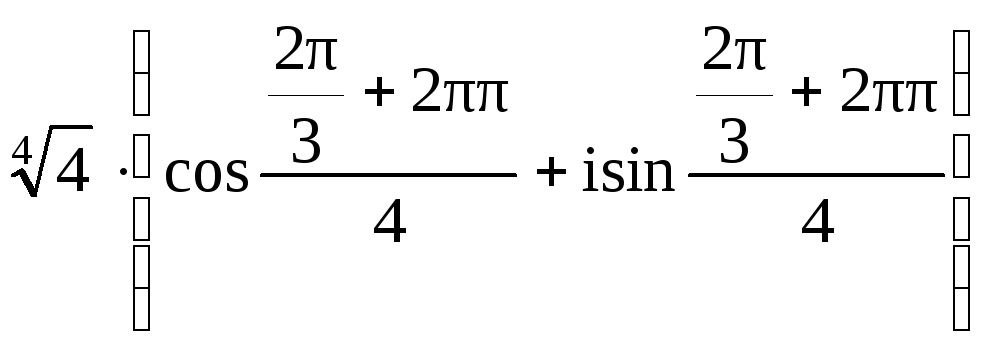, где k = 0, 1, 2, 3.

w₀ = .

w₁ = .

w₂ = .

w₃ = .

На комплексной плоскости эти точки являются вершинами квадрата, вписанного в окружность радиусом с центром в начале координат(рисунок 13).

Рисунок 13 Рисунок 14

Пример 9.2 Найти все значения .

Решение.

z = – 64 = 64(cos +isin);

w_k = , где k = 0, 1, 2, 3, 4, 5.

w₀ = ; w₁ = ;

w₂ = w₃ =

w₄ = ; w₅ = .

На комплексной плоскости эти точки являются вершинами правильного шестиугольника, вписанного в окружность радиусом 2 с центром в точке О (0; 0) – рисунок 14.

§ 10 Показательная форма комплексного числа.

Формула Эйлера

_{Обозначим = cos + isin и = cos - isin. Эти соотношения называются формулами Эйлера.}

_{Функция обладает обычными свойствами показательной функции:}

Пусть комплексное число z записано в тригонометрической форме z = r(cos + isin).

Используя формулу Эйлера, можно записать:

_{z = r ·} .

_{Эта запись называется показательной формой комплексного числа. Используя ее, получаем правила умножения, деления, возведения в степень и извлечения корня.}

_{Если z1 = r1 · и z2 = r2 · ?то}

_{z1 · z2 = r1 · r2 ·} ;

_·

_z ⁿ _{= r} ⁿ _·

_{, где k = 0, 1, … , n – 1.}

_{Пример 10.1 Записать в алгебраической форме число}

_{z = .}

_{Решение.}

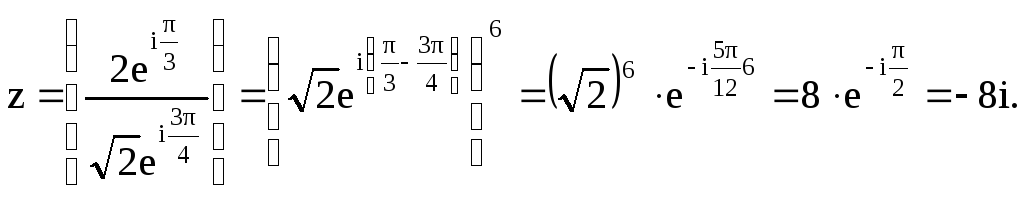
Пример 10.2 Решить уравнение z² + (4 – 3i)z + 4 – 6i = 0.

Решение.

При любых комплексных коэффициентах это уравнение имеет два корня z₁ и z₁ (возможно, совпадающих). Эти корни могут быть найдены по той же формуле, что и в вещественном случае. Так как принимает два значения, отличающихся только знаком, то эта формула имеет вид:

Поскольку –9 = 9 · е^i, то значениями будут числа:

3i и –3i.

Тогда и .

Пример 10.3 Решить уравнения z3 +1 = 0; z3 = – 1.

Решение.

Искомыми корнями уравнения будут значения .

Для z = –1 имеем r = 1, arg(–1) = .

z³ = e^i .

w_k = , k = 0, 1, 2.

w₀

;

Упражнения

9 Представить в показательной форме числа:

a) –1 + i;	в) –5i;
б) 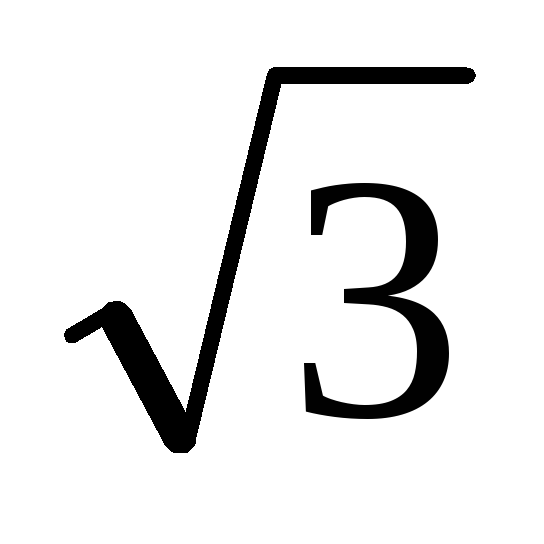+ i;	г) .

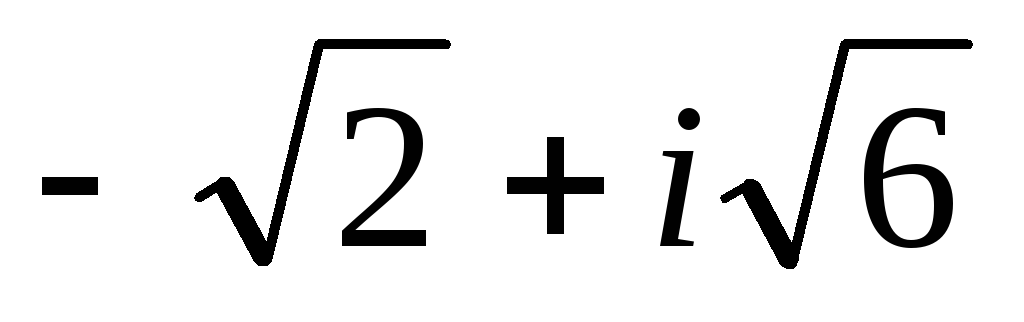10 Записать в показательной и алгебраической формах числа:

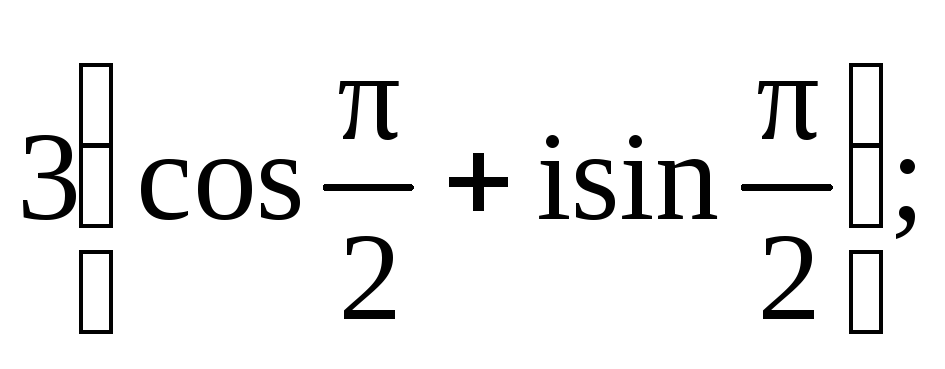
а)	в)
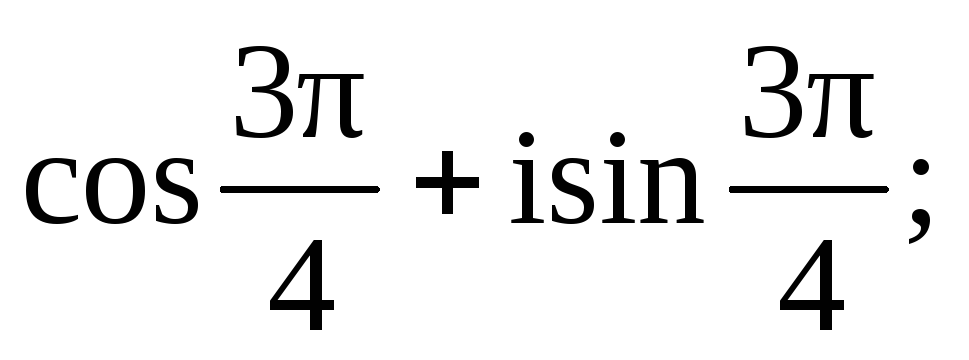
б)	г) 7(cos0 + isin0).

11 Записать в алгебраической и геометрической формах числа:

а)

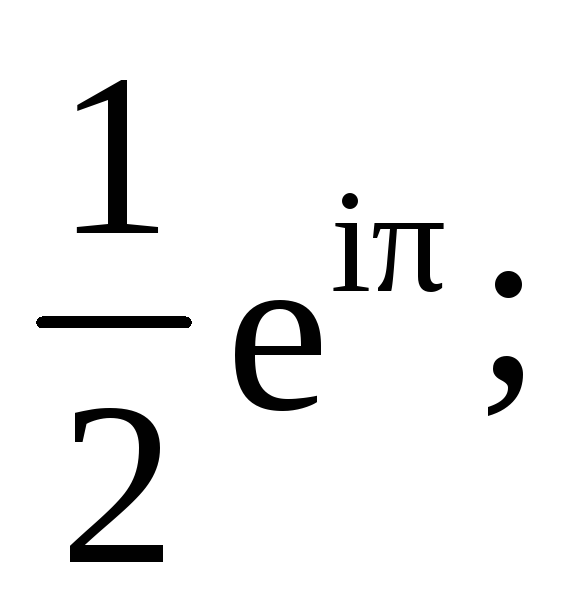
б)

в)

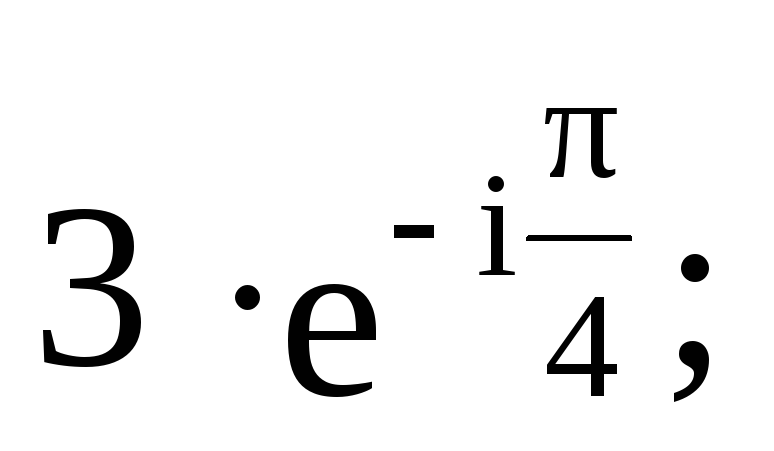
г)

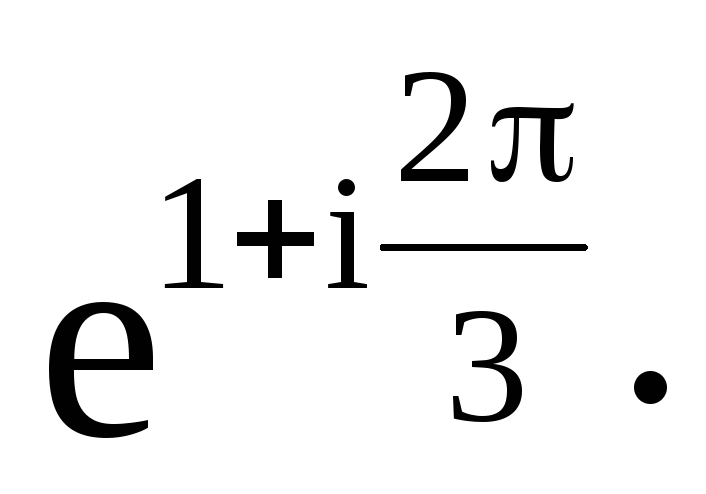
12 Даны числа

Представив их в показательной форме, найти .

13 Используя показательную форму комплексного числа, выполнить действия:

а) б)

в) г)

д)
	.