§ 4 Комплексно-сопряженные числа.

Операция деления

Операция комплексного сопряжения– это изменение знака перед мнимой частью. Еслиz=x+iy, то числоx–iyназывается сопряжен­ным числуzи обозначается :

= = х –iy.

Пример 4.1 Найти числа, сопряженные

а) z₁ = i; б) z₂ = 5; в) z₃ = 1 – 2i; г) z₄ = 7i + 1.

Решение.

а) z₁ = 0 + 1i , то ₁ = –i;

б) z₂ = 5 + 0 · i , то ₂ = 5 – 0 · i = 5;

в) ₃= 1 + 2i;

г) _{4 =} –_{7 i + 1.}

_{Свойства комплексно-сопряженных чисел:}

1) z + = x + iy + x – iy = 2x = 2Re z;

2) z - = x + iy – (x – iy) = 2iy = 2i lm z;

3) z · = (x + iy) (x – iy) = x² + y².

Таким образом, сумма и произведение комплексно сопряженных чисел являются действительными числами, а их разность – число мнимое.

4) = = = x + iy = z С;

5) z =  lm z = 0  ;

6) = ;

7) ;

8) .

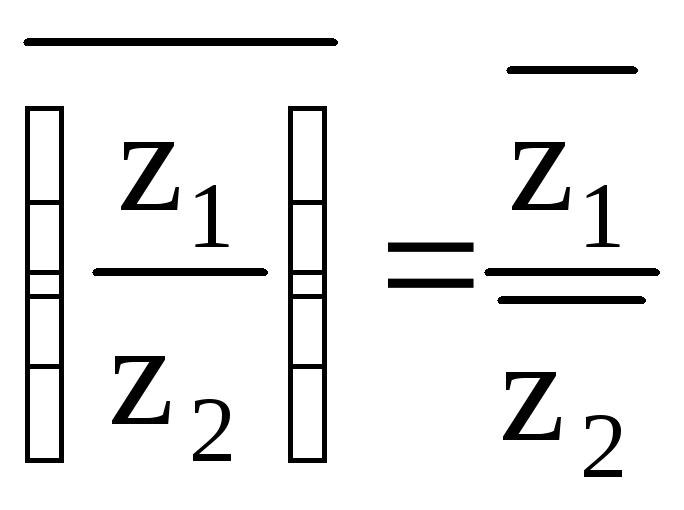Операция деления определяется как действие, обратное умноже­нию. Частное двух комплексных чисел z₁ и z₂  0 – это такое ком­плексное число z, которое удовлетворяет условию z₂ · z = z₁.

Частное получается путем умножения числителя и знаменателя на число , сопряженное знаменателю.

= =

Пример 4.2 Найти , если z₁ = 2 – 5i , z₂ = –3 – 2i .

Решение.

Пример 4.3 Записать в алгебраической форме число

Решение.

Выполняем последовательно все операции:

Re(1 + 2i)² = Re(–3 + 4i) = –3;

(3 – 2i)(5 + i) = 15 + 3i – 10i + 2 = 17 – 7i;

–3 – (17 – 7i) = –3 – 17 + 7i = –20 + 7i;

;

1 + 5i – (4 + i) = 1 + 5i – 4 – i = –3 + 4i;

;

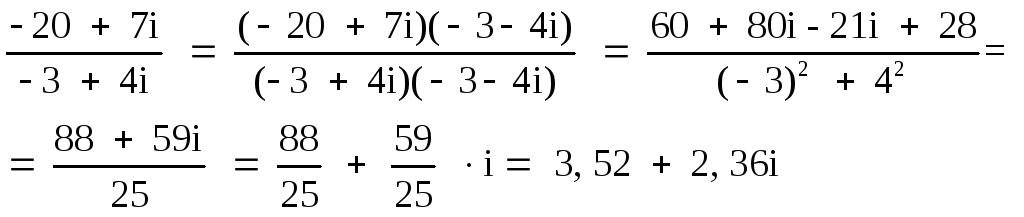
35,2 + 2,36i – (– i) = 3,52 + 2,36i + i = 3,52 + 3,36i.

Упражнения

1 Вычислить:

а) i⁴; i⁸¹; б) в) i²³¹; i²⁰²⁴.

2 Найти число, сопряженное данному:

а) 2i ; –3i; б) (1 + i)(2 + 3i); (2 – i)(3 + i);

в) г) (1 + i)²; (2 – i)².

3 Представить число в алгебраической форме:

а) б)

в) ; г) ;

д) ; е) ;

ж) ; з)

4 Выполнить действия:

а) ; б) ;

в) (1 – i)(4 + 3i)(2 + i)(3 + i) ; г) ;

д) ; е) ;

ж) .

5 Найти значение выражения:

а) z² + 3z + 1 + 3i при z = 2 + 3i;

б) (z – z² + 2z³)(2 – z + z²) при z =.

6 Найти решение уравнений, где x и y – действительные числа:

а) (1 + i) ∙ x + (2 + i) ∙ y = 5 + 3i;

б) 2x + (1 + i)(x + y) = 7 + i;

в) (3 – y + x)(1 + i) + (x – y)(2 + i) = 6 – 3i;

г) (i – z)(1 + 2i) + (1 – iz)(3 – 4i) = 1 + 7i.

§5 Геометрическая интерпретация комплексных чисел

Определение комплексного числа как упорядоченной пары чисел (х; у) позволяет установить взаимно однозначное соответст- вие между комплексным числом

z = x + iy и точкой М(х; у) в декартовой системе координат ОХУ (рисунок 1). Числовую плоскость в этом случае называют комплекс-

Рисунок 1 ной плоскостью.

Ось абсцисс называют действительной осью, а ось ординат – мнимой осью. С другой стороны, комплексное число z = x + iy можно взаимно однозначно поставить в соответствие вектору с координатами х и у и началом в точке О (радиус-вектор). Поэтому понятия "комплексное число", "точка z" и "вектор z" употребляются как синонимы.

Пример 5.1 Изобразить на комплексной плоскости числа

а) z и ; б) z = 1 + 2i.

Решение: а) – рисунок 2; б) – рисунок 3.

Рисунок 2 Рисунок 3