I уровень

1.1. Найдите линейную комбинацию 3A + 2B матриц A и B, если:

1)

2)

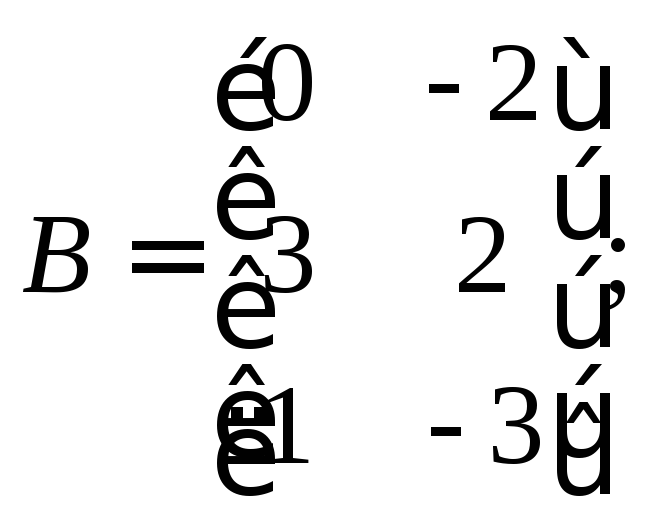
3)

1.2. Вычислите:

1) 2)

3) 4)

1.3. Найдите значения f(A) и f(B) функций f(х), если:

1)

2)

1.4. Приведите матрицу к трапециевидной или треугольной форме:

1) 2)3)

1.5. Пусть Найдите

II уровень

2.1. Найдите сумму, разность и произведение матриц A и B, если:

1)

2)

3)

2.2. Выполните действия:

1)

2)

3)

2.3. Вычислите n-ю степень матрицы, n  N:

1) 2)3)

2.4. Найдите матрицу X из условия

2.5. Найдите если:

1)

2)

2.6. Найдите значение функции f(A), если:

1)

2)

III уровень

3.1. Возведите матрицу в степень:

1) 2)

3) 4)

3.2. Найдите матрицы, коммутативные (перестановочные) с заданной:

1) 2)3)

3.3. Найдите матрицы второго порядка, квадрат которых равен:

1) нулевой матрице; 2) единичной матрице.

3.4. Определите условие, при котором справедливо равенство:

1) 2)

3.5. Для матриц A и B докажите равенство:

1) 2) (A + B)^T = A^T + B^T;

3) (kA)^T = kA^T, где k – число; 4) (AB)^T = B^TA^T.

13.2. Определители, их свойства и вычисление

Каждой квадратной матрице A порядка n можно поставить в соответствие единственное число, которое вычисляется по определенному правилу. Это число называется определителем матрицы A и обозначается |A| или det A, или Δ(A), Δ_А. Порядок матрицы A является и порядком ее определителя. Определители порядка 1–3 вводятся соответственно равенствами:

(13.3)

Минором M_ij элемента a_ij, где называется определитель (n–1)-го порядка, который состоит из элементов матрицы, полученной из данной путем «вычеркивания» i-й строки и j-го столбца.

Алгебраическим дополнением этого же элемента называется число А_ij = (–1)^i+jM_ij. Определитель порядка n, где определяется как число

Последнее равенство называют разложением определителя по элементам первой строки. Оно есть обобщение равенств (13.3).

Свойства определителей

1)

2)

3)

4) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;

5) перестановка двух строк (столбцов) меняет знак определителя на противоположный;

6) |A| = 0, если выполняется одно из следующих условий:

- в определителе есть нулевая строка (нулевой столбец);

- в определителе есть пропорциональные строки (столбцы);

- в определителе есть строки (столбцы), являющиеся линейной комбинацией соответствующих элементов других строк (столбцов);

7) если к элементам одной строки (столбца) определителя прибавить линейную комбинацию соответствующих элементов других строк (столбцов), то значение определителя не изменится.

Основные методы вычисления определителей

1. Для определителей 3-го порядка используют правило треугольников, которое схематично можно изобразить следующим образом:

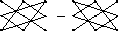
Линии соединяют по три элемента, которые умножаются, а затем произведения складываются.

2. Определитель порядка n может быть вычислен разложением по любой строке (столбцу):

3. Метод эффективного понижения порядка определителя: используя свойства определителя, его преобразуют к такому виду, чтобы все элементы некоторой строки (столбца) определителя, кроме одного, стали нулевыми, затем вычисляют определитель разложением по этой строке (столбцу).

4. Метод приведения к треугольному или диагональному виду с использованием свойств определителя, когда определитель равен произведению диагональных элементов.

Пример 1. Вычислить определитель различными спо­собами.

Решение. 1-й способ. Используем правило треугольников:

2-й способ. Разложим определитель по первой строке:

3-й способ. Занулим элементы первой строки, т. е. используем метод эффективного понижения порядка. Для этого прибавим к элементам 3-го столбца элементы 1-го столбца. Затем разложим определитель по 1-й строке:

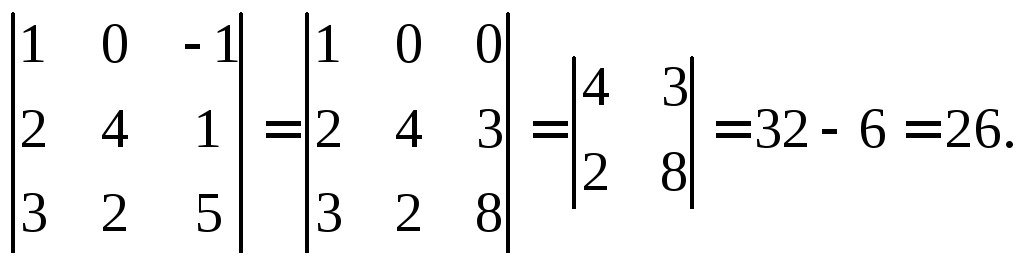
4-й способ. Используя свойства определителя, приведем его к треугольному виду:

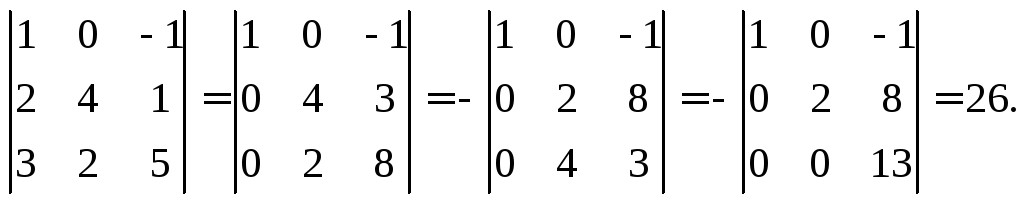
Пример 2. Вычислить определитель

Решение. Используем метод эффективного понижения порядка. Для этого из первой строки вычтем, а ко второй прибавим удвоенную третью строку. Полученный определитель разложим по первому столбцу:

Далее, ко второму столбцу определителя Δ прибавим третий столбец, после чего преобразуем следующим образом: прибавим к первому и третьему столбцам второй столбец, умноженный соответственно на –4 и на –6. В результате получим:

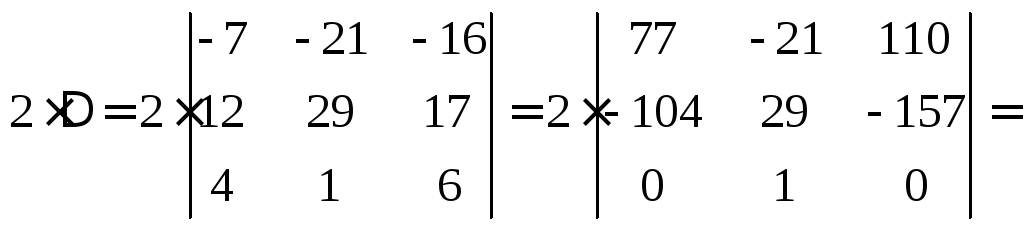
Пример 3. Выяснить, при каких условиях определитель не равен нулю.

Решение. Разложим определитель по 3-й строке:

Значит, , при.

Пример 4. Доказать равенство

Решение. Для доказательства используем метод математической индукции. Проверим справедливость утверждения при n = 1 и 2.

Пусть равенство выполняется при n = k, где k > 2, т. е. Докажем истинность приn = k + 1.

Утверждение доказано методом математической индукции.

Пример 5. Вычислить определитель:

1)

2) где

Решение. 1) Перейдем к алгебраической форме записи всех элементов заданной матрицы: Тогда

2) Вычислим определитель разложением по третьему столбцу:

Поскольку то

Значит,

Задания