I уровень
1.1. Пользуясь определением числовой последовательности, докажите, что:
1)
2)
3)
4)
1.2. Вычислите предел:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
II уровень
2.1. Вычислите предел:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
2.2. Докажите, что последовательность (xn) не имеет предела:
1)
2)
III уровень
3.1.
Задана последовательность
…;
… Найдите
Определите, каким должно бытьn,
для того чтобы разность между
un
и ее пределом по абсолютной величине
не превзошла 10–4.
3.2. Вычислите предел последовательности:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
3.3. Найдите предел последовательности:
1)
если
2)
если
3.4. Вычислите предел числовой последовательности (xn), заданной формулой общего члена, при различных значениях параметров a, b, c:
1)
2)
10.3. Предел функции
Рассмотрим функцию
определенную в некоторой окрестности
точки
(в самой точке
данная функция может быть не определена).
Число
А называется
пределом
функции
в точке
(по Гейне), если для любой последовательности(xn),
сходящейся к
последовательность
соответствующих значений
функции сходится к А.
Обозначают:
или
при
Если функция
в точке
имеет предел, то он единственный.
Если функции
и
имеют пределы в точке
то справедливы формулы:
где С
= const;
(10.3)
(10.4)
(10.5)
(10.6)
Если непосредственное
вычисление предела по формулам
(10.3)–(10.6) приводит к неопределенности
типа
то необходимо вначале тождественно
преобразовать выражение, стоящее под
знаком предела.
Для всех элементарных функций в любой точке их области определения имеет место равенство
(10.7)
которое означает, что операции вычисления предела и функции переставимы.
Кроме предела
функции в точке рассматривают предел
функции на бесконечности:
число A
называется пределом функции
при
(или
),
если для всякой последовательности(xn),
(или
)
при
последовательность
соответствующих значений функции
сходится к числуA.
Обозначают:
Для предела функции на бесконечности также справедливы формулы (10.3)–(10.6).
Функция
называетсябесконечно
малой
функцией при
(или
),
если
Функция
называетсябесконечно
большой
при
если для всякой последовательности(xn),
при
(или
)
последовательность соответствующих
значений функции
является бесконечно большой.
Обозначают:
(10.8)
Если
– бесконечно большая функция при
то она не имеет предела (предел – это
число!). Запись формулы (10.8) следует
воспринимать лишь как обозначение
бесконечно большой функции.
Пример 1.
Пользуясь определением предела функции
по Гейне, доказать, что
Решение.
Пусть (xn)
– произвольная последовательность,
которая сходится к 3
т. е.
Тогда
Пример 2. Вычислить предел функции в точке:
1)
2)
3)
Решение.
1) При непосредственном использовании
формул (10.3)–(10.6) получаем неопределенность
вида
Разложим числитель и знаменатель на множители и сократим дробь на общий множитель. Получим:
2) Непосредственное
вычисление приводит к неопределенности
типа
Для раскрытия приведем выражение в
скобках к общему знаменателю:
Далее разлагаем числитель и знаменатель на множители. Получаем:
3) Непосредственное
вычисление предела при
приводит к неопределенности типа
Умножим числитель и знаменатель на
неполный квадрат суммы выражений
и 2, чтобы в числителе получить разность
кубов:
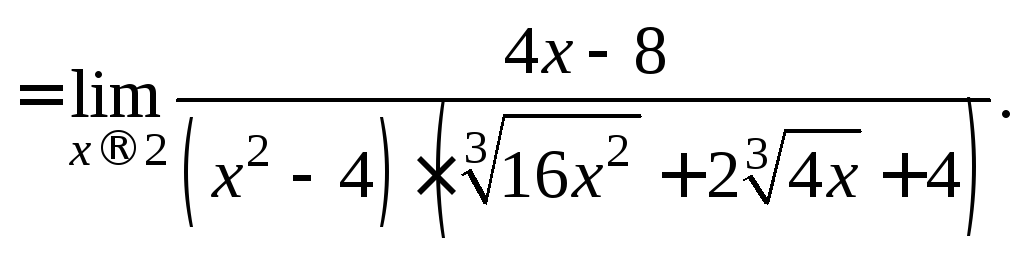
Поскольку
неопределенность типа
сохранилась, разложим многочлены на
множители и сократим:
Переход к пределу
при
дает:
Пример 3.
С помощью вычислений определить, является
ли функция
бесконечно малой или бесконечно большой
при
1)
2)
Решение. 1)
Чтобы ответить на вопрос задачи,
необходимо рассмотреть
Непосредственное
вычисление этого предела приводит к
неопределенности типа
Вынесем в числителе и знаменателе
старшее основание, т. е.
за скобки:
Так как показательная
функция
при
является убывающей, то при
получим:
Тогда, согласно
определению, функция
является бесконечно большой.
2) Вычислим
При
выражение в скобках представляет собой
разность двух бесконечно больших величин
Умножив и разделив функцию на выражение
получим:
В результате
преобразований возникла неопределенность
типа
а поэтому разделим числитель и знаменатель
на старшую степень, т. е. наx.
Получим:
Следовательно, по
определению функция 
является бесконечно малой.
Задания